地球角速度

---

簡介

角速度是一個標量。包含大小和方向的物理量稱為向量量，例如位移、速度等。僅包含大小的物理量稱為標量。例如，距離、速度等。

角速度和角速度都用相同的公式表示，但它們之間唯一的區別是角速度是向量量，而角速度是標量。圓周運動是角運動的一個例子，因為在每個點上，運動物體相對於時間在其每個點上都改變了它們的角。

角運動

如果粒子相對於時間改變其位置，則表示它處於運動狀態。如果粒子的運動沿著直線，則稱為線性運動。如果粒子的運動是沿著圓形路徑，則稱為圓周運動或軌道運動或角運動。地球的自轉、鐵餅投擲、繩子繫住的石頭的運動都是旋轉或角運動的一些例子。因此，角運動定義為任何圍繞固定點運動的物體。

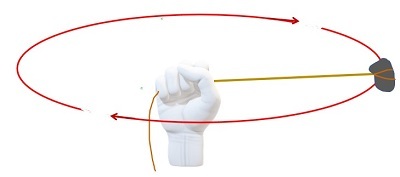
什麼是角速度？

角速度公式：經歷圓周運動的粒子的角速度由它完成路徑的速度決定。角速度是完整旋轉中角度隨時間的變化。它也用符號 ω 表示。

$$\mathrm{ω=\frac{2\pi}{t}}$$

速度是用來了解物體運動快慢的術語。因此，角速度是旋轉物體速度的度量。

角速度單位：弧度每秒。

角速度作為向量場

角速度是在向量場中，它恰好是線性速度 v 的向量場的旋度的值的一半。

$$\mathrm{\overrightarrow{\omega}=\frac{1}{2}(\overrightarrow{
abla}\times \overrightarrow{
u})}$$

角速度公式

角速度由物體在特定時間內完成一次完整旋轉所經過的總角距離計算得出。

$$\mathrm{\overrightarrow{\omega}=\frac{2\Pi}{t}}$$

ω - 角速度

t - 完成一次完整旋轉所需的時間

它也可以透過使用以下公式從線性速度計算得出：

$$\mathrm{
u=r\omega}$$

地球的角速度

我們的地球繞著自己的軸自轉，給我們帶來晝夜交替。地球完成一次完整旋轉所需的時間是 23 小時 56 分 4.09 秒。完整旋轉的角位移為 2π 弧度。

$$\mathrm{角速度=\frac{角位移}{完成一次旋轉所需時間}}$$

為此，時間應轉換為秒。

$$\mathrm{1小時=60分鐘= 3600秒}$$

$$\mathrm{23小時=23×3600=82800秒}$$

$$\mathrm{1分鐘 = 60秒}$$

$$\mathrm{56分鐘=56×60=3360秒}$$

完成一次完整旋轉所需的時間 = 82800 + 3360 + 4.09 = 86164.09

$$\mathrm{角速度=\frac{2\Pi}{86164.09}}$$

$$\mathrm{
u=\frac{6.28}{86164.09}}$$

$$\mathrm{角速度\
u=7.28×10^{-5} 弧度/秒}$$

角速度示例

1. 如果風扇葉片以 16π 弧度/秒的角速度旋轉。它完成一次旋轉需要多少時間？

答：我們知道

$$\mathrm{角速度=\frac{角位移}{時間}}$$

$$\mathrm{\omega=\frac{\theta}{t}}$$

給定

角速度 ω=16Π 弧度/秒

一次旋轉的角位移 = 2π 弧度

$$\mathrm{t=\frac{\theta}{\omega}}$$

$$\mathrm{t=\frac{2\Pi}{16\Pi}}$$

$$\mathrm{t=0.125秒}$$

2. 半徑為 2 米的汽車車輪以每秒 8 米的速度行駛。然後求角速度。

給定

線速度 $\mathrm{
u=8m/s}$

$$\mathrm{r=2m}$$

角速度

$$\mathrm{\omega=\frac{
u}{r}}$$

$$\mathrm{\omega=\frac{8}{2}=4弧度/s}$$

角速度和線速度之間的關係

角速度是根據線速度計算的。

粒子的線速度 $\mathrm{
u=\frac{ds}{dt}}$

粒子的角速度 $\mathrm{\omega=\frac{d\theta}{dt}}$

將方程兩邊乘以 r，我們得到：

$$\mathrm{r\omega=r\frac{d\theta}{dt}\:\:\:\:\:(rd\theta=ds)}$$

$$\mathrm{r\omega=\frac{ds}{dt}}$$

$$\mathrm{r\omega=
u}$$

將速度和角速度聯絡起來的方程是 $\mathrm{
u=r\omega}$

它可以修改為計算角速度為 $\mathrm{\omega=\frac{
u}{r}}$

結論

角速度是一個既有大小又有方向的向量量。如果粒子沿圓形路徑運動，則為圓周運動，物體具有的速度為角速度。角速度或角速度由物體在一分鐘內產生的角位移計算得出。線速度和角速度相互關聯。

常見問題解答

Q1. 赤道處的地球角速度是多少？

答。赤道處地球的速度為 $\mathrm{7.367×10^{-5}\frac{rad}{sec}}$

Q2. 我們如何計算角速度？

答。角速度由物體在特定時間內完成一次完整旋轉所經過的總角距離計算得出。

$$\mathrm{\omega=\frac{2\Pi}{t}}$$

ω - 角速度

t - 完成一次完整旋轉所需的時間

它也可以透過使用以下公式從線性速度計算得出：

$$\mathrm{
u=r\omega}$$

角速度以弧度/秒為單位計算。

Q3. 角速度在所有點都相同。解釋原因？

答。角速度是角運動中單位時間內位移變化率，位移變化率相同。因此，角速度在所有點都相同。

Q4. 描述角速度和角速度。

答。速度是一個標量，因此角速度是對運動物體的標量估計。而角速度是對運動物體的向量估計。角速度指定運動物體的大小和方向。

Q5. 花樣滑冰運動員如何控制他們的角速度？

答。花樣滑冰運動員和芭蕾舞演員在表演時會改變他們的速度。當他們伸展他們的手和腿時，它會增加慣性矩，從而降低角速度。

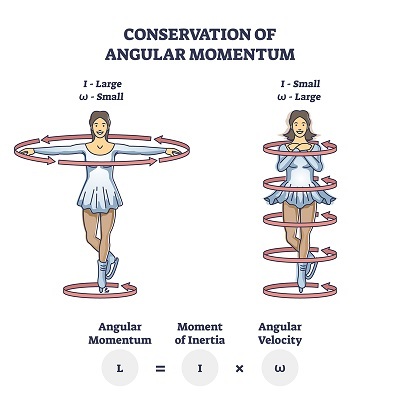
同樣，當他們將手和腿靠近身體時，會減少慣性矩，從而角速度增加。這就是他們在表演過程中控制速度的方式。