角動量——繞固定軸旋轉

---

引言

角動量是旋轉動力學中的一個概念。我們可以將物體的運動分為兩類，即平移運動和旋轉運動。在純平移運動中，物體上的每個點都在一條直線上運動。每個點在給定的時間間隔內移動相同的距離。例如，直線行駛的汽車、在大路上行走的行人等。而在純旋轉中，每個點的運動形成的路徑形成一個圓，其圓心位於旋轉軸上。例如，地球繞其軸自轉、陀螺旋轉等。

對於平移運動，在沒有外力的作用下，我們會發現線性動量總是守恆的。我們稱之為動量守恆定律。我們用它來簡化許多碰撞問題。有人會問，旋轉運動中是否存在這樣的定律？答案是肯定的。在旋轉運動中，我們有角動量守恆定律。角動量是線性動量的角對應值。正如我們所見，我們能夠將它與轉動慣量、力矩和線性動量等其它物理量聯絡起來。

角動量

假設一個質點繞一個軸旋轉，那麼質點繞該軸的動量矩被稱為質點的角動量。

即角動量=線動量×質點的垂直距離

$$\mathrm{\overrightarrow{L}=\overrightarrow{p}\times \overrightarrow{r}}$$

質量為 m 的質點以速度 v 運動，則其線性動量為 L，假設其到旋轉軸的距離由半徑向量 $\mathrm{\overrightarrow{r}}$給出

角動量矢向量表示

$$\mathrm{\overrightarrow{L}= \overrightarrow{r}\times \overrightarrow{p}}$$

$$\mathrm{\lvert\overrightarrow{L} \rvert =rpsin\theta=mvr\:sin\theta}$$

Maschen，角動量定義，標為公有領域，維基百科共享資源上有更詳細的資訊

角動量的單位為 $\mathrm{[ML^2 T^{-1}]}$，國際單位制單位為 $\mathrm{Kg\:m^2 s^{-1}}$。

直角座標系中的角動量

我們還可以在笛卡爾座標中明確寫出角動量。首先，我們以笛卡爾形式寫出 $\mathrm{\overrightarrow{r}}$和 $\mathrm{\overrightarrow{p}}$。

$$\mathrm{\overrightarrow{r}=x\hat{i}+y\hat{j}+z\hat{k}}$$

$$\mathrm{\overrightarrow{p}=p_x\hat{i}+p_y \hat{j}+p_z\hat{k}}$$

$$\mathrm{\overrightarrow{L}=(x\hat{i}+y \hat{j}+z\hat{k})\times (p_x\hat{i}+p_y\hat{j}+p_z\hat{k})}$$

$$\mathrm{\overrightarrow{L}_x=yp_z-zp_y}$$

$$\mathrm{\overrightarrow{L}_y=zp_x-xp_z}$$

$$\mathrm{\overrightarrow{L}_z=zp_y-yp_x}$$

角動量方程的推導

首先，我們來看平移運動和旋轉運動的類似物理量。

量	速度	加速度	力	質量	動量
平移	$\mathrm{\overrightarrow{ u}}$	$\mathrm{\overrightarrow{a}}$	$\mathrm{\overrightarrow{F}}$	$\mathrm{m}$	$\mathrm{\overrightarrow{p}}$
旋轉	$\mathrm{\overrightarrow{\omega}}$ (角速度)	$\mathrm{\overrightarrow{a}}$ (角加速度)	$\mathrm{\overrightarrow{\tau}}$(力矩) =$\mathrm{\overrightarrow{r}\times \overrightarrow{F}}$	I(轉動慣量) = $\mathrm{Σmr^2}$	$\mathrm{\overrightarrow{L}}$(角動量)

表 1: 旋轉運動和平移運動物理量的類比

我們取一個質量為 m 的小質點，其與旋轉軸距離為 $\mathrm{\overrightarrow{r}}$，線性動量為 $\mathrm{\overrightarrow{p}}$。

根據牛頓第二定律，我們有

$$\mathrm{\sum \overrightarrow{F}=\frac{d\overrightarrow{p}}{dt}}$$

我們對這個方程兩邊都與 r 做叉積。

$$\mathrm{\overrightarrow{r}\times \sum \overrightarrow{F}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt}}$$

我們意識到

$$\mathrm{\overrightarrow{r}\times \sum \overrightarrow{F}=\overrightarrow{\tau}}$$

因此

$$\mathrm{\overrightarrow{\tau}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt} ………. (1)}$$

現在我們來看這個式子

$$\mathrm{\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}}$$

因為

$$\mathrm{\overrightarrow{p}=m\overrightarrow{v}\:and\:\frac{d\overrightarrow{r}}{dt}=\overrightarrow{v};}$$

$$\mathrm{\overrightarrow{v}\times \overrightarrow{p}=m(\overrightarrow{v}\times \overrightarrow{v})=0}$$

（對於任何向量 $\mathrm{\overrightarrow{A}:\overrightarrow{A}\times \overrightarrow{A}=0}$）

因此，我們可以在方程 (1) 的兩邊新增它

$$\mathrm{\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}+\overrightarrow{\tau}=\overrightarrow{r}\times \frac{d\overrightarrow{p}}{dt}+\frac{d\overrightarrow{r}}{dt}\times \overrightarrow{p}=\frac{d(\overrightarrow{r}\times \overrightarrow{p})}{dt}}$$

因此

$$\mathrm{\overrightarrow{\tau}=\frac{d(\overrightarrow{r}\times \overrightarrow{p})}{dt}}$$

如果我們將它與平移運動中的類似力進行比較

$$\mathrm{\sum F=\frac{dp}{dt}}$$

我們可以說項 $\mathrm{(\overrightarrow{r}\times \overrightarrow{p})}$ 是一種動量。

因此，我們定義角動量

$$\mathrm{\overrightarrow{L}=(\overrightarrow{r}\times \overrightarrow{p})}$$

剛體繞定軸的角動量

系統的角動量

設有一個由 n 個粒子組成的系統，它們的各個角動量由 $\mathrm{\overrightarrow{l_1},\overrightarrow{l_2},\overrightarrow{l_3},............\overrightarrow{l_n}}$ 表示，那麼該系統的總角動量可以寫為 -

$$\mathrm{\overrightarrow{L}=\overrightarrow{l_1}+\overrightarrow{l_2}+\overrightarrow{l_3}.................+\overrightarrow{l_n}=\sum_{i}\overrightarrow{L_i}}$$

$$\mathrm{\frac{d}{dt}(\overrightarrow{L})=\sum \frac{d}{dt} \overrightarrow{l_i}=\sum_i \overrightarrow{\tau_{ext,i}}}$$

因此，作用在系統上的總外力矩等於系統總角動量的變化率。

對於剛體

我們將剛體看作是一個由小粒子組成的巨大系統。設每個粒子的質量為 $\mathrm{m_i}$，線速度為 $\mathrm{\overrightarrow{v_i}}$。假設該物體繞 z 軸以角速度 $\mathrm{\overrightarrow{\omega_i}}$ 運動，並且粒子在 x-y 平面上圍繞 z 軸旋轉。

那麼每個粒子的角動量

$$\mathrm{\overrightarrow{L_i}=m_i(\overrightarrow{r_i}\times \overrightarrow{v_i})}$$

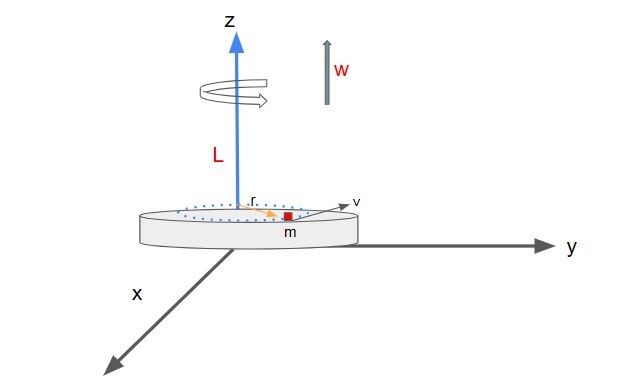
如圖所示，$\mathrm{\overrightarrow{r_i}}$ 和 $\mathrm{\overrightarrow{v_i}}$ 之間的角度為 90°。

$$\mathrm{\Rightarrow\:\:\overrightarrow{L _i}=m_i(\overrightarrow{r_i}\times \overrightarrow{
u_i})= m_i\:r_i\:v_i\: sin90=m_i\:r_i\:v_i}$$

因此

$$\mathrm{\overrightarrow{L _z}=\sum \overrightarrow{L _i}=\sum m_i\:r_i\:v_i}$$

我們知道

$$\mathrm{
u_i=\overrightarrow{r_i\omega}}$$

所以

$$\mathrm{\overrightarrow{L_z}=\omega\sum m_i\:r_i^2=I \overrightarrow{\omega}}$$

since 慣性矩

$$\mathrm{I =\sum m_i\:r_i^2}$$

因此，對於剛體

$$\mathrm{\overrightarrow{L_z}=I \overrightarrow{\omega}}$$

即，剛體繞 z 軸的總角動量等於角動量和慣性矩的乘積。

我們知道 $\mathrm{\overrightarrow{\tau}=\frac{d\overrightarrow{L}}{dt}}$

因此

$$\mathrm{\overrightarrow{\tau}=\frac{d}{dt}(I\overrightarrow{\omega})=I\overrightarrow{\alpha}}$$

即，作用在剛體上的合力矩是其慣性矩和角加速度的乘積。

它為我們提供了力矩和角加速度之間的關係。它類似於牛頓第二定律

平移運動	$\mathrm{\overrightarrow{F}=m\overrightarrow{a}}$	$\mathrm{\overrightarrow{p}=m\overrightarrow{ u}}$
旋轉運動	$\mathrm{\overrightarrow{\tau}=I\overrightarrow{\alpha}}$	$\mathrm{\overrightarrow{L}=I\overrightarrow{\omega}}$

表-2：牛頓第二定律在旋轉和平移運動中

結論

角動量類似於旋轉運動中的線動量。它取決於與旋轉軸的距離。角動量只有在圍繞特定原點定義時才有意義。它是一個向量量，總是垂直於 $\mathrm{\overrightarrow{r}}$ 和 $\mathrm{\overrightarrow{p}}$的平面。角動量變化率給我們粒子上的力矩。我們還可將此概念用於多粒子系統。對於剛體，它等於該物體的角速度乘以慣性矩。我們還可以展示旋轉運動和平移運動之間的對應關係，如表-1 中總結的那樣。

常見問題

Q1. 角動量守恆的條件是什麼？

問題：孤立系統的角動量始終守恆，前提是外部扭矩為零。即 $\mathrm{\overrightarrow{\tau_{ext}}=0}$

問題 2：角動量的物理意義是什麼？

回答：角動量在物理上是物體轉動運動的度量，而扭矩是力轉動效應的度量。

問題 3：圓周運動中粒子的線動量始終在變化，這是否也適用於角動量？

回答：對於圓周路徑上的粒子，$\mathrm{\overrightarrow{L}=(mvr)\hat{k}}$ 因此，如果粒子繞著穿過其中心的軸運動，則角動量不會改變。

問題 4：非旋轉物體是否可以擁有角動量？

回答：是的，假設一個粒子沿著直線上某條路徑運動，如果我們取 O 點為軸，如果 O 點偏離那條直線，那麼我們會得到非零角動量。因為 $\mathrm{\overrightarrow{r}\times \overrightarrow{v}}$ 將非零。

問題 5：一個球體和一個相同質量的圓柱體繞著相同的軸線以相同角速度旋轉，哪個物體將具有更大的角動量？

回答：圓柱體的轉動慣量 > 相同質量的球體的轉動慣量。

因此圓柱體的角動量 > 球體的角動量