角加速度

---

簡介

角加速度是旋轉動力學中的一個概念，就像加速度在直線運動中被定義一樣。從物理上講，它描述了粒子角速度的變化率。由於旋轉運動是圍繞某個軸或點進行的，因此角加速度根據我們原點的選擇具有不同的值。

角加速度可能是由外力矩引起的，也可能是由於物體結構的變化而引起的，而沒有任何外部影響。後一種情況的一個常見例子是，坐在旋轉椅子上的人在將手臂向內拉時獲得角速度。

什麼是角加速度？

角加速度是線性加速度的旋轉對應物。從數學上講，它被定義為角速度對時間的導數，通常用希臘字母 alpha (α) 表示。角加速度是一個向量量，其方向垂直於粒子的運動平面。

角加速度單位

我們知道物體的角位置用弧度來衡量，因此角速度用弧度每秒來衡量。由於角加速度是此量的變化率，因此它的單位可以很容易地推匯出來。

因此，在 SI 系統中，角加速度的單位是弧度每秒平方 (rad/s2)，對應於維度 $\mathrm{T^{−2}}$。

角加速度公式

考慮一個物體，其角位置和角速度分別用 theta $\mathrm{(\theta)}$ 和 omega $\mathrm{(\omega)}$ 表示。角加速度最簡單的公式表示為角速度對時間的導數。

$$\mathrm{\alpha=\frac{d\omega}{dt}}$$

此外，由於角速度本身取決於角位置，我們還有

$$\mathrm{\alpha=\frac{d^2\theta}{dt^2}}$$

角加速度也可以透過將最終和初始角速度之間的差除以相應的時間變化來估計。

$$\mathrm{\alpha=\frac{\omega_2-\omega_1}{t_2-t_1}=\frac{\Delta \omega}{\Delta t}}$$

角加速度示例

1. 一塊石頭被綁在拉緊的繩子上，在 15 秒內達到 30 rad/s 的角速度。求石頭的角加速度。

答案：已知石頭在 15 秒內達到 30 rad/sec 的角速度。

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}=\frac{30-0}{15-0}=\frac{30}{15}=2\:rad/sec^2 }$$

2. 物體的角旋轉由方程 $\mathrm{\theta=3t^4+6t^2-7t+2}$ 給出。求其在 t=7 秒時的角加速度。

答案：使用公式

$$\mathrm{\alpha=\frac{d^2\theta}{dt^2}}$$

$$\mathrm{\alpha=\frac{d^2}{dt^2}(3t^4+6t^2-7t+2)=36t^2+12}$$

在 t=7 秒時

$$\mathrm{\alpha=36×(7)^2+12=1776\:rad/s2}$$

角加速度的應用

加速汽車的車輪

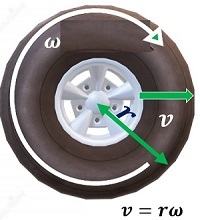
當我們加速或減速汽車時，車輪的角速度相應地增加或減少。也就是說，車輪會受到角加速度，角加速度與汽車的線性加速度透過以下公式關聯

$$\mathrm{\alpha=\frac{a}{r}}$$

吊扇

吊扇起初轉速緩慢，但很快達到所需的轉速。也就是說，它的角速度在達到某個值之前會增加。因此，其運動與角加速度相關。請注意，由於風扇繞其軸旋轉，因此這與前一個示例一樣，是自旋角加速度的一個示例。

角加速度型別

旋轉運動下可能存在兩種型別的運動。

自旋角加速度

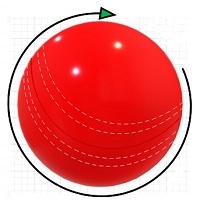
剛體可以繞穿過它的軸旋轉，從而產生粒子的所謂的自旋。一個常見的例子是板球中的旋轉球。

與這種型別的運動相關的角加速度稱為自旋角加速度。

軌道角加速度

另一方面，任何物體，無論是剛性物體還是其他物體，都可以圍繞一個點進行運動，從而產生某種軌道運動。想象這種運動的最簡單方法是觀察行星運動。所有行星都以橢圓軌道繞太陽執行，因此具有軌道運動。這種型別的運動涉及軌道角加速度。

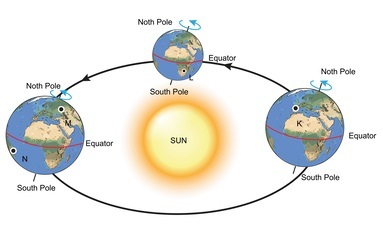
一個物體也可能同時具有自旋和軌道運動。地球的同時自轉和公轉是這種情景的一個非常簡單的例子。

點粒子的軌道角加速度：二維

在二維情況下，當物體相對於一個點運動時，它可能具有角加速度。這被稱為它的軌道角加速度，等於軌道角速度的瞬時變化率。

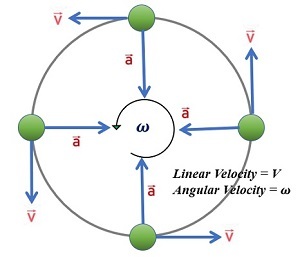
此圖中的綠色箭頭表示粒子瞬時速度的切向分量，而紫色箭頭表示角速度。

$$\mathrm{v=r\omega}$$

$$\mathrm{\omega=\frac{v}{r}}$$

我們知道

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d}{dt}(\frac{v}{r})}$$

要解決此問題，請應用微積分中的乘積法則。我們將得到

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{v}{r^2}(\frac{dr}{dt})}$$

這是點粒子在二維中的軌道角加速度。

特殊情況：如果粒子正在執行圓周運動，這意味著半徑隨時間保持不變。因此，角加速度寫成

$$\mathrm{alpha=\frac{1}{r}\frac{dv}{dt}}$$

角加速度與線性加速度之間的關係

我們再次從推匯出角加速度的公式開始。為此，考慮一個以線性速度 v 運動的物體。然後，角速度為

$$\mathrm{\omega=\frac{v}{r}}$$

因此，

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d}{dt}(\frac{v}{r})}$$

使用乘積法則，

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{v}{r^2}(\frac{dr}{dt})}$$

當粒子的半徑不恆定時，角加速度和線性加速度之間的關係難以制定。

但是，當半徑保持不變時，

$$\mathrm{\frac{dr}{dt}=0}$$

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}}$$

因此，

$$\mathrm{\alpha=\frac{a}{r}}$$

角加速度公式

物體的角加速度可以透過以下任何公式獲得 -

$$\mathrm{\alpha=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}}$$

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}-\frac{v}{r^2}\frac{dr}{dt}}$$

當運動是圓周運動時，

$$\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{a}{r}}$$

解答題

Q1. 物體的角速度在 0.75 秒內從 $\mathrm{\frac{\pi}{4}}$ rad/s 變為 $\mathrm{\frac{3\pi}{8}}$ rad/s。求其角加速度。

答。使用

$$\mathrm{\alpha=\frac{\Delta\omega}{\Delta t}}$$

我們有

$$\mathrm{\alpha=\frac{\frac{3\pi}{8}-\frac{\pi}{4}}{0.75}=\frac{\frac{\pi}{8}}{0.75}=\frac{\pi}{6}\:rad/s^2}$$

Q2. 粒子的角加速度為 3 rad/s²。如果它從靜止開始，求其經過 46 弧度距離後的角速度。

答。設 $\mathrm{\omega_1}$ 和 $\mathrm{\omega_2}$ 為粒子的初始和最終角速度，θ 為所經過的距離。

運動方程為 $\mathrm{\omega_2^{2}-\omega_2^{1}=2\alpha \theta}$

這裡，粒子從靜止開始，因此，$\mathrm{\omega_1=0}$。

因此，

$$\mathrm{\omega_2=\sqrt{2\alpha \theta}=\sqrt{2\times 3\times46}=\sqrt{276}=16.61 rad/s.}$$

結論

角加速度是線性加速度的旋轉對應物，由角速度的變化率給出。它的值根據原點的選擇而變化，因此，即使是直線運動的粒子也可能具有角加速度。對於圓周運動，角加速度由 $\mathrm{\alpha=\frac{1}{r}\frac{dv}{dt}=\frac{a}{r}}$ 給出 運動方程對於旋轉情況和線性情況同樣有效。

常見問題

Q1. 直線運動的粒子是否具有角加速度？

答。是的。根據所選原點，粒子的角速度可能不是恆定的，因此可能存在角加速度。

Q2. 運動方程對於旋轉動力學是否有效？

答。是的，略有修改。旋轉情況下的運動方程如下所示。請注意，為了使這些方程成立，角加速度必須是均勻的。

• $\mathrm{\omega_2^{2}-\omega_1^{2}=2\alpha\theta}$

• $\mathrm{\omega_2=\omega_1+\alpha t}$

• $\mathrm{\theta=\omega_1 t+\frac{1}{2} \alpha t^2}$

Q3. 角加速度的方向是什麼？

答。角加速度向量指向垂直於運動平面的方向。如果角速度沿逆時針方向增加，則其符號為正，否則為負。

Q4. 地球是否具有任何角加速度？

答。地球繞其軸的角加速度幾乎為零。有各種因素導致地球角速度發生無限小的變化，但與地球的實際角速度（大約每天 2π 弧度）相比，這些變化太小了。

Q5. 當粒子在三維空間中運動時，軌道角加速度是多少？

答。在三維空間中，角速度表示為

$$\mathrm{\omega=\frac{r×v}{r^2}}$$

對時間求導，我們得到

$$\mathrm{\alpha=\frac{r\times a}{r^2}-\frac{2}{r}\frac{dr}{dt}\omega}$$

Q6. 簡諧振子的角加速度是多少？

答。對於簡諧振子，運動方程為 $\mathrm{\ddot{\theta}=-\frac{g}{R}\:sin\:\theta}$ 。這是簡諧振子在與垂直方向成 θ 角的瞬時所經歷的角加速度的值。