恆定角加速度

---

引言

恆定角加速度是旋轉動力學中的一個重要概念。在描述線性速度變化時，我們使用線性加速度；然而，當處理旋轉體或曲線運動的物體時，我們使用角加速度。角加速度是線性加速度的旋轉對應物，如同角速度是旋轉速率一樣，這並不令人意外。與定義角速度變化率的角加速度相反，線性加速度解釋了線性速度的變化率。

什麼是角加速度？

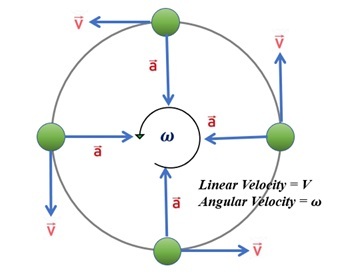
角速度隨時間的變化率稱為角加速度。它是一個三維偽向量。在國際單位制中，我們將其定義為弧度/秒平方(rad/sec²)。此外，我們通常用希臘字母'α’表示它。

有趣的是，角加速度既不是真正的向量，也不是真正的標量。這意味著它像標量一樣運作，因為它只需要一個大小就能完全定義，但根據你觀察的方向，它可能會改變符號。

如何確定角加速度？

藉助角加速度，我們可以修改由時間變化分隔的角速度。利用這一點可以很容易地獲得正常的角加速度。角加速度將其運動方向指向樞軸方向。為了獲得角加速度的程度，我們使用一個方程，

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}=\frac{\omega_2-\omega_1}{t_2-t_1}}$$

旋轉物體的角加速度是指角速度變化相對於所用時間的頻率。它是隔離角速度變化的時間變化。角速度的變化除以時間的變化就是正常的角加速度。

什麼導致角加速度？

加速度與運動有關，無論是角運動還是線性運動。因此，我們知道運動總是由力驅動的。所以，角加速度也有一個力源導致它。

當旋轉一個擴充套件物體（例如其質量分散在空間中的杆、圓盤或立方體）時，我們必須考慮力的位置。

力矩是衡量力啟動旋轉能力的指標。根據物理學原理，作用於物體的力矩取決於所施加力的位置和大小。當我們考慮力矩（導致旋轉加速度）時，你從力的嚴格線性概念（作為沿直線作用的實體）轉移。

力矩是一個向量量。力矩的大小提供了關於其產生旋轉能力的資訊；更準確地說，力矩的大小與它產生的角加速度成反比。力矩沿角加速度的軸施加。

一些與角加速度相關的重要的術語

當我們研究角運動時，角加速度是一個非常重要的術語。這裡還有一些與角加速度相關的術語。

角動量

剛體的動量是透過將其轉動慣量乘以其角速度來計算的。如果沒有外力作用於物體上，它就像線性動量一樣，遵循動量守恆原理的基本規則。它可以從粒子的動量表達式推匯出來。

$$\mathrm{L=I×ω}$$

力矩

使物體繞軸旋轉的力稱為力矩。幾乎就像力在直線力學中加速物體一樣，力矩在角方向上加速物體。

力矩也是一個向量量。作用於軸上的力定義了力矩向量的方向。

$$\mathrm{\tau=F.r}$$

角速度

物體的旋轉速率和方向都由其角速度描述。逆時針方向通常被視為正方向。旋轉速率的矢量表示，或物體相對於另一點旋轉或旋轉的速度，稱為角速度。

$$\mathrm{\omega=\frac{\theta}{t}}$$

角加速度的一些實際應用

物理學中的每一個術語在我們的日常生活中都非常適用。在這裡，我們將學習角動量的應用。

• 子彈射出膛線槍管時，膛線會刻在子彈上，使其旋轉。

• 當四分衛用手指旋轉投球時，足球在空中快速旋轉。緊密的螺旋形是球迷們識別好球的方式。

• 刻在槍管上的膛線形成了圍繞槍口出口孔的吸引人的螺旋圖案。

結論

角加速度是線性加速度的旋轉等效物。與定義角速度變化率的角加速度相反，線性加速度解釋了線性速度的變化率。

根據傳統觀點，正角加速度會使旋轉加速到逆時針方向，而負角加速度會使旋轉加速到順時針方向。角加速度的SI單位是弧度每秒平方。

我們用角速度的變化除以時間的變化來確定物體的角加速度。這得到角加速度或每秒角速度的平均變化。

常見問題

Q1. 角加速度的正負號有何意義？

A1. 角加速度的大小是一個正數。但是，我們觀察到角加速度的大小帶有正負號。這些符號對於角加速度的方向非常重要。當角速度逆時針增加時，角加速度的符號被認為是正的；當它順時針增加時，它被認為是負的。

Q2. 角動量對我們有什麼重要性？

A2. 在角速度的背景下，角加速度是角度變化率；其大小和方向分別提供關於變化率和方向的資訊。

Q3. 我們有一個吊扇，它透過將模式從低速切換到高速來開始加速。風扇葉片的加速度為 1.5 rad/s²，持續 2 秒。如果初始角速度為 4 rad/s，現在計算風扇的最終角速度。

A3. 我們知道角加速度是

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}}$$

現在，我們有

初始速度 = 4 rad/s

角加速度 = 1.5 rad/s²

因此，使用角加速度方程

$$\mathrm{\alpha \Delta t=\Delta \omega}$$

$$\mathrm{\alpha \Delta t=\omega_f-\omega_i}$$

因此，

$$\mathrm{\omega_f=\alpha \Delta t+\omega_i}$$

$$\mathrm{\omega_f=1.5×2+4}$$

$$\mathrm{\omega_f=7\:rad/s^2}$$

Q4. 我們有一個正在旋轉的牛頓盤。然而，它以 50 rad/s 的速度改變了旋轉速度。圓盤的速度變化持續 7 秒。現在，評估牛頓圓盤的角加速度大小。

A4. 根據定義，我們知道角加速度是速度變化與時間的比率。

因此

$$\mathrm{\alpha=\frac{\Delta \omega}{\Delta t}}$$

$$\mathrm{\alpha=\frac{50}{7}}$$

$$\mathrm{\alpha=7.14\: rad/s^2}$$