複數的代數運算

---

介紹

複數的代數運算由算術運算給出，包括加法、減法、乘法和除法。複數使得求負數的平方根更加簡單。複數的概念最早出現在公元一世紀，當時一位希臘數學家亞歷山大城的希羅嘗試計算負數的平方根。

許多科學研究，包括涉及訊號處理、電磁學、流體物理學、量子力學和振動分析的研究，都使用了複數。在本教程中，我們將討論複數的代數運算。

複數

複數是由實數和虛數組合而成的。複數的格式為 a + ib，其中 ib 是虛部，a 是實部。

因此，複數是實數和虛數相加的簡單表示式。a 是純實數，b 是純虛數。

實數 − 所有存在於數系表示法中的數，例如正數、負數、零、整數、有理數、無理數和分數，都是實數。

虛數：不是實數的數是虛數。虛數的平方等於負數，表示為 i=√(-1)。

複數運算

複數的代數運算在數學中由四個基本的算術運算表示：加法、減法、除法和乘法。複數是實數和虛數的乘積。

加法和減法

• 複數加法

  在複數加法中，實部和虛部分別相加。

  如果，Z₁=m+in 和 Z₂=p+iq，則

  $$\mathrm{Z_1+Z_2=(m+p)+i(n+q)}$$

• 兩個複數的減法

  在兩個複數的減法中，實部和虛部分別相減。

  如果，Z₁=m+in 和 Z₂=p+iq，則

  $$\mathrm{Z_1-Z_2=(m-p)+i(n-q)}$$

乘法

使用分配律來乘以兩個或多個複數。如果我們有兩個複數，z = a + ib 和 w = c + id，則複數 z 和 w 的乘法表示為 z.w = (a + ib) (c + id)。為了求複數的乘積，我們使用乘法的分配律。

$$\mathrm{z.w = (a + ib) (c + id). }$$

$$\mathrm{z.w = (ac-bd)+i(ad+bc) }$$

除法

要除以複數，我們必須找到一個可以同時乘以分子和分母的項，並消除分母的虛部，從而得到分母為實數的結果。

如果 z = a + ib 和 w = c + id

則 $\mathrm{\frac{z}{w}=\frac{a + ib}{c + id}}$

現在乘以併除以 c - id

$$\mathrm{\frac{z}{w}=\frac{a + ib}{c + id}×\frac{c - id}{c - id}}$$

$$\mathrm{\frac{z}{w}=\frac{(ac+bd)}{c^2+d^2}+i \frac{(bc-ad)}{c^2+d^2}}$$

極座標形式

複數的極座標形式以與直角座標形式不同的方式表示複數。複數是實數和虛數的組合。複數的格式為 a + ib。

但是，複數在極座標形式中表示為模和幅角的組合。複數的模也稱為絕對值。這種極座標形式使用座標系的實軸和虛軸（想象的）極座標來表示。

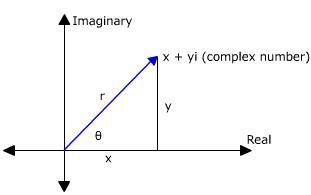
這裡，縱軸表示虛軸（想象的），而橫軸表示實軸。計算 r 以確定座標的實部和虛部。r 是向量的長度，θ 是與實軸形成的角度。

$$\mathrm{z = x + iy.}$$

$$\mathrm{z= r (cosθ + i sinθ)}$$

對於複數，r 表示絕對值或模，角度 θ 稱為複數的幅角 $\mathrm{r=|z|=\sqrt{x^2+y^2}.}$

極座標形式的運算

請按照以下方法在極座標形式下加/減複數：

• 將所有複數從極座標轉換為直角座標表示。

• 對直角座標形式的複數進行加法或減法運算。

• 在計算結果後，將結果轉換回極座標形式。

例題

1) 簡化 (1+i)×(4+3i)

答案：給定方程為 (1+i)×(4+3i)

$$\mathrm{\Rightarrow (4-3)+i(3+4)}$$

$$\mathrm{\Rightarrow 1+7i}$$

2) 簡化 (2+i)×(2+2i)

答案：給定方程為 (2+i)×(2+2i)

$$\mathrm{\Rightarrow (4-2)+i(4+2)}$$

$$\mathrm{\Rightarrow 2+6i}$$

3) 簡化 (11+2i)-(14+3i)

答案：在兩個複數的減法中，實部和虛部分別相減。

$$\mathrm{(11+2i)-(14+3i)}$$

$$\mathrm{\Rightarrow (11-14)+(2i-3i)}$$

$$\mathrm{\Rightarrow -3-i}$$

4) 簡化 (8+5i)+(6+9i)

答案：在複數加法中，實部和虛部分別相加。

$$\mathrm{(8+5i)+(6+9i)}$$

$$\mathrm{ \Rightarrow (8+6)+(5i+9i)}$$

$$\mathrm{ \Rightarrow 14+14i}$$

5) 簡化： (1+2i)×(2+3i)+(3+2i)

答案：給定方程為 (1+2i)×(2+3i)+(3+2i)

$$\mathrm{\Rightarrow (2-6)+i(4+3)+(3+2i)}$$

$$\mathrm{\Rightarrow (-4+7i)+(3+2i)}$$

$$\mathrm{\Rightarrow -1+9i}$$

6) 求複數 z=11+12i 的模

答案：給定複數為 z=1+2i，我們必須求模，即

$$\mathrm{|z|=\sqrt{(1)^2+(2)^2}}$$

$$\mathrm{|z|=\sqrt{5}}$$

7) 簡化複數 $\mathrm{z=\frac{3+4i}{\sqrt{2}+i}}$

答案：給定複數為 $\mathrm{z=\frac{3+4i}{\sqrt{2}+i}}$

現在，在分子和分母中乘以它的共軛複數

$$\mathrm{z=\frac{3+4i}{√2+i}×\frac{√2-i}{√2-i}}$$

$$\mathrm{z=\frac{3√2+4√2 i-3i+4}{2-1}}$$

$$\mathrm{z=(3√2+4)+i(4√2-3)}$$

8) 求複數 z=4+3i 的平方。

答案：給定複數為 z=4+3i。

$$\mathrm{|z|=\sqrt{(4)^2+(3)^2}}$$

$$\mathrm{|z|=\sqrt{25}}$$

$$\mathrm{|z|=5}$$

且 a=4，b=3。

現在使用複數平方根的公式

$$\mathrm{\sqrt{a+ ib}=±(\sqrt{\frac{|z|+a}{2}}±\frac{ib}{|b|} \sqrt{\frac{|z|-a}{2}})}$$

現在代入值

$$\mathrm{\sqrt{a+ ib}=±(\sqrt{\frac{5+4}{2}}±\frac{i3}{|3|} \sqrt{\frac{5-3}{2}})}$$

$$\mathrm{\sqrt{a+ ib}=±(\frac{9}{2}+i)}$$

9) 求解二次方程 x²-x+1=0 的根

答案：我們知道二次方程公式是 $\mathrm{x=\frac{-b±\sqrt{b^2-4ac}}{2a}}$

現在將此公式應用於給定方程：

$$\mathrm{x=\frac{1±\sqrt{1^2-4.1.1}}{2.1}}$$

$$\mathrm{x=\frac{1±\sqrt{-3}}{2}}$$

$$\mathrm{x=\frac{1±i\sqrt{3}}{2}}$$

10) 求解二次方程 x²-3x+3=0 的根

答案：我們知道二次方程公式是 $\mathrm{x=\frac{-b±\sqrt{b^2-4ac}}{2a}}$

現在將此公式應用於給定方程：

$$\mathrm{x=\frac{3±\sqrt{(-3)^2-4.1.3}}{2.1}}$$

$$\mathrm{x=\frac{3±\sqrt{9-12}}{2}}$$

$$\mathrm{x=\frac{3±i\sqrt{3}}{2}}$$

結論

複數是由虛數和實數相加而成的。複數通常具有 a + ib 的形式，並用符號 z 表示。

在這種情況下，因為 a 和 b 都是實數，所以使用 Re(z) 來表示值“a”作為實部，使用 Im(z) 來表示值“b”作為虛部，ib 也被稱為虛數。

常見問題

1.什麼是複數？

複數是由實數和虛數組合而成的。複數的格式為 a + ib，其中 ib 是虛部，a 是實部。

2.在複數中，什麼是虛數單位？

虛數單位用 i 表示，其值為 √(-1) 或 i=√(-1)。

3.什麼是複數的極座標形式？

與直角座標形式不同，複數在極座標形式中以不同的方式表示。複數通常表示為 z = x + iy。

4.什麼是複數的模？

複數 z = a + ib 的模是指該複數在阿甘德平面中到原點的距離。它用符號 | z | 表示，等於 $\mathrm{| z | =\sqrt{(a)^2+(b)^2}}$

5.什麼是尤拉公式？

尤拉公式描述了復指數函式和三角函式之間的關係。

$$\mathrm{z=r( cos x + i sin x)}$$

$$\mathrm{z=r e^{ix}}$$