複數的極座標形式

---

簡介

複數 $\mathrm{z\:=\:x\:+\:iy}$ 的極座標形式為 $\mathrm{r(\cos\theta\:+\:i\:\sin\theta)}$。在數學中，有各種座標系來表示實數。然而，複數系統可以透過兩種方式表示，即直角座標系和極座標系。在本教程中，我們將學習複數、其極座標表示以及一些與複數相關的基本公式，並輔以解題示例。

複數

複數是與虛數相關的數系的一種。換句話說，複數是實數和虛數的總和。虛數不過是負整數的平方根。複數通常表示為 $\mathrm{p\:+\:iq}$ 的形式。在這種情況下，p 是實部，q 是虛部。此外，i 是一個虛數，其值為 $\mathrm{\sqrt{-1}}$。一些複數的例子包括 5 + 6𝑖、−3𝑖、−1 + 9𝑖 等。

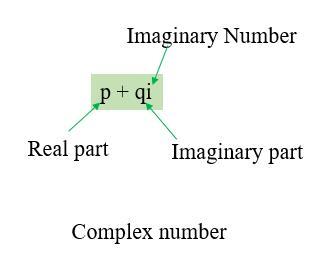
複數的極座標形式

在極座標形式中，複數可以用模和輻角的組合來表示。讓我們考慮一個複數，即 $\mathrm{z\:=\:p\:+\:iq}$。給定複數的極座標形式可以寫成

$$\mathrm{z\:=\:r\:(\cos\theta\:+\:i\sin\theta)}$$

其中 $\mathrm{r\:=\:\lvert\:z\:\rvert\:=\:\sqrt{p^{2}\:+\:q^{2}}\:=\:複數的模}$

$\mathrm{p\:=\:r\cos\theta\:,\:q\:=\:r\sin\theta}$

因此，$\mathrm{\theta\:=\:\tan^{-1}(\frac{q}{p})\:=\:複數的輻角}$

極座標圖的表示

讓我們考慮一個複數，即 $\mathrm{z\:=\:p\:+\:iq}$。複數在極座標形式中的圖形表示如圖所示。

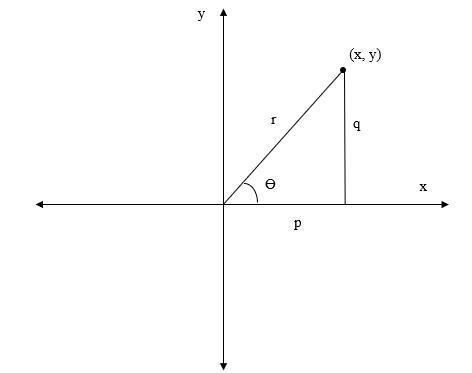
我們可以看到，X 軸表示實部，Y 軸表示複數的虛部。此外，r 是向量的長度，𝜃 是向量與 X 軸所成的角。

現在，使用勾股定理，

$$\mathrm{斜邊^{2}\:=\:底邊^{2}\:+\:高^{2}}$$

$$\mathrm{r^{2}\:=\:P^{2}\:+\:q^{2}}$$

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{p^{2}\:+\:q^{2}}}$$

同樣，$\mathrm{\cos\theta\:=\:\frac{底邊}{斜邊}\:=\:\frac{p}{r}}$（∵使用三角函式）

$$\mathrm{\Longrightarrow\:p\:=\:r\cos\theta}$$

類似地，$\mathrm{\sin\theta\:=\:\frac{高}{斜邊}\:=\:\frac{q}{r}}$（∵使用三角函式）

$$\mathrm{\Longrightarrow\:q\:=\:r\sin\theta}$$

現在，將 p 和 q 的值代入複數的原始方程。我們得到

$$\mathrm{z\:=\:p\:+\:iq\:=\:r(\cos\theta\:+\:i\sin\theta)}$$

得到的表示式是複數的所需極座標形式。

尤拉公式和棣莫弗定理

尤拉公式建立了復指數與三角函式之間的關係。棣莫弗定理用於將複數提升到不同的冪。讓我們詳細討論這兩個公式和定理。

尤拉公式

複數的尤拉公式為 $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

讓我們推匯出這個公式。

尤拉公式的推導 -

$\mathrm{e^{x}}$ 的泰勒級數展開式為

$$\mathrm{e^{x}\:=\:1\:+\:x\:+\:\frac{x^{2}}{2!}\:+\:\frac{x^{3}}{3!}\:+\:\frac{x^{4}}{4!}\:+\:.........}$$

$\mathrm{現在，令\:x\:=\:i\theta}$

因此，$\mathrm{e^{i\theta}\:=\:1\:+\:i\theta\:+\:\frac{(i\theta)^{2}}{2!}\:+\:\frac{(i\theta)^{3}}{3!}\:+\:\frac{(i\theta)^{4}}{4!}\:+\:.........}$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:1\:+\:i\theta\:-\:\frac{\theta^{2}}{2!}\:-\:\frac{i\theta^{3}}{3!}\:+\:\frac{\theta^{4}}{4!}\:+\:.........}$$

$$\mathrm{\Longrightarrow\:e^{i\theta}\:=\:(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:+\:i\:(\theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)}$$

從泰勒級數展開式，

$\mathrm{(1\:-\:\frac{\theta^{2}}{2!}\:+\:\frac{\theta^{4}}{4!}\:+\:.......)\:=\:\cos\theta\:和\:( \theta\:-\:\frac{\theta^{3}}{3!}\:+\:\frac{\theta^{5}}{5!}\:-\:.......)\:=\:\sin\theta}$

因此，$\mathrm{e^{i\theta}\:=\:\cos\theta\:+\:i\:\sin\theta}$ 或 $\mathrm{e^{ix}\:=\:\cos\:x\:+\:i\sin\:x}$

棣莫弗定理

與棣莫弗定理相關的公式為

$$\mathrm{(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$$

棣莫弗公式的推導 -

我們將使用數學歸納法的原理來證明上述公式。

令 $\mathrm{Z(m)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{m}\:=\:p^{m}(\cos\:m\theta\:+\:i\:\sin\:m\theta)}$

情況 1 -

考慮 m = 1

$\mathrm{LHS\:=\:(p(\cos\theta\:+\:i\cos\theta))^{m}\:=\:(p(\cos\theta\:+\:i\:\sin\theta))^{1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

$\mathrm{RHS\:=\:p^{m}\:(\cos\:m\theta\:+\:i\sin\:m\theta)\:=\:p^{1}\:(\cos\:1.\theta\:+\:i\:\sin\:1.\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:=\:p(\cos\theta\:+\:i\:\sin\theta)}$

由於 LHS = RHS，因此 Z (m) 對 m = 1 成立。

情況 2 -

假設上述公式對 m = n 成立

因此，

$\mathrm{Z(n)\:\colon\:(p(\cos\theta\:+\:i\:\sin\theta))^{n}\:=\:p^{n}(\cos\:n\theta\:+\:i\:\sin\:n\theta)}$

情況 3 -

考慮 $\mathrm{m\:=\:n\:+\:1}$

$\mathrm{LHS\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{m}\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n\:+\:1}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))^{n}\:\times\:(p(\cos\:\theta\:+\:i\:\sin\:\theta))}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=\:p^{n}(\cos\:n\:\theta\:+\:𝑖i\:\sin\:n\theta)\:\times\:p(\cos\:\theta\:+\:i\:\sin\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}(\cos\:n\theta\:.\:\cos\theta\:+\:\cos\:n\theta\:.\:i\:\sin\theta\:+\:i\:\sin\:n\theta\:.\:\cos\:\theta\:+\:\sin\:n\theta\:.\:i\sin\:\theta)}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:n\theta\:.\:\cos\:\theta\:-\:\sin\:n\theta\:.\:\sin\theta)\:+\:i(\cos\:n\theta\:.\:\sin\:\theta\:+\:\sin\:n\theta\:.\:\cos\:\theta)]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos\:(n\theta\:+\:\theta))\:+\:i(\sin\:(n\theta\:+\:\theta))]}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:=p^{n\:+\:1}[(\cos(n\:+\:1)\theta)\:+\:i(\sin(n\:+\:1)\theta)]\:=\:RHS}$

由於 LHS = RHS，因此 Z (m) 對 m = n+1 成立。

因此，上述陳述對於 m 的所有值都成立。

解題示例

1)求給定複數 $\mathrm{2\:+\:2i}$ 的輻角和模。

答案 - 給定的複數為

$$\mathrm{z\:=\:2\:+\:2i}$$

複數的輻角由下式給出

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{2}{2}\:=\:\tan^{-1}\:=\:\frac{\pi}{4}}$$

複數的模由下式給出

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{2^{2}\:+\:2^{2}}\:=\:\sqrt{8}\:=\:2\sqrt{2}}$$

∴ 複數的輻角和模分別為 $\mathrm{\frac{\pi}{4}\:和\:2\sqrt{2}}$

2) 使用尤拉公式將 $\mathrm{7e^{3i}}$ 表示為複數的直角座標形式 (p + iq)。

答案 - 使用尤拉公式，

$$\mathrm{e^{i\theta}\:=\:\cos\:\theta\:+\:i\sin\:\theta}$$

這裡，$\mathrm{\theta\:=\:3}$

因此，$\mathrm{e^{3i}\:=\:\cos\:3\:+\:i\sin\:3\:=\:-0.99\:+\:i(0.14)}$

$$\mathrm{7e^{3i}\:=\:7(-0.99\:+\:i(0.14))\:=\:-6.93\:+\:0.98i}$$

因此，$\mathrm{7\:e^{3i}\:=\:-6.93\:+\:0.98i}$

3) 使用棣莫弗公式確定給定複數的值：$\mathrm{(\sqrt{3}\:+\:i)^{6}}$

答案 - 給定的複數為 $\mathrm{\sqrt{3}\:+\:i}$

我們必須將給定的複數轉換為其極座標形式。

複數的輻角由下式給出

$$\mathrm{\theta\:=\:\tan^{-1}\:\frac{1}{\sqrt{3}}\:=\:\frac{\pi}{6}}$$

複數的模由下式給出

$$\mathrm{\Longrightarrow\:r\:=\:\sqrt{(\sqrt{3})^{2}\:+\:1^{2}}\:=\:\sqrt{4}\:=\:2}$$

複數的極座標形式為 $\mathrm{\sqrt{3}\:+\:i\:=\:2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})}$

現在，$\mathrm{(\sqrt{3}\:+\:i)^{6}\:=\:[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}}$

使用棣莫弗公式，

$$\mathrm{[2(\cos\:\frac{\pi}{6}\:+\:i\:\sin\:\frac{\pi}{6})]^{6}\:=\:2^{6}\:(\cos\:\frac{\pi}{6}\:\times\:6\:+\:i\:\sin\:\frac{\pi}{6}\times\:6)}$$

$$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2^{6}\:(\cos\:\pi\:+\:i\sin\:\pi)\:=\:64\:(-1\:+\:i\:.\:0)\:=\:-64}$$

因此，$\mathrm{(\sqrt{3}\:+\:i)^{6}\:的值為-64}$

結論

本教程簡要介紹了複數及其極座標表示。本教程解釋了複數的基本定義及其極座標表示。此外，還說明了與複數相關的兩個重要公式，例如尤拉公式和棣莫弗公式。此外，還提供了一些解題示例，以更好地闡明這一概念。總之，本教程可能有助於理解複數極座標形式的基本概念。

常見問題

1. 尤拉公式有哪些應用？

尤拉公式被廣泛用於確定多面體的邊和頂點之間的關係以及追蹤單位圓。

2. 我們可以將棣莫弗定理應用於以直角座標形式表示的複數嗎？

是的。但是，複數應首先轉換為其極座標形式。然後，我們可以使用棣莫弗公式確定其值。

3. 複數主輻角的範圍是多少？

主輻角的範圍在 $\mathrm{-\pi\:到\:\pi}$ 之間。這意味著 $\mathrm{-\pi\:<\:\theta\:\leq\:\pi}$

4. 複數有哪些應用？

複數廣泛應用於電路分析、訊號處理、量子力學等領域。

5. 複數的模可以為負數嗎？

不可以。複數的模是向量的模長。因此，模長始終為正整數。