複數的輻角
簡介
複數的輻角可以描述為複數所形成的直線與阿根圖平面的正x軸所成的角。複數的輻角描述了複數的虛部和實部之間的關係。在本教程中,我們將瞭解複數、複數的極座標形式、複數的輻角以及一些基於複數的示例。
複數
複數是數系中的元素,由實數和虛數單位 i 組成,其中 i 滿足條件:i2=-1。當複數在阿根圖平面上繪製時,複數的實部和虛部分別標記在 x 軸和 y 軸上。阿根圖平面上的點 X(a, b) 可以表示直線 Z = a + ib,並且直線 OX 與正 x 軸成一定角度。下圖顯示了給定的複數 Z = a + ib 在複平面上表示。此平面用於表示複數的幾何形式。該平面與笛卡爾平面相似,其中 X 軸表示實部,Y 軸表示虛部。
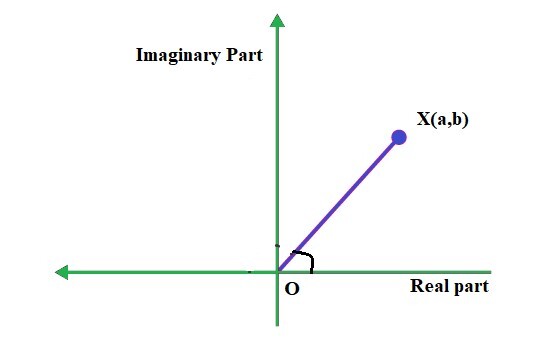
對於複數 Z = a + ib,複數的輻角是角度的度量,它等於複數虛部除以實部所得結果的反三角正切函式。
$$\mathrm{複數的輻角 = θ = Tan^{-1} (b/a)}$$
極座標形式
複數的極座標形式可以表示為 A = r(Cosα + i Sinα)。其中角度 α 和 r 分別為複數的輻角和複數的模。它是表示複數極座標形式的關鍵方法之一。複數極座標形式的座標可以表示為 (rCosα, rSinα)。
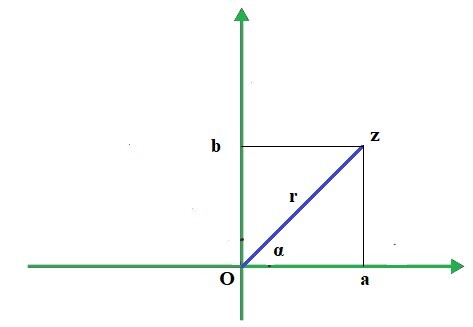
上圖顯示了在阿根圖平面上表示的具有座標 (a,b) 的複數“z”。角度 α 是該直線與正 x 軸所成的角。
複數的輻角
阿根圖平面上的複數可以透過其兩個重要特徵來定義:複數的輻角和模。可以透過計算複數的模來計算複數座標到原點的距離。而複數所形成的直線與正 x 軸所成的角則構成複數的輻角。
arg Z 表示複數 Z =x + iy 的輻角。對於由座標 Z(x, y) 表示的複數 Z = x + iy,以及由 O(0, 0) 表示的直線的原點,直線 OZ 逆時針與正 x 軸所成的角稱為複數的輻角。這樣由複數 Z = x + iy 形成的角度是虛部與實部形成的分數的反正切函式。
$$\mathrm{複數的輻角 =α = Tan^{-1} (y/x)}$$
例題
1)求下列複數的極座標形式。
3 + 3√3i
1+2i.
9+9i
答案
a) 令 Z=3 + 3√3i。
根據公式,我們知道方程的實部 x = 3,虛部 y = 3√3
我們知道,複數的輻角可以透過以下公式計算
$$\mathrm{arg (z) = tan^{-1} (y/x)}$$
$$\mathrm{arg (z) = tan^{-1} (3\sqrt{3}/3)}$$
$$\mathrm{arg (z) = tan^{-1} (\sqrt{3})}$$
$$\mathrm{arg (z) = (π/3)}$$
因此,複數的輻角為 π/3 弧度。
b) 令 Z=√3+i
根據公式,我們知道方程的實部 x = √3,虛部 y =1
我們知道,複數的輻角可以透過以下公式計算
$$\mathrm{arg (z) = tan^{-1} (y/x)}$$
$$\mathrm{arg (z) = tan^{-1} (1/\sqrt{3})}$$
$$\mathrm{arg (z) = (π/6)}$$
因此,複數的輻角為 π/6 弧度。
c) 9+9i
根據公式,我們知道方程的實部 x = 9,虛部 y =9
我們知道,複數的輻角可以透過以下公式計算
$$\mathrm{arg (z) = tan^{-1} (y/x)}$$
$$\mathrm{arg (z) = tan^{-1} (9/9)}$$
$$\mathrm{arg (z) = tan^{-1} (1)}$$
$$\mathrm{arg (z) = (π/4)}$$
因此,複數的輻角為 π/4 弧度。
2) 求下列複數的模和輻角。
3-4i
-5i
-4
解答
我們知道複數的極座標形式可以表示為
$$\mathrm{A = r(Cosα + iSinα)}$$
其中 r=|Z| 和 α=arg(Z)
a)
$$\mathrm{|Z|=\sqrt{3^2+(-4)^2}}$$
$$\mathrm{|Z|=\sqrt{25}}$$
$$\mathrm{|Z|=5}$$
我們知道 r=|Z|=5
$$\mathrm{α=arg(Z)}$$
$$\mathrm{arg (z) =tan^{-1} (-4/3)}$$
因此,複數的極座標形式可以寫成:
$$\mathrm{A=5 Cos (Tan^{-1} (-4/3))+i Sin(Tan^{-1} (-4/3))}$$
b) $\mathrm{|Z|=\sqrt{0^2+(-5)^2}}$
$$\mathrm{|Z|=\sqrt{25}}$$
$$\mathrm{|Z|=5}$$
我們知道 r=|Z|=5
$$\mathrm{α=arg(Z)}$$
$$\mathrm{arg (z) = tan^{-1} (-5/0)}$$
$$\mathrm{arg (z) = -tan^{-1} \frac{π}{2}}$$
$$\mathrm{arg (z) = -\frac{π}{2}}$$
因此,複數的極座標形式可以寫成:
$$\mathrm{A=5 Cos (-\frac{π}{2})+i Sin(-\frac{π}{2})}$$
c) $\mathrm{ |Z|=\sqrt{4^2+(0)^2}}$
$$\mathrm{|Z|=\sqrt{16}}$$
$$\mathrm{|Z|=4}$$
我們知道 r=|Z|=4
$$\mathrm{α=arg(Z)}$$
$$\mathrm{arg (z) = tan^{-1} (0/4)}$$
$$\mathrm{arg (z) = tan^{-1} π}$$
$$\mathrm{arg (z) =π}$$
因此,複數的極座標形式可以寫成:
$$\mathrm{A=4 Cos (π)+i Sin(π)}$$
結論
複數的輻角可以描述為複數所形成的直線與阿根圖平面的正x軸所成的角。複數是數系中的元素,由實數和虛數單位 i 組成,其中 i 滿足條件:i2=-1。複數的極座標形式可以表示為 A = r(Cosα + i Sinα)。可以透過計算複數的模來計算複數座標到原點的距離。
| 表示式 | 含義 |
|---|---|
| Z=a+ib | (a,b) 表示阿根圖平面上的座標。 |
| A = r(Cosα + i Sinα) | 表示複數的極座標形式。 |
| r=|Z| | 表示複數的模。 |
| α=arg(Z) | 表示複數的輻角。 |
常見問題
1. 複數輻角的常用範圍是多少?
複數輻角的常用範圍是 (-π,π)
2. 對於兩個複數,arg(Z1/Z2) 的值是多少?
根據複數輻角的性質,arg(Z1/Z2)=arg(Z1)-arg(Z2)
3. 對於兩個複數,arg(Z1×Z2) 的值是多少?
根據複數輻角的性質,arg(Z1×Z2)=arg(Z1)+arg(Z2)
4. 在複數形式 Z=a+ib 中,“i” 是什麼?
“i” 稱為虛數單位。虛數單位表示 -1 的平方根,即 √(-1)
5. 什麼是阿根圖?
阿根圖用於表示複數,其中橫軸表示實部,縱軸表示虛部。


 資料結構
資料結構 網路
網路 關係型資料庫管理系統
關係型資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP