資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學正則表示式如何轉換為有限自動機（NFA）？
正則表示式是標記的表示。但是，要識別標記，可能需要標記識別器，它就是一個有限自動機（NFA）。因此，可以將正則表示式轉換為NFA。
正則表示式轉換為NFA的演算法
輸入 − 正則表示式 R
輸出 − 接受由 R 表示的語言的 NFA
方法
對於 ε，NFA 是
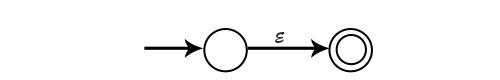
對於 a，NFA 是
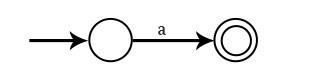
對於 a + b，或 a | b，NFA 是
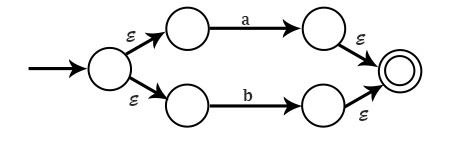
對於 ab，NFA 是
對於 a*，NFA 是
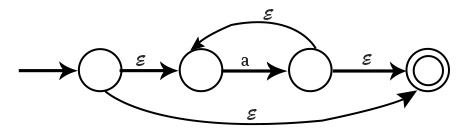
示例 1 − 為正則表示式 a(a+b)*ab 繪製 NFA
解答
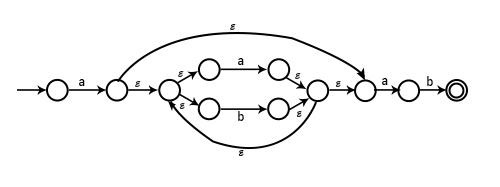
示例 2 − 為 a + b + ab 繪製 NFA
解答
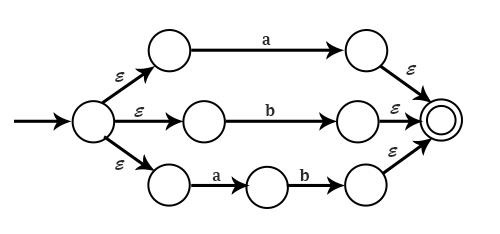
示例 3 − 為 letter (letter+digit)* 繪製 NFA
解答
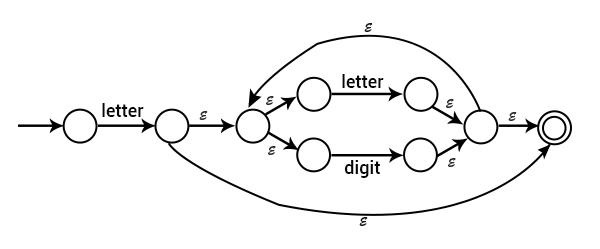
示例 4 − 為 (0+1)*1(0+1) 繪製對應的 NFA
解答
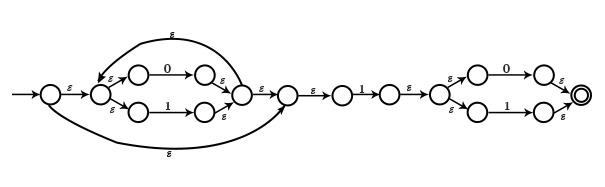
ε−閉包 (s) − 它是由狀態 s 透過僅 ε-轉移所能到達的狀態集。
- 如果 s、t、u 是狀態。初始時，ε−閉包 (s) = {s}。
- 如果 s→t，則 ε−閉包 (s) = {s, t}。
- 如果 s→t→u，則 ε−閉包 (s) = {s, t, u}
將重複此過程，直到覆蓋所有狀態。
演算法：ε−閉包 (T)
T 是一組狀態，需要找到其 ε−閉包 (s)。
壓入 將 T 中的所有狀態壓入堆疊
ε −閉包 (T) = T
While (stack not empty) {
Pop s, the top element of Stack
for each state t, with edge s→t {
if t is not present in ε−closure (T) {
ε−closure (T)=ε−closure (T)∪{t}
Push t on Stack
}
}
}示例 − 為以下 NFA 查詢 ε−閉包(0)、ε−閉包(1)、ε−閉包(4)。
解答
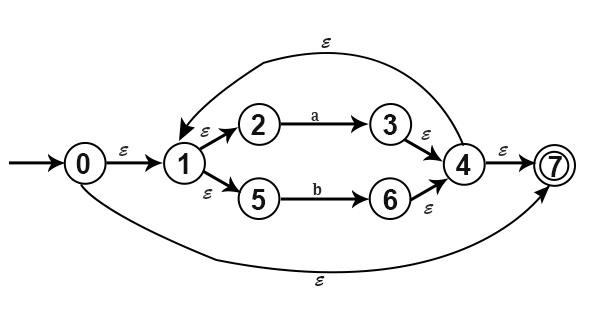
ε−closure(0)={0,1,2,5,7}
ε−closure(1)={1,2,5}
ε−closure(4)={4,7,1,2,5}
更新於：2021年10月26日
26K+ 次瀏覽
廣告