從給定的正則表示式設計有限自動機。

有限自動機 (FA) 是一種抽象的計算裝置。它可以用以下方式表示：

  • 圖形化（狀態轉換圖）
  • 表格化（狀態轉換表）
  • 數學化（狀態轉換函式）

FA 的正式定義是它是五元組。

M=(Q, Σ, δ, q0, F)

其中，

  • Q：稱為狀態的有限集合
  • Σ：稱為字元集的有限集合
  • δ：Q × Σ → Q 是狀態轉換函式
  • q0 ∈ Q 是起始或初始狀態
  • F：結束或接受狀態

正則表示式

正則表示式可用於描述定義字串的一系列模式。它用於匹配字串中的字元組合。

某些正則表示式接受的語言稱為正則語言

現在讓我們考慮 **RE 10+(0+11)0*1**，

為該正則表示式構建有限自動機：

步驟 1

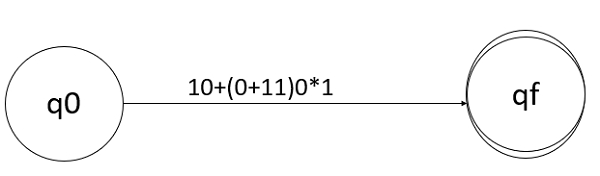
最初考慮兩個狀態 q0 和 qf。此外，考慮初始和最終狀態，q0 到 qf 和給定的正則表示式 10+(0+11)0*1

步驟 2

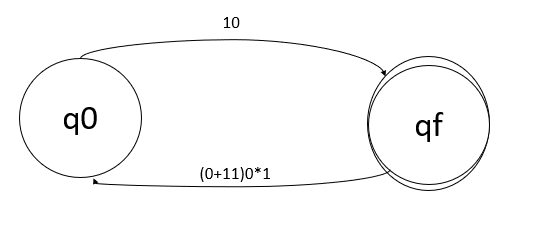
現在應用並集運算，q0 上的 10 轉到 qf，q0 上的 (0+11)0*1 轉到 qf。

步驟 3

現在，透過應用連線來劃分表示式，即設 L1=0，L2=1。連線兩者，我們得到 L= L1.L2。

將此公式應用於正則表示式，因此 q0 上的 1 轉到 q1，q1 上的 0 轉到 qf。類似地，q0 上的 (0+1) 轉到 q2，q2 上的 0*1 轉到 qf。

步驟 4

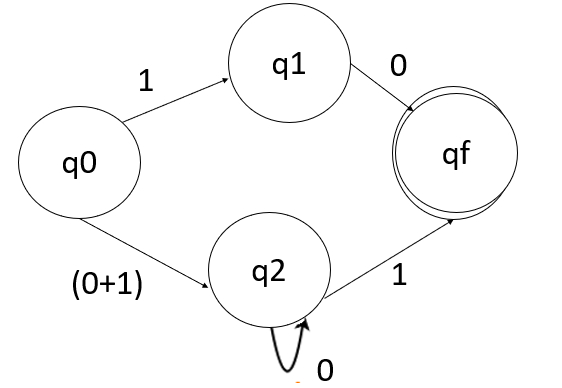
q0 上的 1 轉到 q1，q1 上的 0 轉到 qf，q0 上的 (0+1) 轉到 q2，q2 上的 0 轉到 q2 本身，q2 上的 1 轉到 qf。

步驟 5

給定正則表示式的最終有限自動機如下所示：

更新於： 2021年6月12日

2K+ 次瀏覽

啟動您的 職業生涯

透過完成課程獲得認證

開始學習
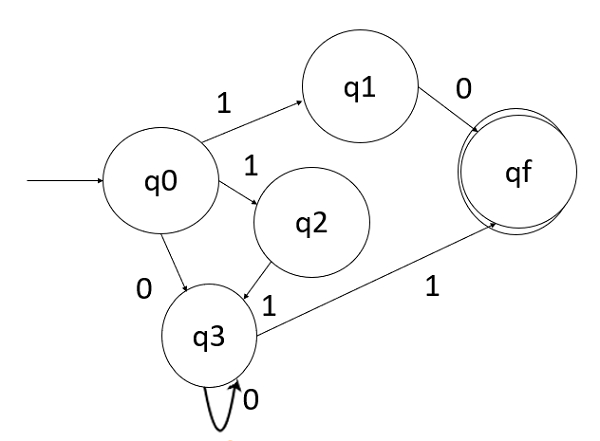
廣告