資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學如何從有限自動機生成正則表示式？
將確定性有限自動機 (DFA) 轉換為正則表示式 (RE) 有兩種方法。它們如下所示：
- Arden 方法
- 狀態消除法
讓我們詳細瞭解這些方法。
Arden 定理
設 P 和 Q 為兩個正則表示式。
如果 P 不包含空字串，則關於 R 的方程 R = Q + RP
其唯一解為 R = QP*
這裡：
有限自動機沒有 ε 移動
它必須只有一個初始狀態 q1
其狀態為 q1, q2, q3,……qn。最終狀態可以是某個 qi，其中 i<=n
qi 是表示有限自動機接受的字串集的正則表示式，即使 qi 是最終狀態。
使用 Arden 定理求 DFA 的 RE
為了找到給定自動機的正則表示式，我們首先為所有狀態建立如下所示的方程：
q1=q1α11+q2α21+----------+qnαn1+𝟄 q2=q1α12+q2α22+-----------+qnαn2 - - - - qn=q1α1n+q2α2n+------------+qnαnn.
透過重複應用替換和 Arden 定理，我們可以用 αij 來表示 qi。為了獲得 FSA 識別的字串集，我們必須取對應於最終狀態的所有 qi 的並集。
示例
注意 - 對於並行邊，該狀態在表示式中將有多個表示式。
然後，我們求解這些方程以獲得 qi 關於 αij 的方程，該表示式就是所需解，其中 qi 是最終狀態。
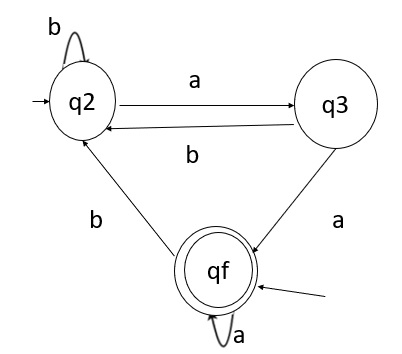
q1 = qa + q3a + ε (ε 移動是因為 q1 是初始狀態)
q2 = q1b + q2b + q3b
q3 = q2a
現在，我們將求解這三個方程
- q2 = q1b + q2b + q3b
q2 = q1b + q2b + (q2a)b (代入 q3 的值)
q2 = q1b + q2(b + ab)
q2 = q1b(b + ab)* (應用 Arden 定理)
- q1 = q1a + q3a + ε
q1 = q1a + q2aa + ε (代入 q3 的值)
q1 = q1a + q1b(b + ab)*aa + ε (代入 q2 的值)
q1 = q1(a + b(b + ab)*aa) + ε
q1 = ε(a + b(b + ab)*aa)*
q1 = (a + b(b + ab)*aa)*
因此，正則表示式為 (a + b(b + ab)*aa)*。
狀態消除法
步驟 1
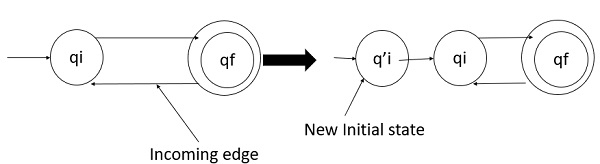
DFA 的初始狀態沒有任何入邊。
如果初始狀態存在任何入邊，則需要建立一個沒有入邊的新的初始狀態。
示例
步驟 2
DFA 中必須只有一個最終狀態。
如果 DFA 中存在多個最終狀態，則需要將所有最終狀態轉換為非最終狀態，並建立一個新的單個最終狀態。
示例
步驟 3
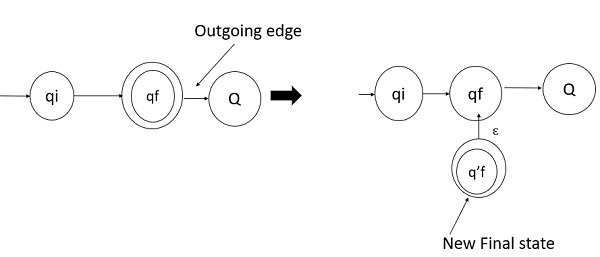
DFA 的最終狀態沒有任何出邊。
如果最終狀態存在任何出邊，則需要建立一個沒有出邊的新的最終狀態。
示例
步驟 4
依次消除所有中間狀態。這些狀態可以按任何順序消除
最後，將只剩下一個初始狀態到最終狀態。
此轉換的成本是所需的正則表示式。
2K+ 次檢視
