在理論計算機科學中解釋確定性有限自動機。
DFA 指的是確定性有限自動機。確定性指的是計算的唯一性。如果機器一次讀取一個輸入符號的輸入字串,則有限自動機是確定性 FA。
在 DFA 中,從當前狀態到下一狀態只有一個路徑輸入。它不接受空移動,即它不能在沒有任何輸入的情況下更改狀態。它可以包含多個最終狀態。它用於編譯器中的詞法分析。
不同自動機(DFA)的形式化定義
確定性有限自動機 (DFA) 是一個集合,定義為 5 元組,如下所示:
M=(Q, Σ, δ,q0,F)
其中,
- Q:稱為狀態的有限集。
- Σ:稱為字母表的有限集。
- δ:Q × Σ → Q 是轉移函式。
- q0 ∈ Q 是起始狀態或初始狀態。
- F:最終狀態或接受狀態。
DFA 的圖形表示
DFA 可以用稱為狀態圖的有向圖表示。
DFA 中考慮以下因素:
- 狀態由頂點表示。
- 用輸入字元標記的弧表示轉換。
- 初始狀態用箭頭表示。
- 最終狀態用雙圓圈表示。
DFA 中的陷阱狀態
如果轉換到一個它永遠無法逃脫的狀態。這種狀態稱為陷阱狀態。它被稱為死狀態。
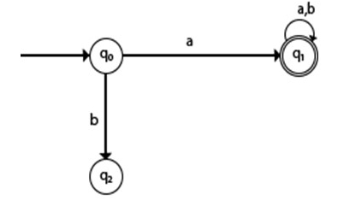
在上面的例子中,q2 是一個陷阱狀態或死狀態,因為它無法到達最終狀態。
DFA(確定性有限自動機)的應用
確定性有限自動機的不同應用如下:
- 協議分析文字解析。
- 電子遊戲角色行為。
- 安全分析。
- CPU 控制單元。
- 自然語言處理語音識別等。
示例
為給定圖構造 DFA 的轉換表。
Q= {q0,q1,q2}
Σ ={0,1}
q0= {q0}
F= {q2}
轉換圖
轉換圖如下所示:
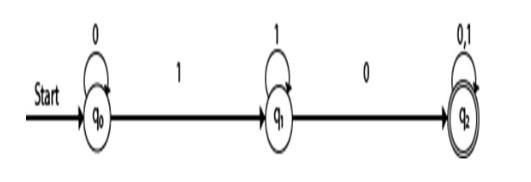
轉換表
轉換表如下所示:
| 當前狀態 | 輸入 0 的下一狀態 | 輸入 1 的下一狀態 |
|---|---|---|
| ->q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
解釋
- 步驟 1 - 在上表中,q0 是初始狀態,輸入“0”時,q0 狀態轉到自身,輸入“1”時,它轉到狀態 q1。
- 步驟 2 - q1 是中間狀態,輸入“0”時,q1 轉到 q2 狀態,輸入“1”時,q1 轉到自身。
- 步驟 3 - q2 是最終狀態,q2 在“0”上轉到 q2 本身,輸入“1”轉到 q2 本身。

廣告

 資料結構
資料結構 網路
網路 關係資料庫管理系統
關係資料庫管理系統 作業系統
作業系統 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 程式設計
C 程式設計 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP