資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究什麼是非確定有限自動機 (NFA)？
非確定性意味著從某個狀態出發，在相同的輸入符號上可能存在多個可能的轉移。對於給定的輸入，輸出是非確定的。NFA 可以表示為非確定有限狀態機。
NFA 可以用 5 元組 (Q,$\sum$,$\delta$,q0,F) 表示。
Q 是一個有限的非空狀態集。
$\sum$ 是一個有限的輸入符號集。
$\delta$ 是從當前狀態轉移到下一個狀態的轉移函式。
∴ $\delta$:Q x $\sum$ → 2Q
q0 ∈ Q 是初始狀態。
F \subseteq Q 是終結狀態集。
示例 1 - 為正則表示式 a(a+b)*ab 繪製 NFA
解決方案
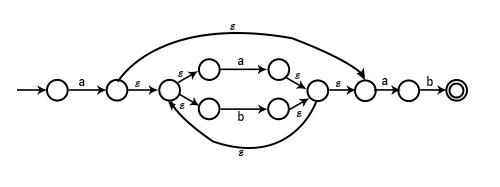
示例 2 - 為 a + b + ab 繪製 NFA
解決方案
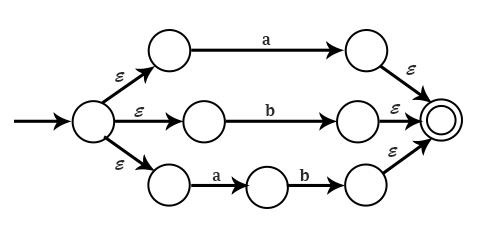
示例 3 - 令 M=(Q,∑,$\delta$,q0,F) 為一個 NFA。證明對於任何 qϵQ 和 a ϵ Σ,$\delta$′(q,a)= $\delta$(q,a)
解決方案
令 M=(Q,∑,$\delta$,q0,F) 為識別語言 L 的 NFA。則滿足以下條件的 DFA，M′=(Q1,∑,$\delta$′,q′0,F′) 識別 L：Q1=2Q，即 Q 的所有子集的集合。
q′0={q0}
$\delta$(q,a)=∪pϵq$\delta$(p,a) 對於 Q1 中的每個狀態 q 和 Σ 中的每個符號 a 以及
F={qϵQ1|q∩F2≠ф}
為了獲得 DFA M′=(Q1,Σ,$\delta$′,q′0,F′)，它接受與給定 NFA，M=(Q,∑,$\delta$,q0,F) 相同的語言。可以按如下步驟進行 -
步驟 1 - 最初 Q1=ф
步驟 2 - 將 {q0} 放入 Q1 中。{q0} 是 DFA M′ 的初始狀態。
步驟 3 - 然後對於 Q1 中的每個狀態 q 執行以下操作：新增此新狀態，將 δ(q,a)=∪pϵqδ(p,a) 新增到 δ 中，其中右側的 δ 是 NFA M′ 的 δ。
步驟 4 - 重複步驟 3 直到有新狀態需要新增到 Q1 中，如果有要新增到 Q1 中的新狀態，則過程終止。
示例 4 - 證明如果 L 被具有 ∈-轉移的 NFA 接受，則 L 被不具有 ∈-轉移的 NFA 接受。
解決方案
假設 L = L (D) 對於某些不具有 ∈-轉移的 DFA 或 NFA。可以透過為 D 的所有狀態 q 新增轉移 δ(q,∈)=ф 來將其轉換為 ∈-DFA (E)。還可以將 D 上輸入符號的轉移例如 δD(q,a)=D 移動到 NFA 轉移到僅包含 P 的集合中，即 δE(q,a)={P}。因此，E 和 D 的轉移是相等的，但 E 明確指出 E 的任何狀態都沒有轉移。
令 E=(QE,Σ,δE,q0,FE) 為 ∈-NFA。可以使用上面表示的修改後的子集構造來建立 DFA。
D=(QE,∑,δE,qD,FD)
L(D)=L(E)，因為 E 和 D 的擴充套件轉移函式是相等的。擴充套件轉移函式是取狀態 q 和字串 w 並返回狀態 P 的函式，即自動機在從狀態 q 開始並處理輸入序列 w 時到達的狀態。
δE(q0,w)=δD(qD,w) 透過對 w 的長度進行歸納。
2K+ 次檢視
