資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究在理論計算機科學（TOC）中解釋非確定性有限自動機。
NFA 代表非確定性有限自動機。與給定正則語言的 DFA 相比，構建 NFA 比較容易。
當存在許多從當前狀態到下一個狀態的特定輸入路徑時，有限自動機被稱為 NFA。
每個 NFA 都可以轉換為 DFA，但每個 NFA 都是非 DFA。
NFA 的定義方式與 DFA 相同，但以下兩個例外情況除外：
- 它包含多個下一個狀態。
- 它包含 ε 轉移。
示例
狀態轉換圖如下所示：
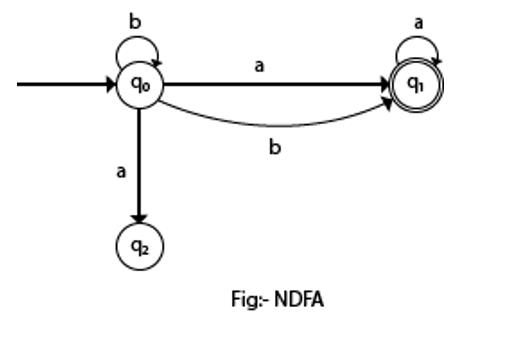
在上面的 NFA 中，很明顯，存在許多從當前狀態到下一個狀態的特定輸入路徑。（狀態 q0 在輸入“b”時，它會進入 q0 本身和 q1）。
非確定性有限自動機也具有與 DFA 相同的五個狀態，但具有不同的轉換函式，如下所示：
δ: Q X Σ -> 2Q
非確定性有限自動機定義為一個 5 元組，
M=(Q, Σ, δ,q0,F)
其中，
- Q：狀態的有限集合
- Σ：輸入符號的有限集合
- q0：初始狀態
- F：最終狀態
- δ：轉移函式：Q X Σ -> 2Q
NFA 的圖形表示
NFA 可以用稱為狀態圖的有向圖來表示。
在圖形化表示 NFA 時，需要考慮以下因素：
- 狀態由頂點表示。
- 用輸入字元標記的弧表示轉換。
- 初始狀態用箭頭標記。
- 最終狀態用雙圓圈表示。
示例 1
Q = {q0, q1, q2}
Σ = {0, 1}
q0 = {q0}
F = {q2}
狀態轉換圖
狀態轉換圖如下所示：
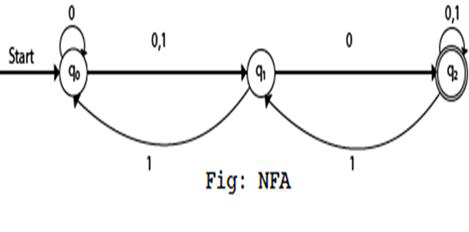
狀態轉換表
狀態轉換表如下所示：
| 當前狀態 | 輸入 0 的下一個狀態 | 輸入 1 的下一個狀態 |
|---|---|---|
| ->q0 | q0,q1 | q1 |
| q1 | q2 | q0 |
| *q2 | q2 | q1,q2 |
解釋
- 步驟 1 - q1 是初始狀態，在輸入“0”時，它會進入多個狀態 q0 和 q1，在輸入“1”時，會進入狀態 q1。
- 步驟 2 - q1 是中間狀態，在輸入“0”時，會進入狀態 q2，這是一個最終狀態，在輸入“1”時，會進入狀態 q0。
- 步驟 3 - q2 是最終狀態，在輸入“0”時，它會進入 q2 本身，在輸入“1”時，它會進入多個狀態 q1 和 q2。
更新時間： 2021年6月11日
19K+ 瀏覽量
廣告