什麼是確定性有限自動機 (DFA)？

確定性意味著對於每個輸入，自動機只有一個狀態可以從其當前狀態轉換。在確定性有限自動機中，磁頭只能沿一個方向移動以掃描輸入磁帶符號。但在雙向有限自動機的情況下，在掃描輸入符號時，磁帶的磁頭可以從其當前位置向右或向左移動。

確定性有限自動機是一組 5 元組，定義為

M=(Q,Σ,δ,q₀,F)，其中：

• Q：有限控制中存在的非空有限狀態集 (q₀,q₁,q₂)。

• Σ：非空有限的輸入符號集。

• δ：這是一個轉移函式，它接受兩個引數，一個狀態和一個輸入符號，它返回一個由∴ δ：Q x Σ →Q 表示的單個狀態。設 q 為狀態，a 為傳遞給轉移函式的輸入符號。δ(q,a)=q。q 是函式的輸出，它可能是相同的狀態或新的狀態。

• q₀ ∈ Q 是初始狀態。

• F⊆ Q 是最終狀態集。

示例 - 最小化以下 DFA

解決方案

• 製作一個狀態轉移表。

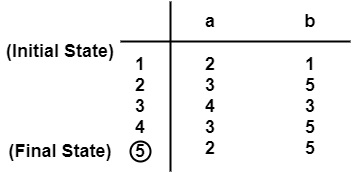
• π₀= {{5}}, {1, 2, 3, 4}}
• 對於輸入 a，在 π₀ 的 {1, 2, 3, 4} 上

• 對於輸入 b，在 π₀ 的 {1, 2, 3, 4} 上

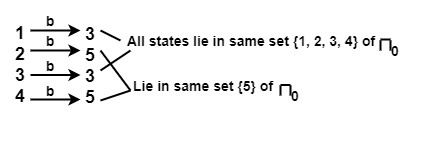
∴ {1, 2, 3, 4} 將被分成 {1, 3} 和 {2, 4}

∴ π₁={{5},{1,3},{2,4}}

• 對於 π₁ 的 {1, 3} 上的輸入符號 a

同樣對於 π₁ 的 {2, 4} 上的輸入符號 a

• 對於 π₁ 的 {1, 3} 上的輸入符號 b

同樣對於 π₁ 的 {2, 4} 上的輸入符號 b

π₁ 中的子集，即 {1, 3} 和 {2, 4} 將不會被分割。

π_final= {{5}, {1, 3}, {2, 4}}

DFA 將有 3 個狀態。

{5}, {1, 3} 和 {2, 4}

最小化的 DFA 將是 -

Ginni

更新於：2021年10月26日

2K+ 次檢視

啟動您的職業生涯

透過完成課程獲得認證

開始