資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟
心理學
社會科學
時尚研究
法律研究理論計算機科學中的線性有界自動機是什麼？
確定性線性有界自動機 (LBA) 是 9 元組自動機
G = ( Q, Σ, E, δ, ε, q0, GL, GR, F)
其中：
Q 是所有狀態的集合
Σ 是所有終結符的集合
E 輸入字母表。
δ 是轉換的集合
q0 初始狀態
GL 磁帶左邊界
GR 磁帶右邊界。
F 終態集合
線性有界自動機是一種具有有限長度的有界磁帶的多軌非確定性圖靈機。
長度 = 函式（初始輸入字串長度，常數 c）
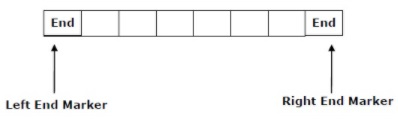
線性有界自動機中的計算限制在常數界定的區域內。此處的輸入字母表包含兩個特殊符號，用作左端標記和右端標記。這說明轉換既不會移動到磁帶的左端標記的左側，也不會移動到磁帶的右端標記的右側。
確定性線性有界自動機是上下文相關的，且空語言的線性有界自動機是不可判定的。
問題
如何構造線性有界自動機來接受語言 L={an|n=m2,m>=1}？
解決方案
對於給定的語言 L={an|n=m2,m>=1}，它生成的字串為 -
L(G) ={a.aa.ab.aaa.aab.abb…….}
S aA, A,aA,A,B,B,bB,B
S aA, aB, a, a (可接受)
S aA, aaA aaB, aa, aa (可接受)
S aA, aB abB, ab, ab (可接受)
SaA, aaA, aaaA, aaa aaa (可接受)
SaA, aaA, aaB, aabB aab, aab (可接受)
SaA, aB, abB, abbB, abb, abb (可接受)
在這裡，我們可以根據產生式集證明 L(G) 中的每個字串都是可接受的語言。
G={{S,AB};{a,b}S, {S aA, A,aA/B, B/bB}}。
更新於： 2021 年 6 月 14 日
9K+ 次觀看
廣告