資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究什麼是理論計算機科學中的 Kleene 定理？
Kleene 定理指出以下三個陳述的等價性：
有限自動機接受的語言也可以被狀態轉換圖接受。
狀態轉換圖接受的語言也可以被正則表示式接受。
正則表示式接受的語言也可以被有限自動機接受。
Kleene 定理證明第一部分
有限自動機接受的語言也可以被狀態轉換圖接受。
考慮一個例子，設 L=aba 在字母表 {a,b} 上。
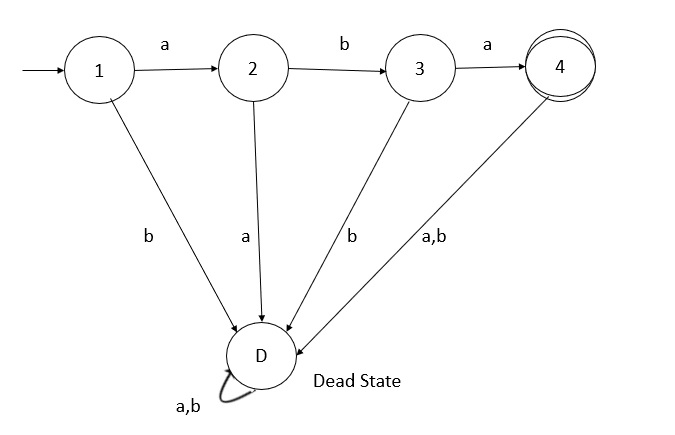
Kleene 定理的第三部分
正則表示式接受的語言也可以被有限自動機接受。
定理
任何可以用正則表示式定義的語言都可以被某個有限狀態機 (FSM) 接受，並且也是正則的。
證明
證明是透過構造來進行的。
對於給定的正則表示式 α，我們可以構造一個 FSM M，使得
L (α) = L (M)
如果 α 是任何 c ∈ Σ，我們可以構造一個簡單的 FSM，如下所示：
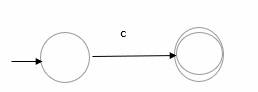
如果 α 是 φ，我們構造一個簡單的 FSM，如下所示：
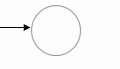
如果 α 是 €，我們構造一個簡單的 FSM，如下所示：
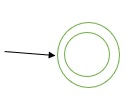
讓我們構造 FSM 來接受由正則表示式定義的語言，這些正則表示式利用連線、並集和 Kleene 星號運算。
步驟 1
設 β 和 γ 是在字母表 Σ 上定義語言的正則表示式。
如果 L(β) 是正則的，則它被某個 FSM 接受。
M1 = (Q1, Σ, δ1, q1, F1)
設 L(γ) 是正則的，則它被某個 FSM 接受。
M2= (Q2, Σ, δ2, q2, F2)
步驟 2
如果正則表示式 α= β ∪ γ，並且 L(β) 和 L(γ) 都是正則的，
那麼我們構造 M3=( Q3, Σ, δ3, q3, F3)，使得
L(M3)=L(α)=L(β) ∪ L(γ)
步驟 3
設 P 接受 L = {a}，Q 接受 L = {b}，則 R 可以表示為 P 和 Q 的組合，使用提供的運算，如下所示：
R = P+ Q
相同的轉換圖如下所示：
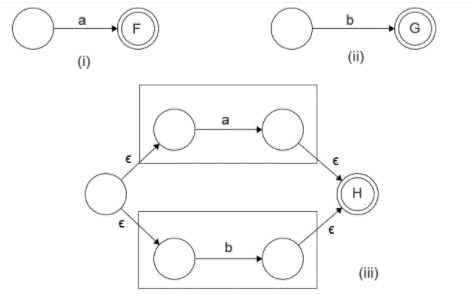
我們在轉換圖中觀察到以下內容：
在並集運算的情況下，我們可以有一個新的起始狀態。從那裡，一個空轉換過程進入兩個有限狀態機的起始狀態。
兩個有限自動機的最終狀態轉換為中間狀態。最終狀態統一為一個，可以透過空轉換遍歷。
17K+ 次瀏覽
