資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學什麼是TOC中的NP完全性？
**非確定性多項式(NP)問題**有點難以理解。就解決NP問題而言，執行時間不是多項式的。它可能是O(n!)或更大的級別。
但是，這類問題給定一個特定的解決方案，檢查該解決方案的執行時間是多項式的。
例如，數獨遊戲。
NP難問題
如果一個用於解決NP難問題的演算法可以轉化為解決任何NP問題，則稱該問題為NP難問題。那麼我們可以說，這個問題至少與任何NP問題一樣難，但它可能更難或更復雜。
NP完全問題
NP完全(NPC)問題是同時存在於NP和NP難類中的問題。也就是說，NP完全問題可以在多項式時間內驗證，並且任何NP問題都可以在多項式時間內簡化為該問題。
如果一個問題在NP類中並且與NP中任何問題一樣難，則該問題屬於NPC類。如果NP中的所有問題都可以在多項式時間內簡化為它，即使它本身可能不在NP類中，則稱該問題為NP難問題。
如果任何這類問題存在多項式時間演算法，則NP中的所有問題都可以用多項式時間求解。這些問題稱為NP完全問題。NP完全性對於理論和實踐都具有重要意義。
NP完全性的定義
如果一個語言M滿足以下兩個條件，則它是NP完全的：
M屬於NP。
NP中的每個A都可以多項式時間歸約到M。
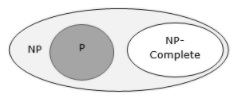
如果一個語言滿足第二個性質，但不一定滿足第一個性質，則該語言M被稱為NP難。
非正式地，如果存在某個NP完全問題A可以圖靈歸約到M，則搜尋問題M是NP難的。
NP完全問題
目前尚不知道存在多項式時間演算法的NP完全問題的例子如下：
確定一個圖是否具有哈密頓迴圈
確定布林公式是否可滿足等。
NP難問題
以下問題是NP難的
電路可滿足性問題
集合覆蓋問題
頂點覆蓋問題
旅行商問題
更新於：2021年6月14日
13K+瀏覽量
廣告