資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究證明頂點覆蓋在理論計算機科學（TOC）中是NP完全的
它是圖G的頂點子集（最小尺寸），使得G中的每條邊都至少與G中一個頂點相關聯。
頂點覆蓋（VC）問題
為了證明VC是NP完全的，我們必須證明以下幾點：
VC是非確定性多項式（NP）的。
一個NPC問題可以歸約到VC。
為了證明VC是NP，找到一個驗證器，它是一個頂點子集，它是VC，並且可以在多項式時間內進行驗證。對於一個有n個頂點的圖，它可以在O(n2)時間內得到證明。因此，VC是NP。
現在考慮“團”問題，它是NPC，並將它歸約到VC以證明NPC。圖G的團是頂點的子集，使得這些頂點在給定的圖G中形成一個完全子圖。
下面給出了VC問題的兩個圖示題（a）和（b）：
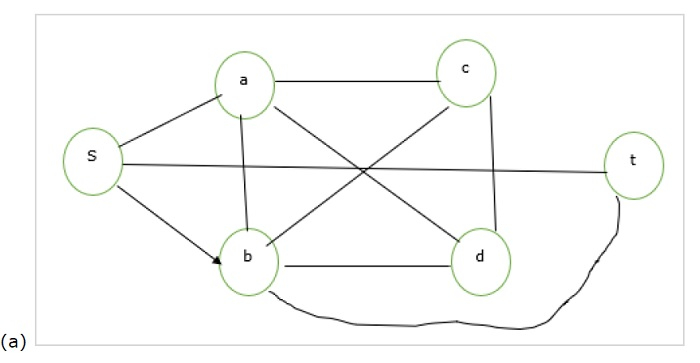
考慮圖（a），這裡團是{a,b,c,d}。
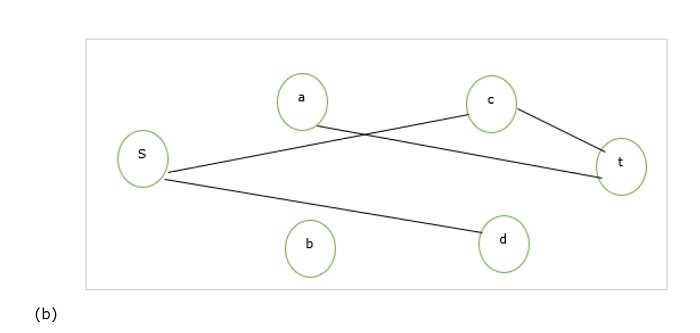
現在計算一個如圖（b）所示的圖，如下所示：
圖（a）中所有頂點的完全圖 - （a）
對於圖（b），我們可以說頂點覆蓋是{s,t}，它覆蓋了（b）的所有邊。這個{s,t} = {a,b,c,d,s,t} – {圖（a）的團} 因此，反過來，我們可以說我們可以將團歸約到VC問題，反過來也可以找到給定無向圖的VC和團。這意味著VC是NP完全可歸約的。
因此證明了VC是NPC。
更新於：2021年6月14日
7K+ 瀏覽量
廣告