資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學圖的支配集是NP完全問題的證明
圖的支配集是NP完全問題，指的是頂點的子集，使得子集中的每個頂點或其相鄰頂點都在子集中。NP的完整形式是“非確定性多項式”，它將在多項式時間內檢查問題，這意味著我們可以在多項式時間內檢查解是否正確。多項式時間對程式碼具有最佳複雜度，例如線性搜尋的時間複雜度為– n, 二分查詢為– logn，歸併排序為– n(log)n等。NP完全圖在合理的時間內提供了一個很好的解決方案。此應用用於網路控制、計算機實驗室拓撲建立、社交網路和分散式計算領域。
讓我們瞭解並檢查節點是否在NP完全問題中具有圖的支配集。
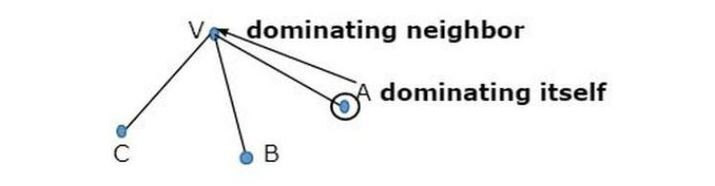
一個頂點被認為支配自身及其每個鄰居。
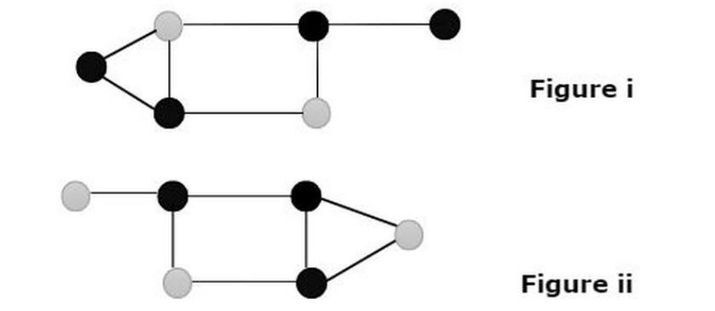
我們看到有兩幅圖顯示圖中灰色節點的支配性質。
G = V, E
引數
G被認為是一個圖，V被認為是一個頂點，E被認為是一條邊。
給定一個圖G(V, E)和一個整數k，確定一個圖是否具有大小為k的支配集。為問題指定的一個輸入被認為是問題的例項。圖G (V, E)和整數k是支配集問題的例子，它詢問圖G中是否可以有一個支配集。由於NP完全問題根據定義既屬於NP又屬於NP-hard，因此證明一個問題是NP完全的問題有兩個組成部分：
支配集在NP完全問題中
如果存在一個NP問題Y可在多項式時間內歸約到X，則X是NP完全的。NP完全問題與NP問題一樣困難。如果一個問題同時屬於NP和NP-Hard問題，則它是NP完全的。在一個非確定性圖靈機中，可以在多項式時間內解決NP完全問題。當一個問題是np完全問題時，它同時具有np和np hard的特性。
這意味著具有np解的問題可以在多項式時間內驗證。
NP完全問題具有支配集的真例項子，例如：
決策問題。
一致的圖。
非確定性搜尋演算法
NP_search( key ) {
arraylist[100];
i = array_check(key);
if(list[i]==key) {
searching found at index i.
} else {
searching found at index i.
}
}
因此，該演算法的總時間複雜度為O(1)，但我們不知道哪種搜尋技術更適合解決這個問題，這被稱為非確定性演算法。
支配集在NP-hard問題中
如果存在一個NP完全問題Y可在多項式時間內歸約到X，則問題X是NP-Hard的。NP-Hard問題與NP完全問題一樣困難。NP-Hard問題不必屬於NP類。
如果每個NP問題都可以在多項式時間內解決，則它被稱為NP-Hard。很多時候，一個特定的問題被用來解決和簡化其他問題。
NP-hard問題具有支配集的真例項子，例如：
哈密頓迴路
最佳化問題
最短路徑
結論
我們學習了圖的支配集是NP完全的概念。我們看到了離散數學是如何作為一個重要方面來連線這些問題的，例如哈密頓迴路、最短路徑等。在程式設計方面，NP完全問題是一類難以找到但易於在多項式時間內驗證解的問題。
396 次瀏覽
