資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究什麼是理論計算機科學中的停機問題？
通常，程式包含長度有限或無限的迴圈。
程式完成的工作完全取決於提供給程式的輸入。
程式可能包含若干不同數量的迴圈，這些迴圈可以是線性或巢狀的。
停機問題是在給定任意計算機程式及其輸入的情況下，確定或推斷該程式是否會停止執行或對於給定輸入執行到無限迴圈的問題。
停機問題表明，編寫一個在有限時間內執行並能夠確定程式是否會為某個輸入停止的計算機程式並不容易。
此外，停機問題從未說過確定給定隨機程式是否會停止是不切實際的。
通常，它會提出類似“給定一個隨機程式和一個輸入，推斷給定隨機程式在給出該輸入時是否會停止”的問題。
編寫停機問題
編寫停機問題的一個例子如下：
輸入 - 程式 P 和字串 S。
輸出 - 如果 P 在 S 上停止，則返回 1。
否則，如果 P 在 S 上進入無限迴圈，則返回 0。
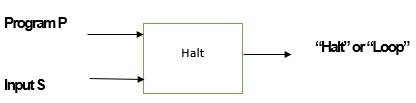
讓我們考慮一個名為 H 的停機問題，它有解決方案。
現在 H 獲取以下兩個輸入：
程式 P
輸入 S。
如果 P 在 S 上停止，則 H 的結果為“停止”，否則 H 的結果為“迴圈”。
H 的圖示表示如下：
示例
ATM = {(M,w) | M 是圖靈機，並且 M 在輸入 w 處停止}。
我們可以構建一個通用圖靈機，它可以在任何輸入上模擬任何圖靈機。
讓我們考慮識別交替圖靈機 (ATM) 的圖靈機：
Recognize-ATM (<M,w>) Simulate M using UTM till it halts If M halts and accept then Accept Else Reject
假設，如果 M 在輸入 w 上進入無限迴圈，則圖靈機 Recognize-ATM 將永遠執行，這意味著圖靈機只是一個識別器，而不是一個判定器。
此問題的判定器將停止對永遠迴圈的模擬。
現在問題是 ATM 是否是圖靈機可判定的，這等同於詢問我們是否可以判斷圖靈機 M 是否會在輸入 w 上停止。
因此，這兩個版本的這個問題通常都被稱為停機問題。
更新於：2021年6月14日
25K+ 瀏覽量
廣告