資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學比較下推自動機和線性有界自動機
讓我們瞭解計算理論 (TOC) 中的下推自動機 (PDA) 和線性有界自動機 (LBA)。
下推自動機
PDA 可以正式描述為七元組 (Q, Σ, S, δ, q0, I, F)
其中：
- Q 是有限數量的狀態
- Σ 是輸入字母表
- S 是棧符號
- Δ 是轉移函式：QX(ΣU{e})XSXQ
- q0 是初始狀態 (q0屬於Q)
- I 是初始棧頂符號
- F 是接受狀態集 (F屬於Q)
下推自動機是一種有限狀態機，它配備了一個作為下推儲存器工作的儲存裝置。
下推自動機等價於上下文無關文法（也稱為喬姆斯基2型文法），這意味著，給定一個上下文無關文法G，可以設計出一個下推自動機A來識別G生成的句子。
這種上下文無關文法和下推自動機之間的關係最早由喬姆斯基（1962年）描述。Yngve（1960年）早些時候使用與下推自動機密切相關的機器來模擬人類處理器分析由上下文無關文法生成的具有各種不同結構的句子所需的瞬時儲存器。
他的方法的基本原理仍然應用於短期記憶和句子處理的研究，其中下推自動機的儲存器用作瞬時儲存器的模型，用於分析具有不同結構的句子。
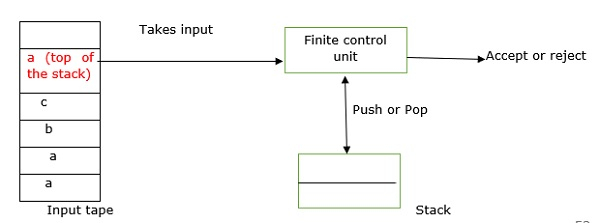
PDA 的組成部分
下推自動機由四個部分組成：
- 控制單元。
- 讀取單元。
- 輸入帶。
- 儲存單元。
控制單元、讀取單元和帶的操作與有限狀態自動機相同，只是下推自動機的控制單元執行的轉換涉及將符號儲存到儲存單元以及從儲存單元檢索符號的操作。
下推自動機的儲存單元作為一個堆疊或下推儲存器工作，這導致了這種抽象機的名稱。
線性有界自動機
線性有界自動機 (LBA) 稱為多軌圖靈機，它只有一個與輸入完全相同長度的磁帶。這似乎相當合理。我們允許計算裝置僅使用在其計算開始時給出的儲存空間。
作為安全措施，我們將在我們的 LBA 磁帶上使用結束標記，並且永遠不允許機器越過它們。這將確保維護儲存邊界，並有助於防止我們的機器離開磁帶。此時，接受集的問題就出現了。讓我們像圖靈機一樣讓線性有界自動機接受。
因此，對於 LBA 來說，停止意味著接受。對於這些新的機器，計算僅限於由常數（軌道數）乘以輸入長度所界定的區域。這非常類似於一個程式設計環境，其中變數的值的大小是有界的。
2K+ 次瀏覽
