資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學凸極同步電機（交流發電機）的雙反應理論
在凸極轉子同步電機中，氣隙高度不均勻。考慮一個具有2極凸極轉子的同步電機，該轉子在2極定子內逆時針旋轉，如圖1所示。
在圖1中，沿轉子軸線所示的軸稱為直軸或d軸，垂直於d軸的軸稱為交軸或q軸。可以看出，d軸磁通($𝜑_{𝑑}$)的路徑涉及兩個較小的氣隙，因此該路徑的磁阻最小。q軸磁通($𝜑_{𝑞}$)路徑具有兩個較大的氣隙，它是磁阻最大的路徑。
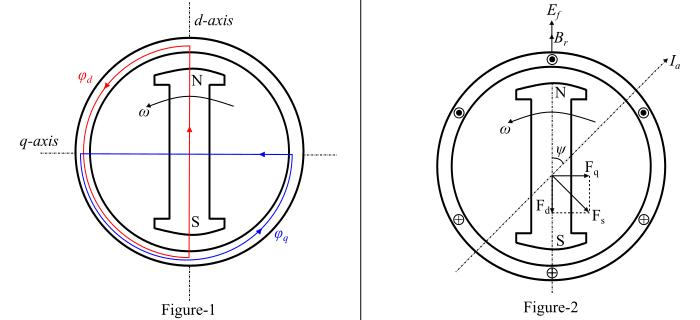
圖2顯示了垂直向上方向的轉子磁場($𝑩_{𝑟}$) 。這個轉子磁場在電樞（或定子繞組）中感應電動勢。
如果將滯後功率因數負載連線到交流發電機，則將流過電樞電流($𝑰_{𝒂}$) 。電樞電流($𝑰_{𝑎}$)滯後於勵磁電壓($𝑬_{𝑓}$) ψ角（見圖2）。電樞電流($𝑰_{𝑎}$)產生定子磁動勢($𝐹_{𝑠}$) ，該磁動勢滯後於$𝑰_{𝒂}$ 90°。定子磁動勢($𝐹_{𝑠}$)沿$𝐹_{𝑠}$方向產生定子磁場($𝑩_{𝒔}$) 。
根據Blondel的雙反應理論，定子磁動勢($𝐹_{𝑠}$)可以分解為兩個分量，即直軸分量($𝐹_{𝑑}$)和交軸分量($𝐹_{𝑞}$) 。
如果
$𝜑_{𝑑}$ = 直軸磁通
$𝜑_{𝑞}$ = 交軸磁通
$𝑆_{𝑑}$ = 直軸磁通路徑的磁阻
$𝑆_{𝑞}$ = 交軸磁通路徑的磁阻
那麼，
$$\mathrm{直軸磁通,\:𝜑_{𝑑} =\frac{𝐹_{𝑑}}{𝑆_{𝑑}}… (1)}$$
並且，
$$\mathrm{交軸磁通,\:𝜑_{𝑞} =\frac{𝐹_{𝑞}}{𝑆_{𝑞}}… (2)}$$
由於$𝑆_{𝑑} < 𝑆_{𝑞}$ ，定子磁動勢的直軸分量($𝐹_{𝑑}$)產生的磁通比定子磁動勢的交軸分量($𝐹_{𝑞}$)產生的磁通多。定子磁通的直軸分量和交軸分量透過電樞反應在定子繞組中產生電壓。
設，
$𝑬_{𝑎𝑑}$ = 電樞反應電壓的直軸分量
$𝑬_{𝑎𝑞}$ = 電樞反應電壓的交軸分量
由於每個電樞反應電壓與其相應的電樞電流成正比，並且滯後於電樞電流90°，因此電樞反應電壓可以寫成：
$$\mathrm{𝑬_{𝑎𝑑} = −𝑗𝑰_{𝑑}𝑋_{𝑎𝑑} … (3)}$$
$$\mathrm{𝑬_{𝑎𝑞} = −𝑗𝑰_{𝑞}𝑋_{𝑎𝑞} … (4)}$$
其中，
$𝑋_{𝑎𝑑}$ 是每相直軸電樞反應電抗。
$𝑋_{𝑎𝑞}$ 是每相交軸電樞反應電抗。
這裡，$𝑋_{𝑎𝑞}$ < $𝑋_{𝑎𝑑}$ ，因為作用在直軸上的給定磁動勢所感應的電動勢由於其較高的磁阻而小於交軸上的電動勢。
現在，電機中感應的合成電動勢為：
$$\mathrm{𝑬_{𝑅} = 𝑬_{𝑓} + 𝑬_{𝑎𝑑 }+ 𝑬_{𝑎𝑞}}$$
$$\mathrm{\Rightarrow\:𝑬_{𝑅}=𝑬_{𝑓}-𝑗𝑰_{𝑑}𝑋_{𝑎𝑑}-𝑗𝑰_{𝑞}𝑋_{𝑎𝑞}… (5)}$$
此外，合成電壓($𝑬_{𝑅}$)等於端電壓與電樞電阻和漏電抗壓降的相量和，因此：
$$\mathrm{𝑬_{𝑅}=𝑽 + 𝑰_{𝑎}𝑅_{𝑎} + 𝑗𝑰_{𝑎}𝑋_{𝑙 }… (6)}$$
電樞電流($𝑰_{𝑎}$)被分成兩個分量，一個與勵磁電壓($𝑬_{𝑓}$)同相，另一個與之正交。
如果
$𝑰_{𝑞}$ = 與$𝑬_{𝑓}$同相的$𝑰_{𝑎}$的交軸分量
$𝑰_{𝑑}$ = 滯後於$𝑬_{𝑓}$ 90°的$𝑰_{𝑎}$的直軸分量
然後，總電樞電流是$𝑰_{𝑞}$和$𝑰_{𝑑}$的相量和，即：
$$\mathrm{𝑰_{𝑎} = Ｉ_{𝑞} + Ｉ_{𝑑} … (7)}$$
現在，根據公式(5)和(6)，我們得到：
$$\mathrm{𝑬_{𝑓} = 𝑽 + 𝑰_{𝑎}𝑅_{𝑎} + 𝑗𝑰_{𝑎}𝑋_{𝑙} + 𝑗𝑰_{𝑑}𝑋_{𝑎𝑑} + 𝑗𝑰_{𝒒}𝑋_{𝑎𝑞} … (8)}$$
並且，根據公式(7)和(8)，我們得到：
$$\mathrm{𝑬_{𝑓} = 𝑽 + (𝑰_{𝑞} + Ｉ_{𝑑})𝑅_{𝑎} + 𝑗(Ｉ_{𝑞} + Ｉ_{𝑑})𝑋_{𝑙} + 𝑗Ｉ_{𝑑}𝑋_{𝑎𝑑} + 𝑗Ｉ_{𝒒}𝑋_{𝑎𝑞}}$$
$$\mathrm{\Rightarrow\:𝑬_{𝑓 }= 𝑽 + (Ｉ_{𝑞 }+ Ｉ_{𝑑})𝑅_{𝑎} + 𝑗Ｉ_{𝑑}(𝑋_{𝑙} + 𝑋_{𝑎𝑑}) + 𝑗Ｉ_{𝑞} (𝑋_{𝑙} + 𝑋_{𝑎𝑞} )}$$
$$\mathrm{\Rightarrow\: 𝑬_{𝑓 }= 𝑽 + (Ｉ_{𝑞} + Ｉ_{𝑑})𝑅_{𝑎} + 𝑗Ｉ_{𝑑}𝑋_{𝑑 }+ 𝑗Ｉ_{𝑞}𝑋_{𝑞 }… (9)}$$
其中，
$$\mathrm{𝑋_{𝑑} = 𝑋_{𝑙} + 𝑋_{𝑎𝑑}\:\:\:and \:\:\:𝑋_{𝑞} = 𝑋_{𝑙} + 𝑋_{𝑎𝑞}}$$
電抗$𝑋_{𝑑}$稱為**直軸同步電抗**，電抗$𝑋_{𝑞}$稱為**交軸同步電抗**。
$$\mathrm{∴\:𝑬_{𝑓 }= 𝑽 + Ｉ_{𝑎}𝑅_{𝑎} + 𝑗Ｉ_{𝑑}𝑋_{𝑑} + 𝑗Ｉ_{𝑞}𝑋_{𝑞} … (10)}$$
公式(10)是凸極同步發電機電壓方程的最終形式。
相量圖
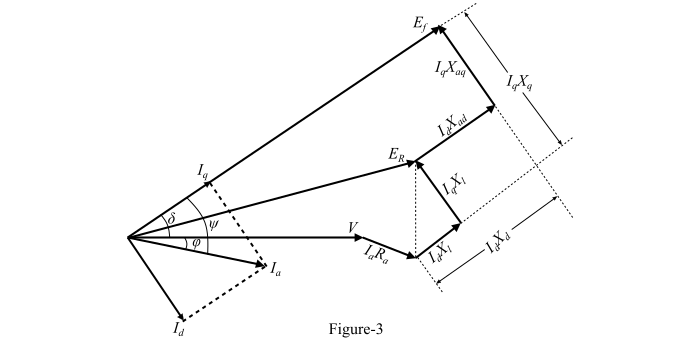
圖3顯示了基於Blondel雙反應理論的凸極同步發電機的完整相量圖。
14K+ 瀏覽量
