SymPy 快速指南

---

---

SymPy - 簡介

SymPy 是一個用於執行符號計算的 Python 庫。它是一個計算機代數系統 (CAS)，可以作為獨立應用程式使用，也可以作為其他應用程式的庫使用。它的即時會話也提供在 https://live.sympy.org/。因為它是一個純 Python 庫，所以它可以作為互動模式和程式化應用程式使用。SymPy 現在已成為科學 Python 生態系統中流行的符號庫。

SymPy 具有廣泛的功能，適用於基礎符號算術、微積分、代數、離散數學、量子物理學等領域。SymPy 能夠以多種格式（包括 LaTeX、MathML 等）格式化結果。SymPy 在 New BSD 許可下發布。由Ondřej Čertík 和Aaron Meurer領導的開發團隊於 2007 年釋出了 SymPy 的第一個版本。其當前版本為 1.5.1。

SymPy 的一些應用領域包括：

• 多項式
• 微積分
• 離散數學
• 矩陣
• 幾何
• 繪圖
• 物理
• 統計
• 組合數學

SymPy - 安裝

SymPy 有一個重要的先決條件庫，名為mpmath。它是一個用於任意精度實數和複數浮點運算的 Python 庫。但是，Python 的包安裝程式 PIP 會在安裝 SymPy 時自動安裝它，如下所示：

pip install sympy

其他 Python 發行版，如 Anaconda、Enthought Canopy 等，可能已經捆綁了 SymPy。要驗證，您可以在 Python 提示符下鍵入以下內容：

>>> import sympy
>>> sympy.__version__

您將獲得以下輸出作為 sympy 的當前版本：

'1.5.1'

SymPy 包的原始碼可在 https://github.com/sympy/sympy 獲取。

SymPy - 符號計算

符號計算是指開發用於運算元學表示式和其他數學物件的演算法。符號計算將數學與計算機科學相結合，使用數學符號求解數學表示式。像 SymPy 這樣的計算機代數系統 (CAS) 使用與傳統手動方法中使用的相同符號精確地（而不是近似地）計算代數表示式。例如，我們使用 Python 的 math 模組計算數字的平方根，如下所示：

>>> import math 
>>> print (math.sqrt(25), math.sqrt(7))

上述程式碼片段的輸出如下：

5.0 2.6457513110645907

如您所見，7 的平方根是近似計算的。但在 SymPy 中，預設情況下，非完全平方數的平方根保持未計算，如下所示：

>>> import sympy 
>>> print (sympy.sqrt(7))

上述程式碼片段的輸出如下：

sqrt(7)

可以使用下面的程式碼片段來符號化地簡化和顯示錶達式的結果：

>>> import math
>>> print (math.sqrt(12))

上述程式碼片段的輸出如下：

3.4641016151377544

您需要使用下面的程式碼片段使用 sympy 執行相同的操作：

##sympy output 
>>> print (sympy.sqrt(12))

其輸出如下：

2*sqrt(3)

在 Jupyter Notebook 中執行時，SymPy 程式碼使用 MathJax 庫以 LatEx 形式呈現數學符號。這在下面的程式碼片段中顯示：

>>> from sympy import * 
>>> x=Symbol ('x') 
>>> expr = integrate(x**x, x) 
>>> expr

在 python shell 中執行上述命令後，將生成以下輸出：

Integral(x**x, x)

它等同於

$\int \mathrm{x}^{x}\,\mathrm{d}x$

非完全平方的平方根可以使用傳統的符號表示為 LaTeX，如下所示：

>>> from sympy import * 
>>> x=7 
>>> sqrt(x)

上述程式碼片段的輸出如下：

$\sqrt7$

像 SymPy 這樣的符號計算系統可以進行各種計算（例如導數、積分和極限，求解方程，使用矩陣），這些計算都是符號化的。SymPy 包具有不同的模組，支援繪圖、列印（如 LATEX）、物理、統計、組合數學、數論、幾何、邏輯等。

SymPy - 數值

SymPy 包中的核心模組包含 Number 類，該類表示原子數。此類有兩個子類：Float 類和 Rational 類。Rational 類由 Integer 類進一步擴充套件。

Float 類表示任意精度的浮點數。

>>> from sympy import Float 
>>> Float(6.32)

上述程式碼片段的輸出如下：

6.32

SymPy 可以將整數或字串轉換為浮點數。

>>> Float(10)

10.0

Float('1.33E5')# scientific notation

133000.0

在轉換為浮點數時，還可以指定精度位數，如下所示：

>>> Float(1.33333,2)

上述程式碼片段的輸出如下：

1.3

一個數 (p/q) 的表示形式表示為 Rational 類的物件，其中 q 為非零數。

>>> Rational(3/4)

上述程式碼片段的輸出如下：

$\frac{3}{4}$

如果將浮點數傳遞給 Rational() 建構函式，它將返回其二進位制表示的底層值

>>> Rational(0.2)

上述程式碼片段的輸出如下：

$\frac{3602879701896397}{18014398509481984}$

對於更簡單的表示，請指定分母限制。

>>> Rational(0.2).limit_denominator(100)

上述程式碼片段的輸出如下：

$\frac{1}{5}$

當將字串傳遞給 Rational() 建構函式時，將返回任意精度的有理數。

>>> Rational("3.65")

上述程式碼片段的輸出如下：

$\frac{73}{20}$

如果傳遞兩個數字引數，也可以獲得 Rational 物件。分子和分母部分作為屬性可用。

>>> a=Rational(3,5) 
>>> print (a) 
>>> print ("numerator:{}, denominator:{}".format(a.p, a.q))

上述程式碼片段的輸出如下：

3/5

分子：3，分母：5

>>> a

上述程式碼片段的輸出如下：

$\frac{3}{5}$

SymPy 中的 Integer 類表示任何大小的整數。建構函式可以接受 Float 或 Rational 數，但小數部分將被丟棄

>>> Integer(10)

上述程式碼片段的輸出如下：

10

>>> Integer(3.4)

上述程式碼片段的輸出如下：

3

>>> Integer(2/7)

上述程式碼片段的輸出如下：

0

SymPy 有一個RealNumber類，它充當 Float 的別名。SymPy 還將 Zero 和 One 定義為單例類，分別可以使用 S.Zero 和 S.One 訪問，如下所示：

>>> S.Zero

輸出如下：

0

>>> S.One

輸出如下：

1

其他預定義的單例數字物件是 Half、NaN、Infinity 和 ImaginaryUnit

>>> from sympy import S 
>>> print (S.Half)

輸出如下：

½

>>> print (S.NaN)

輸出如下：

nan

Infinity 可作為 oo 符號物件或 S.Infinity 使用

>>> from sympy import oo 
>>> oo

上述程式碼片段的輸出如下：

$\infty$

>>> S.Infinity

上述程式碼片段的輸出如下：

$\infty$

ImaginaryUnit 數可以作為 I 符號匯入或作為 S.ImaginaryUnit 訪問，表示 -1 的平方根

>>> from sympy import I 
>>> I

執行上述程式碼片段時，您將獲得以下輸出：

i

>>> S.ImaginaryUnit

上述程式碼片段的輸出如下：

i

>>> from sympy import sqrt 
>>> i=sqrt(-1) 
>>> i*i

執行上述程式碼片段時，您將獲得以下輸出：

-1

SymPy - 符號

Symbol 是 symPy 庫中最重要的類。如前所述，符號計算是用符號完成的。SymPy 變數是 Symbols 類的物件。

Symbol() 函式的引數是一個包含符號的字串，可以將其賦值給變數。

>>> from sympy import Symbol 
>>> x=Symbol('x') 
>>> y=Symbol('y') 
>>> expr=x**2+y**2 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

$x^2 + y^2$

一個符號可以包含多個字母。

>>> s=Symbol('side') 
>>> s**3

上述程式碼片段給出的輸出等效於以下表達式：

$side^3$

SymPy 還具有Symbols()函式，可以一次定義多個符號。字串包含以逗號或空格分隔的變數名稱。

>>> from sympy import symbols 
>>> x,y,z=symbols("x,y,z")

在 SymPy 的 abc 模組中，所有拉丁字母和希臘字母都定義為符號。因此，此方法比例項化 Symbol 物件更方便。

>>> from sympy.abc import x,y,z

但是，名稱C、O、S、I、N、E和Q是預定義的符號。此外，abc 模組中未定義包含多個字母的符號，對於這些符號，應如上所述使用 Symbol 物件。abc 模組定義了可以檢測預設 SymPy 名稱空間中定義的特殊名稱。clash1 包含單個字母，clash2 包含多個字母的衝突符號

>>> from sympy.abc import _clash1, _clash2 
>>> _clash1

上述程式碼片段的輸出如下：

{'C': C, 'O': O, 'Q': Q, 'N': N, 'I': I, 'E': E, 'S': S}

>>> _clash2

上述程式碼片段的輸出如下：

{'beta': beta, 'zeta': zeta, 'gamma': gamma, 'pi': pi}

可以使用類似於 range() 函式的語法定義索引符號。範圍由冒號指示。範圍的型別由冒號右側的字元確定。如果 itr 是一個數字，則所有左側的連續數字都被視為非負起始值。所有右側的連續數字都被視為結束值加 1。

>>> from sympy import symbols 
>>> symbols('a:5')

上述程式碼片段的輸出如下：

(a0, a1, a2, a3, a4)

>>> symbols('mark(1:4)')

上述程式碼片段的輸出如下：

(mark1, mark2, mark3)

SymPy - 替換

對數學表示式執行的最基本操作之一是替換。SymPy 中的 subs() 函式將第一個引數的所有出現替換為第二個引數。

>>> from sympy.abc import x,a 
>>> expr=sin(x)*sin(x)+cos(x)*cos(x) 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

$\sin^2(x)+\cos^2(x)$

>>> expr.subs(x,a)

上述程式碼片段給出的輸出等效於以下表達式：

$\sin^2(a)+\cos^2(a)$

如果我們想計算某個表示式的值，此函式很有用。例如，我們想透過用 5 代替 a 來計算以下表達式的值。

>>> expr=a*a+2*a+5 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

$a^2 + 2a + 5$

expr.subs(a,5)

上述程式碼片段給出以下輸出：

40

>>> from sympy.abc import x 
>>> from sympy import sin, pi 
>>> expr=sin(x) 
>>> expr1=expr.subs(x,pi) 
>>> expr1

上述程式碼片段給出以下輸出：

0

此函式還用於將子表示式替換為另一個子表示式。在以下示例中，b 將被替換為 a+b。

>>> from sympy.abc import a,b 
>>> expr=(a+b)**2 
>>> expr1=expr.subs(b,a+b) 
>>> expr1

上述程式碼片段給出的輸出等效於以下表達式：

$(2a + b)^2$

SymPy - sympify() 函式

sympify() 函式用於轉換任何任意表達式，以便它可以用作 SymPy 表示式。普通 Python 物件（例如整數物件）將轉換為 SymPy。整數等，字串也將轉換為 SymPy 表示式。

>>> expr="x**2+3*x+2" 
>>> expr1=sympify(expr) 
>>> expr1 
>>> expr1.subs(x,2)

上述程式碼片段給出以下輸出：

12

任何 Python 物件都可以轉換為 SymPy 物件。但是，由於轉換內部使用 eval() 函式，因此不應使用未經消毒的表示式，否則會引發 SympifyError。

>>> sympify("x***2")
---------------------------------------------------------------------------

SympifyError: 表示式“無法解析 'x***2'”的 Sympify 失敗，因為引發了異常。

sympify() 函式採用以下引數：* strict：預設為 False。如果設定為 True，則僅轉換已定義顯式轉換型別的型別。否則，將引發 SympifyError。* evaluate：如果設定為 False，則算術和運算子將轉換為其 SymPy 等效項，而無需計算表示式。

>>> sympify("10/5+4/2")

上述程式碼片段給出以下輸出：

4

>>> sympify("10/5+4/2", evaluate=False)

上述程式碼片段給出以下輸出：

$\frac{10}{5}+\frac{4}{2}$

SymPy - evalf() 函式

此函式計算給定數值表示式到給定浮點精度，最多 100 位數字。該函式還採用 subs 引數，這是一個包含符號數值的字典物件。考慮以下表達式

>>> from sympy.abc import r 
>>> expr=pi*r**2 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

$\Pi{r^2}$

要透過用 5 替換 r 來使用 evalf() 函式計算上述表示式

>>> expr.evalf(subs={r:5})

上述程式碼片段給出以下輸出：

78.5398163397448

預設情況下，浮點精度最多為 15 位，可以透過任意數字（最多 100 位）覆蓋。以下表達式計算精度高達 20 位。

>>> expr=a/b 
>>> expr.evalf(20, subs={a:100, b:3})

上述程式碼片段給出以下輸出：

33.333333333333333333

SymPy - lambdify() 函式

lambdify 函式將 SymPy 表示式轉換為 Python 函式。如果需要在一個很大的值範圍內計算表示式，evalf() 函式效率不高。lambdify 的作用類似於 lambda 函式，區別在於它將 SymPy 名稱轉換為給定數值庫的名稱，通常是 NumPy。預設情況下，lambdify 使用 math 標準庫中的實現。

>>> expr=1/sin(x) 
>>> f=lambdify(x, expr) 
>>> f(3.14)

上述程式碼片段給出以下輸出：

627.8831939138764

表示式可能包含多個變數。在這種情況下，lambdify() 函式的第一個引數是變數列表，後面是待計算的表示式。

>>> expr=a**2+b**2 
>>> f=lambdify([a,b],expr) 
>>> f(2,3)

上述程式碼片段給出以下輸出：

13

但是，為了利用 numpy 庫作為數值後端，我們必須將其定義為 lambdify() 函式的引數。

>>> f=lambdify([a,b],expr, "numpy")

我們在上面的函式中使用兩個 numpy 陣列作為引數 a 和 b。對於 numpy 陣列，執行速度相當快。

>>> import numpy 
>>> l1=numpy.arange(1,6) 
>>> l2=numpy.arange(6,11) 
>>> f(l1,l2)

上述程式碼片段給出以下輸出：

array([ 37, 53, 73, 97, 125], dtype=int32)

SymPy - 邏輯表示式

布林函式定義在 **sympy.basic.booleanarg 模組**中。可以使用標準 Python 運算子 &（與）、|（或）、~（非）以及 >> 和 << 來構建布林表示式。布林表示式繼承自 SymPy 核心模組中定義的 Basic 類。

BooleanTrue 函式

此函式等效於核心 Python 中的 True。它返回一個單例，可以透過 S.true 獲取。

>>> from sympy import * 
>>> x=sympify(true) 
>>> x, S.true

上述程式碼片段給出以下輸出：

(True, True)

BooleanFalse 函式

類似地，此函式等效於 Python 中的布林值 False，可以透過 S.false 訪問。

>>> from sympy import * 
>>> x=sympify(false) 
>>> x, S.false

上述程式碼片段給出以下輸出：

(False, False)

And 函式

邏輯 AND 函式計算其兩個引數，如果其中任何一個為 False，則返回 False。該函式模擬 & 運算子。

>>> from sympy import * 
>>> from sympy.logic.boolalg import And 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=True 
>>> And(x,y), x"&"y

上述程式碼片段給出以下輸出：

(True, True)

>>> y=False 
>>> And(x,y), x"&"y

上述程式碼片段給出以下輸出：

(False, False)

Or 函式

此函式計算兩個布林引數，如果其中任何一個為 True，則返回 True。| 運算子方便地模擬了它的行為。

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Or(x,y), x|y

上述程式碼片段給出以下輸出：

(True, True)

>>> x=False 
>>> y=False 
>>> Or(x,y), x|y

上述程式碼片段給出以下輸出：

(False, False)

Not 函式

邏輯非函式導致布林引數取反。如果其引數為 False，則返回 True；如果為 True，則返回 False。~ 運算子執行類似於 Not 函式的操作。如下例所示：

>>> from sympy import * 
>>> from sympy.logic.boolalg import Or, And, Not 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False 
>>> Not(x), Not(y)

上述程式碼片段給出以下輸出：

(False, True)

>>> Not(And(x,y)), Not(Or(x,y))

上述程式碼片段給出以下輸出：

(True, False)

Xor 函式

邏輯異或 (XOR) 函式如果奇數個引數為 True，其餘為 False，則返回 True；如果偶數個引數為 True，其餘為 False，則返回 False。^ 運算子執行類似的操作。

>>> from sympy import * 
>>> from sympy.logic.boolalg import Xor 
>>> x,y=symbols('x y') 
>>> x=True 
>>> y=False

>>> Xor(x,y), x^y

上述程式碼片段給出以下輸出：

(True, True)

>>> a,b,c,d,e=symbols('a b c d e') 
>>> a,b,c,d,e=(True, False, True, True, False) 
>>> Xor(a,b,c,d,e)

上述程式碼片段給出以下輸出：

True

在上述情況下，三個（奇數）引數為 True，因此 Xor 返回 true。但是，如果 True 引數的個數為偶數，則結果為 False，如下所示：

>>> a,b,c,d,e=(True, False, False, True, False) 
>>> Xor(a,b,c,d,e)

上述程式碼片段給出以下輸出：

False

Nand 函式

此函式執行邏輯 NAND 操作。它計算其引數，如果任何一個引數為 False，則返回 True；如果所有引數都為 True，則返回 False。

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nand 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nand(a,b,c), Nand(a,c)

上述程式碼片段給出以下輸出：

(True, False)

Nor 函式

此函式執行邏輯 NOR 操作。它計算其引數，如果任何一個引數為 True，則返回 False；如果所有引數都為 False，則返回 True。

>>> from sympy import * 
>>> from sympy.logic.boolalg import Nor 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Nor(a,b,c), Nor(a,c)

上述程式碼片段給出以下輸出：

(False, False)

請注意，儘管 SymPy 提供了 ^ 運算子用於 Xor，~ 用於 Not，| 用於 Or，& 用於 And 函式作為方便之舉，但它們在 Python 中的常規用法是位運算子。因此，如果運算元是整數，結果將有所不同。

Equivalent 函式

此函式返回等價關係。Equivalent(A, B) 當且僅當 A 和 B 都為 True 或都為 False 時為 True。如果所有引數在邏輯上都等效，則該函式返回 True。否則返回 False。

>>> from sympy import * 
>>> from sympy.logic.boolalg import Equivalent 
>>> a,b,c=symbols('a b c') 
>>> a,b,c=(True, False, True) 
>>> Equivalent(a,b), Equivalent(a,c)

上述程式碼片段給出以下輸出：

(False, True)

ITE 函式

此函式在程式語言中充當 If then else 子句。ITE(A, B, C) 計算並返回 B 的結果（如果 A 為真），否則返回 C 的結果。所有引數必須是布林值。

>>> from sympy import * >>> from sympy.logic.boolalg import ITE >>> a,b,c=symbols('a b c') >>> a,b,c=(True, False, True) 
>>> ITE(a,b,c), ITE(a,c,b)

上述程式碼片段給出以下輸出：

(False, True)

SymPy - 查詢

SymPy 包中的 assumptions 模組包含用於提取有關表示式資訊的工具。該模組為此目的定義了 ask() 函式。

sympy.assumptions.ask(property)

以下屬性提供有關表示式的有用資訊：

algebraic(x)

要成為代數數，一個數必須是非零多項式方程（具有有理係數）的根。√2 是代數數，因為 √2 是 x² - 2 = 0 的解。

complex(x)

複數謂詞。當且僅當 x 屬於複數集時為真。

composite(x)

由 ask(Q.composite(x)) 返回的合數謂詞當且僅當 x 是正整數且至少有一個除 1 和自身以外的正約數時為真。

even, odd

ask() 分別返回 x 是否屬於偶數集和奇數集。

imaginary

此屬性表示虛數謂詞。如果 x 可以寫成實數乘以虛數單位 I，則為真。

integer

Q.integer(x) 返回的此屬性如果 x 屬於偶數集則返回 true。

rational, irrational

Q.irrational(x) 當且僅當 x 是任何不能表示為整數比率的實數時為真。例如，π 是一個無理數。

positive, negative

用於檢查數字是正數還是負數的謂詞

zero, nonzero

用於檢查數字是否為零的謂詞

>>> from sympy import * 
>>> x=Symbol('x') 
>>> x=10 
>>> ask(Q.algebraic(pi))
False
>>> ask(Q.complex(5-4*I)), ask( Q.complex(100))
(True, True)
>>> x,y=symbols("x y") 
>>> x,y=5,10 
>>> ask(Q.composite(x)), ask(Q.composite(y))
(False, True)
>>> ask(Q.even(x)), ask(Q.even(y))
(False, True)
>>> x,y= 2*I, 4+5*I 
>>> ask(Q.imaginary(x)), ask(Q.imaginary(y))
(True, False)
>>> x,y=5,10 
>>> ask(Q.even(x)), ask(Q.even(y)), ask(Q.odd(x)), ask(Q.odd(y))
(False, True, True, False)
>>> x,y=5,-5 
>>> ask(Q.positive(x)), ask(Q.negative(y)), ask(Q.positive(x)), ask(Q.negative(y))
(True, True, True, True)
>>> ask(Q.rational(pi)), ask(Q.irrational(S(2)/3))
(False, False)
>>> ask(Q.zero(oo)), ask(Q.nonzero(I))
(False, False)

SymPy - 簡化

SymPy 具有強大的簡化數學表示式的能力。SymPy 中有許多函式可以執行各種簡化。有一個名為 simplify() 的通用函式，它嘗試得到表示式最簡單的形式。

simplify

此函式定義在 sympy.simplify 模組中。simplify() 嘗試應用智慧啟發式方法來使輸入表示式“更簡單”。以下程式碼顯示了簡化表示式 sin²(x) + cos²(x)。

>>> from sympy import * 
>>> x=Symbol('x')
>>> expr=sin(x)**2 + cos(x)**2 
>>> simplify(expr)

上述程式碼片段給出以下輸出：

1

expand

expand() 是 SymPy 中最常見的簡化函式之一，用於展開多項式表示式。例如：

>>> a,b=symbols('a b') 
>>> expand((a+b)**2)

上述程式碼片段給出的輸出等效於以下表達式：

a² + 2ab + b²

>>> expand((a+b)*(a-b))

上述程式碼片段給出的輸出等效於以下表達式：

a² - b²

expand() 函式使表示式變大，而不是變小。通常情況下是這樣，但有時在呼叫 expand() 後，表示式會變小。

>>> expand((x + 1)*(x - 2) - (x - 1)*x)

上述程式碼片段給出以下輸出：

-2

factor

此函式接受一個多項式並將其分解為有理數上的不可約因子。

>>> x,y,z=symbols('x y z') 
>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor(expr)

上述程式碼片段給出的輸出等效於以下表達式：

z(x + 2y)²

>>> factor(x**2+2*x+1)

上述程式碼片段給出的輸出等效於以下表達式：

(x + 1)²

factor() 函式與 expand() 相反。factor() 返回的每個因子都保證是不可約的。factor_list() 函式返回更結構化的輸出。

>>> expr=(x**2*z + 4*x*y*z + 4*y**2*z) 
>>> factor_list(expr)

上述程式碼片段給出的輸出等效於以下表達式：

(1, [(z, 1), (x + 2*y, 2)])

collect

此函式根據表示式列表收集表示式的加法項，直到具有有理指數的冪。

>>> expr=x*y + x - 3 + 2*x**2 - z*x**2 + x**3 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

x³ + x²z + 2x² + xy + x - 3

對該表示式進行 collect() 函式處理後的結果如下：

>>> collect(expr,x)

上述程式碼片段給出的輸出等效於以下表達式：

x³ + x²(2 - z) + x(y + 1) - 3

>>> expr=y**2*x + 4*x*y*z + 4*y**2*z+y**3+2*x*y 
>>> collect(expr,y)

上述程式碼片段給出的輸出等效於以下表達式：

Y³ + Y²(x + 4z) + y(4xz + 2x)

cancel

cancel() 函式將採用任何有理函式並將其轉換為標準規範形式 p/q，其中 p 和 q 是沒有公因數的展開多項式。p 和 q 的最高次項係數沒有分母，即它們是整數。

>>> expr1=x**2+2*x+1 
>>> expr2=x+1 
>>> cancel(expr1/expr2)

上述程式碼片段給出的輸出等效於以下表達式：

x + 1

>>> expr = 1/x + (3*x/2 - 2)/(x - 4) 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

(3x/2 - 2) / (x - 4) + 1/x

>>> cancel(expr)

上述程式碼片段給出的輸出等效於以下表達式：

(3x² - 2x - 8) / (2x² - 8)

>>> expr=1/sin(x)**2 
>>> expr1=sin(x) 
>>> cancel(expr1*expr)

上述程式碼片段給出的輸出等效於以下表達式：

1/sin(x)

trigsimp

此函式用於簡化三角恆等式。需要注意的是，反三角函式的命名約定是在函式名前新增一個 a。例如，反餘弦或反餘弦稱為 acos()。

>>> from sympy import trigsimp, sin, cos 
>>> from sympy.abc import x, y
>>> expr = 2*sin(x)**2 + 2*cos(x)**2 
>>> trigsimp(expr)

2

trigsimp 函式使用啟發式方法應用最合適的三角恆等式。

powersimp

此函式透過組合具有相似底數和指數的冪來簡化給定表示式。

>>> expr=x**y*x**z*y**z 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

xʸxᶻyᶻ

>>> powsimp(expr)

上述程式碼片段給出的輸出等效於以下表達式：

xʸ⁺ᶻyᶻ

可以透過將 combine='base' 或 combine='exp' 來使 powsimp() 只組合底數或只組合指數。預設情況下，combine='all'，兩者都做。如果 force 為 True，則將在不檢查假設的情況下組合底數。

>>> powsimp(expr, combine='base', force=True)

上述程式碼片段給出的輸出等效於以下表達式：

xʸ(xy)ᶻ

combsimp

包含階乘和二項式的組合表示式可以使用 combsimp() 函式簡化。SymPy 提供了一個 factorial() 函式。

>>> expr=factorial(x)/factorial(x - 3) 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

x! / (x - 3)!

要簡化上述組合表示式，我們使用 combsimp() 函式，如下所示：

>>> combsimp(expr)

上述程式碼片段給出的輸出等效於以下表達式：

x(x - 2)(x - 1)

binomial(x, y) 是從 x 個不同專案集中選擇 y 個專案的方法數。它也常寫成 xCy。

>>> binomial(x,y)

上述程式碼片段給出的輸出等效於以下表達式：

(x/y)

>>> combsimp(binomial(x+1, y+1)/binomial(x, y))

上述程式碼片段給出的輸出等效於以下表達式：

(x + 1) / (y + 1)

logcombine

此函式採用對數並使用以下規則組合它們：

• log(x) + log(y) == log(x*y) （如果兩者都為正）
• a*log(x) == log(x**a) （如果 x 為正且 a 為實數）

>>> logcombine(a*log(x) + log(y) - log(z))

上述程式碼片段給出的輸出等效於以下表達式：

a*log(x) + log(y) - log(z)

如果此函式的 force 引數設定為 True，則如果數量上不存在任何假設，則假定上述假設成立。

>>> logcombine(a*log(x) + log(y) - log(z), force=True)

上述程式碼片段給出的輸出等效於以下表達式：

log(x^a * y / z)

SymPy - 導數

函式的導數是它相對於其一個變數的瞬時變化率。這等效於找到函式在某一點處的切線的斜率。我們可以使用 SymPy 包中的 diff() 函式找到變數形式的數學表示式的微分。

diff(expr, variable)
>>> from sympy import diff, sin, exp 
>>> from sympy.abc import x,y 
>>> expr=x*sin(x*x)+1 >>> expr

上述程式碼片段給出的輸出等效於以下表達式：

x*sin(x²) + 1

>>> diff(expr,x)

上述程式碼片段給出的輸出等效於以下表達式：

2x²cos(x²) + sin(x²)

>>> diff(exp(x**2),x)

上述程式碼片段給出的輸出等效於以下表達式：

2xe^(x²)

要進行多次求導，請根據需要多次傳遞變數，或在變數後傳遞一個數字。

>>> diff(x**4,x,3)

上述程式碼片段給出的輸出等效於以下表達式：

24x

>>> for i in range(1,4): print (diff(x**4,x,i))

上面的程式碼片段給出以下表達式：

4*x**3

12*x**2

24*x

也可以呼叫表示式的 diff() 方法。它的作用與 diff() 函式類似。

>>> expr=x*sin(x*x)+1 
>>> expr.diff(x)

上述程式碼片段給出的輸出等效於以下表達式：

2x²cos(x²) + sin(x²)

使用 Derivative 類建立未計算的導數。它的語法與 diff() 函式相同。要計算未計算的導數，請使用 doit 方法。

>>> from sympy import Derivative 
>>> d=Derivative(expr) 
>>> d

上述程式碼片段給出的輸出等效於以下表達式：

d/dx(x*sin(x²) + 1)

>>> d.doit()

上述程式碼片段給出的輸出等效於以下表達式：

2x²cos(x²) + sin(x²)

SymPy - 積分

SymPy 包包含 integrals 模組。它實現了計算表示式定積分和不定積分的方法。integrate() 方法用於計算定積分和不定積分。要計算不定積分或原函式積分，只需在表示式後傳遞變數即可。

例如：

integrate(f, x)

要計算定積分，請按如下方式傳遞引數：

(integration_variable, lower_limit, upper_limit)

>>> from sympy import * 
>>> x,y = symbols('x y') 
>>> expr=x**2 + x + 1 
>>> integrate(expr, x)

上述程式碼片段給出的輸出等效於以下表達式：

x³/3 + x²/2 + x

>>> expr=sin(x)*tan(x) 
>>> expr 
>>> integrate(expr,x)

上述程式碼片段給出的輸出等效於以下表達式：

-log(sin(x) - 1)/2 + log(sin(x) + 1)/2 - sin(x)

定積分示例如下：

>>> expr=exp(-x**2) 
>>> integrate(expr,(x,0,oo) )

上述程式碼片段給出的輸出等效於以下表達式：

√π/2

您可以傳遞多個極限元組來執行多重積分。示例如下：

>>> expr=exp(-x**2 - y**2)
>>> integrate(expr,(x,0,oo),(y,0,oo))

上述程式碼片段給出的輸出等效於以下表達式：

π/4

您可以使用 Integral 物件建立未計算的積分，可以透過呼叫 doit() 方法來計算它。

>>> expr = Integral(log(x)**2, x) 
>>> expr

上述程式碼片段給出的輸出等效於以下表達式：

∫log(x)²dx

>>> expr.doit()

上述程式碼片段給出的輸出等效於以下表達式：

$x\log(x)^2 - 2x\log(x) + 2x$

積分變換

SymPy 支援多種型別的積分變換，如下所示：

• 拉普拉斯變換 (laplace_transform)
• 傅立葉變換 (fourier_transform)
• 正弦變換 (sine_transform)
• 餘弦變換 (cosine_transform)
• 漢克爾變換 (hankel_transform)

這些函式定義在 sympy.integrals.transforms 模組中。以下示例分別計算傅立葉變換和拉普拉斯變換。

示例 1

>>> from sympy import fourier_transform, exp 
>>> from sympy.abc import x, k 
>>> expr=exp(-x**2) 
>>> fourier_transform(expr, x, k)

在 python shell 中執行上述命令後，將生成以下輸出：

sqrt(pi)*exp(-pi**2*k**2)

等價於：

$\sqrt\pi * e^{\pi^2k^2}$

示例 2

>>> from sympy.integrals import laplace_transform 
>>> from sympy.abc import t, s, a 
>>> laplace_transform(t**a, t, s)

在 python shell 中執行上述命令後，將生成以下輸出：

(s**(-a)*gamma(a + 1)/s, 0, re(a) > -1)

SymPy - 矩陣

在數學中，矩陣是數字、符號或表示式的二維陣列。矩陣操作理論處理對矩陣物件進行算術運算，遵循某些規則。

線性變換是矩陣的重要應用之一。許多科學領域，特別是與物理學相關的領域，都使用與矩陣相關的應用。

SymPy 包含一個 matrices 模組，用於處理矩陣。它包含 Matrix 類，其物件表示一個矩陣。

注意：如果要單獨執行本章中的所有程式碼片段，需要匯入矩陣模組，如下所示：

>>> from sympy.matrices import Matrix

示例

>>> from sympy.matrices import Matrix 
>>> m=Matrix([[1,2,3],[2,3,1]]) 
>>> m
$\displaystyle \left[\begin{matrix}1 & 2 & 3\\2 & 3 & 1\end{matrix}\right]$

在 python shell 中執行上述命令後，將生成以下輸出：

[1 2 3 2 3 1]

矩陣是由大小合適的列表物件建立的。也可以透過將列表項分配到指定數量的行和列來獲得矩陣。

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M
$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

在 python shell 中執行上述命令後，將生成以下輸出：

[10 40 30 2 6 9]

矩陣是可變物件。matrices 模組還提供 ImmutableMatrix 類來獲得不可變矩陣。

基本操作

Matrix 物件的 **shape** 屬性返回其大小。

>>> M.shape

以上程式碼的輸出如下：

(2,3)

row() 和 col() 方法分別返回指定編號的行或列。

>>> M.row(0)
$\displaystyle \left[\begin{matrix}10 & 40 & 30\end{matrix}\right]$

以上程式碼的輸出如下：

[10 40 30]

>>> M.col(1)
$\displaystyle \left[\begin{matrix}40\\6\end{matrix}\right]$

以上程式碼的輸出如下：

[40 6]

使用 Python 的切片運算子來獲取屬於行或列的一個或多個專案。

>>> M.row(1)[1:3]
[6, 9]

Matrix 類具有 row_del() 和 col_del() 方法，可以從給定矩陣中刪除指定行/列：

>>> M=Matrix(2,3,[10,40,30,2,6,9]) 
>>> M.col_del(1) 
>>> M

在 python shell 中執行上述命令後，將生成以下輸出：

Matrix([[10, 30],[ 2, 9]])

可以使用以下命令來設定輸出樣式：

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[10 30 2 9]

>>> M.row_del(0) 
>>> M

$\displaystyle \left[\begin{matrix}2 & 9\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[2 9]

類似地，row_insert() 和 col_insert() 方法在指定的行或列索引處新增行或列。

>>> M1=Matrix([[10,30]]) 
>>> M=M.row_insert(0,M1)
>>> M

$\displaystyle \left[\begin{matrix}10 & 30\\2 & 9\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[10 40 30 2 9]

>>> M2=Matrix([40,6]) 
>>> M=M.col_insert(1,M2) 
>>> M

$\displaystyle \left[\begin{matrix}10 & 40 & 30\\2 & 6 & 9\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[10 40 30 6 9]

算術運算

通常的運算子 +、- 和 * 用於執行加法、減法和乘法。

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5,6],[6,5,4]]) 
>>> M1+M2

$\displaystyle \left[\begin{matrix}5 & 7 & 9\\9 & 7 & 5\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[5 7 9 9 7 5]

>>> M1-M2
$\displaystyle \left[\begin{matrix}-3 & -3 & -3\\-3 & -3 & -3\end{matrix}\right]$

執行以上程式碼片段後，得到以下輸出：

[- 3 -3 -3 -3 -3 -3]

矩陣乘法只有在以下情況下才有可能：第一個矩陣的列數必須等於第二個矩陣的行數。結果將與第一個矩陣具有相同數量的行，與第二個矩陣具有相同數量的列。

>>> M1=Matrix([[1,2,3],[3,2,1]]) 
>>> M2=Matrix([[4,5],[6,6],[5,4]]) 
>>> M1*M2
$\displaystyle \left[\begin{matrix}31 & 29\\29 & 31\end{matrix}\right]$

以上程式碼的輸出如下：

[31 29 29 31]

>>> M1.T
$\displaystyle \left[\begin{matrix}1 & 3\\2 & 2\\3 & 1\end{matrix}\right]$

執行程式碼後得到以下輸出：

[1 3 2 2 3 1]

要計算矩陣的行列式，請使用 det() 方法。行列式是一個標量值，可以根據方陣的元素計算得出。

>>> M=Matrix(3,3,[10,20,30,5,8,12,9,6,15])
>>> M
$\displaystyle \left[\begin{matrix}10 & 20 & 30\\5 & 8 & 12\\9 & 6 & 15\end{matrix}\right]$

以上程式碼的輸出如下：

[10 20 30 5 8 12 9 6 15]

>>> M.det()

以上程式碼的輸出如下：

-120

矩陣構造器

SymPy 提供許多特殊型別的矩陣類。例如，單位矩陣、全零矩陣和全一矩陣等。這些類分別命名為 eye、zeros 和 ones。單位矩陣是一個方陣，對角線上的元素設定為 1，其餘元素為 0。

示例

from sympy.matrices import eye eye(3)

輸出

Matrix([[1, 0, 0], [0, 1, 0], [0, 0, 1]])

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1\end{matrix}\right]$

以上程式碼的輸出如下：

[1 0 0 0 1 0 0 0 1]

在 diag 矩陣中，對角線上的元素根據提供的引數進行初始化。

>>> from sympy.matrices import diag 
>>> diag(1,2,3)

$\displaystyle \left[\begin{matrix}1 & 0 & 0\\0 & 2 & 0\\0 & 0 & 3\end{matrix}\right]$

以上程式碼的輸出如下：

[1 0 0 0 2 0 0 0 3]

zeros 矩陣中的所有元素都初始化為 0。

>>> from sympy.matrices import zeros 
>>> zeros(2,3)

$\displaystyle \left[\begin{matrix}0 & 0 & 0\\0 & 0 & 0\end{matrix}\right]$

以上程式碼的輸出如下：

[0 0 0 0 0 0]

類似地，ones 矩陣的所有元素都設定為 1。

>>> from sympy.matrices import ones
>>> ones(2,3)

$\displaystyle \left[\begin{matrix}1 & 1 & 1\\1 & 1 & 1\end{matrix}\right]$

以上程式碼的輸出如下：

[1 1 1 1 1 1]

SymPy - 函式類

Sympy 包含 Function 類，該類定義在 sympy.core.function 模組中。它是所有應用數學函式的基類，也是未定義函式類的構造器。

以下幾類函式繼承自 Function 類：

• 複數函式
• 三角函式
• 整數函式
• 組合函式
• 其他雜項函式

複數函式

這組函式定義在 **sympy.functions.elementary.complexes** 模組中。

re

此函式返回表示式的實部：

>>> from sympy import * 
>>> re(5+3*I)

以上程式碼片段的輸出如下：

5

>>> re(I)

以上程式碼片段的輸出為：

0

Im

此函式返回表示式的虛部：

>>> im(5+3*I)

以上程式碼片段的輸出如下：

3

>>> im(I)

以上程式碼片段的輸出如下：

1

sign

此函式返回表示式的複數符號。

對於實數表示式，符號將為：

• 1，如果表示式為正
• 0，如果表示式等於零
• -1，如果表示式為負

如果表示式為虛數，則返回的符號為：

• I，如果 im(表示式) 為正
• -I，如果 im(表示式) 為負

>>> sign(1.55), sign(-1), sign(S.Zero)

以上程式碼片段的輸出如下：

(1, -1, 0)

>>> sign (-3*I), sign(I*2)

以上程式碼片段的輸出如下：

(-I, I)

Abs

此函式返回複數的絕對值。它定義為複平面上原點 (0,0) 與點 (a,b) 之間的距離。此函式是內建函式 abs() 的擴充套件，可以接受符號值。

>>> Abs(2+3*I)

以上程式碼片段的輸出如下：

$\sqrt13$

conjugate

此函式返回複數的共軛。要找到複共軛，我們將改變虛部的符號。

>>> conjugate(4+7*I)

執行以上程式碼片段後，得到以下輸出：

4 - 7i

三角函式

SymPy 定義了所有三角比 - sin、cos、tan 等以及其反函式，如 asin、acos、atan 等。這些函式計算給定角度（以弧度表示）的相應值。

>>> sin(pi/2), cos(pi/4), tan(pi/6)

以上程式碼片段的輸出如下：

(1, sqrt(2)/2, sqrt(3)/3)

>>> asin(1), acos(sqrt(2)/2), atan(sqrt(3)/3)

以上程式碼片段的輸出如下：

(pi/2, pi/4, pi/6)

整數函式

這是一組用於對整數執行各種運算的函式。

ceiling

這是一個一元函式，返回不小於其引數的最小整數值。對於複數，分別對實部和虛部取上界。

>>> ceiling(pi), ceiling(Rational(20,3)), ceiling(2.6+3.3*I)

以上程式碼片段的輸出如下：

(4, 7, 3 + 4*I)

floor

此函式返回不大於其引數的最大整數值。對於複數，此函式也分別對實部和虛部取下界。

>>> floor(pi), floor(Rational(100,6)), floor(6.3-5.9*I)

以上程式碼片段的輸出如下：

(3, 16, 6 - 6*I)

frac

此函式表示 x 的小數部分。

>>> frac(3.99), frac(Rational(10,3)), frac(10)

以上程式碼片段的輸出如下：

(0.990000000000000, 1/3, 0)

組合函式

組合數學是數學的一個分支，它關注有限或離散系統中的選擇、排列和運算問題。

factorial

階乘在組合數學中非常重要，它給出 n 個物件可以排列的方式的數量。它在符號上表示為 𝑥! 此函式是在非負整數上的階乘函式的實現，負整數的階乘是復無窮大。

>>> x=Symbol('x') 
>>> factorial(x)

以上程式碼片段的輸出如下：

x!

>>> factorial(5)

以上程式碼片段的輸出如下：

120

>>> factorial(-1)

以上程式碼片段的輸出如下：

$\infty\backsim$

binomial

此函式表示從 n 個元素的集合中選擇 k 個元素的方式的數量。

>>> x,y=symbols('x y') 
>>> binomial(x,y)

以上程式碼片段的輸出如下：

(x/y)

>>> binomial(4,2)

以上程式碼片段的輸出如下：

6

帕斯卡三角形的行可以使用二項式函式生成。

>>> for i in range(5): print ([binomial(i,j) for j in range(i+1)])

執行以上程式碼片段後，得到以下輸出：

[1]

[1, 1]

[1, 2, 1]

[1, 3, 3, 1]

[1, 4, 6, 4, 1]

fibonacci

斐波那契數列是由初始項 F0=0，F1=1 和兩項遞推關係 Fn=Fn−1+Fn−2 定義的整數序列。

>>> [fibonacci(x) for x in range(10)]

執行以上程式碼片段後得到以下輸出：

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34]

tribonacci

特里波那契數列是由初始項 F0=0，F1=1，F2=1 和三項遞推關係 Fn=Fn-1+Fn-2+Fn-3 定義的整數序列。

>>> tribonacci(5, Symbol('x'))

上述程式碼片段給出的輸出等效於以下表達式：

$x^8 + 3x^5 + 3x^2$

>>> [tribonacci(x) for x in range(10)]

執行以上程式碼片段後得到以下輸出：

[0, 1, 1, 2, 4, 7, 13, 24, 44, 81]

雜項函式

以下是某些常用函式的列表：

**Min** - 返回列表的最小值。它命名為 Min 以避免與內建函式 min 衝突。

**Max** - 返回列表的最大值。它命名為 Max 以避免與內建函式 max 衝突。

**root** - 返回 x 的 n 次方根。

**sqrt** - 返回 x 的主平方根。

**cbrt** - 此函式計算 x 的主立方根（x++Rational(1,3) 的快捷方式）。

以下是上述雜項函式及其各自輸出的示例：

>>> Min(pi,E)

e

>>> Max(5, Rational(11,2))

$\frac{11}{2}$

>>> root(7,Rational(1,2))

49

>>> sqrt(2)

$\sqrt2$

>>> cbrt(1000)

10

SymPy - 四元數

在數學中，四元數系統是複數的擴充套件。每個四元數物件包含四個標量變數和四個維度，一個實數維度和三個虛數維度。

四元數由以下表達式表示：

q=a+bi+cj+dk

其中 **a、b、c** 和 d 是實數，**i、j、k** 是四元數單位，使得 i2==j2==k2==ijk

**sympy.algebras.quaternion** 模組具有 Quaternion 類。

>>> from sympy.algebras.quaternion import Quaternion 
>>> q=Quaternion(2,3,1,4) 
>>> q

上述程式碼片段給出的輸出等效於以下表達式：

$2 + 3i + 1j + 4k$

四元數用於純數學以及應用數學、計算機圖形學、計算機視覺等。

>>> from sympy import * 
>>> x=Symbol('x') 
>>> q1=Quaternion(x**2, x**3, x) >>> q1

上述程式碼片段給出的輸出等效於以下表達式：

$x^2 + x^3i + xj + 0k$

四元數物件也可以具有虛係數

>>> q2=Quaternion(2,(3+2*I), x**2, 3.5*I) 
>>> q2

上述程式碼片段給出的輸出等效於以下表達式：

$2 + (3 + 2i)i + x2j + 3.5ik$

add()

此方法在 Quaternion 類中可用，用於執行兩個 Quaternion 物件的加法。

>>> q1=Quaternion(1,2,3,4) 
>>> q2=Quaternion(4,3,2,1) 
>>> q1.add(q2)

上述程式碼片段給出的輸出等效於以下表達式：

$5 + 5i + 5j + 5k$

可以在四元數物件中新增數字或符號。

>>> q1+2

執行以上程式碼片段後得到以下輸出：

$3 + 2i + 3j + 4k$

>>> q1+x

執行以上程式碼片段後得到以下輸出：

$(x + 1) + 2i + 3j + 4k$

mul()

此方法執行兩個四元數物件的乘法。

>>> q1=Quaternion(1,2,1,2) 
>>> q2=Quaternion(2,4,3,1) 
>>> q1.mul(q2)

上述程式碼片段給出的輸出等效於以下表達式：

$(-11) + 3i + 11j + 7k$

inverse()

此方法返回四元數物件的逆。

>>> q1.inverse()

上述程式碼片段給出的輸出等效於以下表達式：

$\frac{1}{10} + (-\frac{1}{5})i + (-\frac{1}{10})j + (-\frac{1}{5})k$

pow()

此方法返回四元數物件的冪。

>>> q1.pow(2)

執行以上程式碼片段後得到以下輸出：

$(-8) + 4i + 2j + 4k$

exp()

此方法計算四元數物件的指數，即 eq

>>> q=Quaternion(1,2,4,3) 
>>> q.exp()

執行以上程式碼片段後得到以下輸出：

$e\cos(\sqrt29) + \frac{2\sqrt29e\sin(\sqrt29)}{29}i + \frac{4\sqrt29e\sin(\sqrt29)}{29}j + \frac{3\sqrt29e\sin}{29}k$

SymPy - 求解器

由於符號 = 和 == 在 Python 中定義為賦值運算子和相等運算子，因此它們不能用於制定符號方程。SymPy 提供 Eq() 函式來建立方程。

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> Eq(x,y)

上述程式碼片段給出的輸出等效於以下表達式：

x = y

由於當且僅當 x-y=0 時 x=y 成立，因此上述方程可以寫成：

>>> Eq(x-y,0)

上述程式碼片段給出的輸出等效於以下表達式：

x − y = 0

SymPy 中的 solver 模組提供 solveset() 函式，其原型如下：

solveset(equation, variable, domain)

預設情況下，域為 S.Complexes。使用 solveset() 函式，可以如下求解代數方程：

>>> solveset(Eq(x**2-9,0), x)

獲得以下輸出：

{−3, 3}

>>> solveset(Eq(x**2-3*x, -2),x)

執行以上程式碼片段後得到以下輸出：

{1,2}

solveset 的輸出是解的 FiniteSet。如果沒有解，則返回 EmptySet

>>> solveset(exp(x),x)

執行以上程式碼片段後得到以下輸出：

$\varnothing$

線性方程

我們必須使用 linsolve() 函式來求解線性方程。

例如，方程如下：

x-y=4

x+y=1

>>> from sympy import * 
>>> x,y=symbols('x y') 
>>> linsolve([Eq(x-y,4),Eq( x + y ,1) ], (x, y))

執行以上程式碼片段後得到以下輸出：

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

linsolve() 函式也可以求解以矩陣形式表示的線性方程。

>>> a,b=symbols('a b') 
>>> a=Matrix([[1,-1],[1,1]]) 
>>> b=Matrix([4,1]) 
>>> linsolve([a,b], (x,y))

如果執行以上程式碼片段，我們將得到以下輸出：

$\lbrace(\frac{5}{2},-\frac{3}{2})\rbrace$

非線性方程

為此，我們使用 nonlinsolve() 函式。此示例的方程：

a²+a=0 a-b=0

>>> a,b=symbols('a b') 
>>> nonlinsolve([a**2 + a, a - b], [a, b])

如果執行以上程式碼片段，我們將得到以下輸出：

$\lbrace(-1, -1),(0,0)\rbrace$

微分方程

首先，透過將 cls=Function 傳遞給 symbols 函式來建立一個未定義的函式。要求解微分方程，請使用 dsolve。

>>> x=Symbol('x') 
>>> f=symbols('f', cls=Function) 
>>> f(x)

執行以上程式碼片段後得到以下輸出：

f(x)

這裡 f(x) 是一個未計算的函式。其導數如下：

>>> f(x).diff(x)

上述程式碼片段給出的輸出等效於以下表達式：

$\frac{d}{dx}f(x)$

我們首先建立與以下微分方程對應的 Eq 物件

>>> eqn=Eq(f(x).diff(x)-f(x), sin(x)) 
>>> eqn

上述程式碼片段給出的輸出等效於以下表達式：

$-f(x) + \frac{d}{dx}f(x)= \sin(x)$

>>> dsolve(eqn, f(x))

上述程式碼片段給出的輸出等效於以下表達式：

$f(x)=(c^1-\frac{e^-x\sin(x)}{2}-\frac{e^-x\cos(x)}{2})e^x$

SymPy - 繪圖

SymPy 使用 Matplotlib 庫作為後端來渲染數學函式的二維和三維圖。確保當前 Python 安裝中可以使用 Matplotlib。如果不是，請使用以下命令安裝：

pip install matplotlib

繪圖支援定義在 sympy.plotting 模組中。繪圖模組中存在以下函式：

• **plot** - 二維線圖

• **plot3d** - 三維線圖

• **plot_parametric** - 二維引數圖

• **plot3d_parametric** - 三維引數圖

plot() 函式返回 Plot 類的例項。一個繪圖圖形可以有一個或多個 SymPy 表示式。雖然它能夠使用 Matplotlib 作為後端，但也可以使用其他後端，例如 texplot、pyglet 或 Google charts API。

plot(expr, range, kwargs)

其中 expr 是任何有效的 symPy 表示式。如果沒有提及，則範圍使用預設值 (-10, 10)。

以下示例繪製範圍 (-10,10) 中每個值的 x2 值：

>>> from sympy.plotting import plot 
>>> from sympy import * 
>>> x=Symbol('x') 
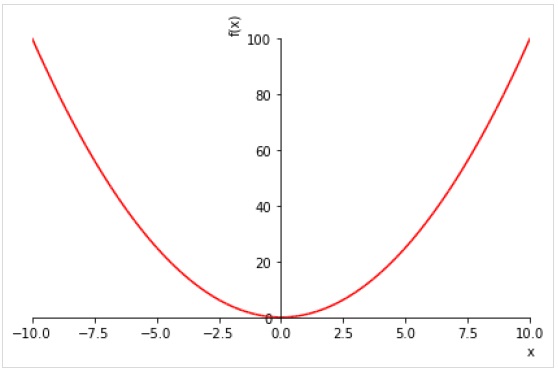
>>> plot(x**2, line_color='red')

要繪製同一範圍內的多個圖形，請在範圍元組之前給出多個表示式。

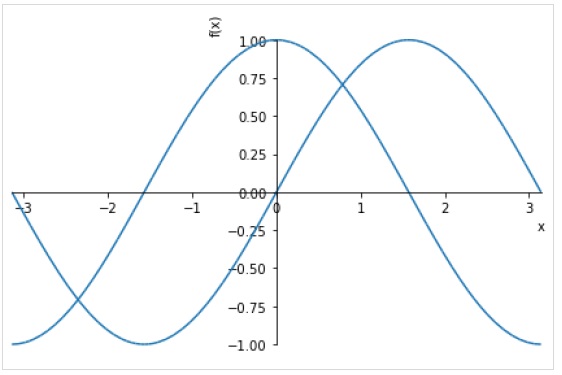
>>> plot( sin(x),cos(x), (x, -pi, pi))

您也可以為每個表示式指定單獨的範圍。

plot((expr1, range1), (expr2, range2))

下圖在不同範圍內繪製了 sin(x) 和 cos(x)。

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)))

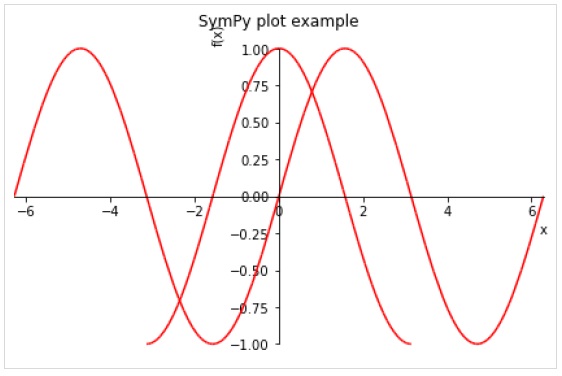
可以在 plot() 函式中指定以下可選關鍵字引數。

• line_color − 指定繪圖線的顏色。

• title − 要顯示為標題的字串

• xlabel − 要顯示為 X 軸標籤的字串

• ylabel − 要顯示為 y 軸標籤的字串

>>> plot( (sin(x),(x, -2*pi, 2*pi)),(cos(x), (x, -pi, pi)), line_color='red', title='SymPy plot example')

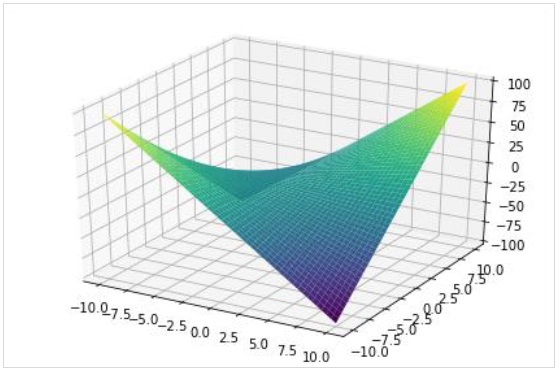
plot3d() 函式渲染三維圖形。

plot3d(expr, xrange, yrange, kwargs)

以下示例繪製了一個 3D 表面圖：

>>> from sympy.plotting import plot3d 
>>> x,y=symbols('x y') 
>>> plot3d(x*y, (x, -10,10), (y, -10,10))

與二維圖形一樣，三維圖形也可以有多個圖形，每個圖形都有不同的範圍。

>>> plot3d(x*y, x/y, (x, -5, 5), (y, -5, 5))

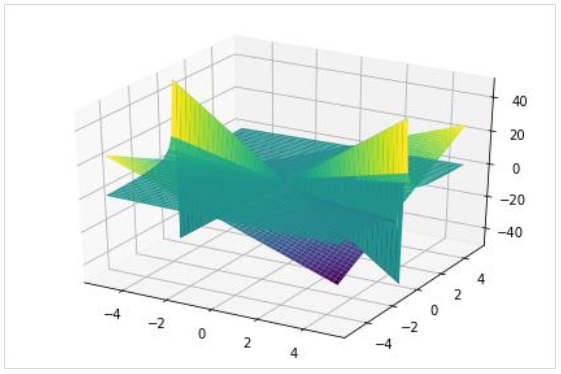
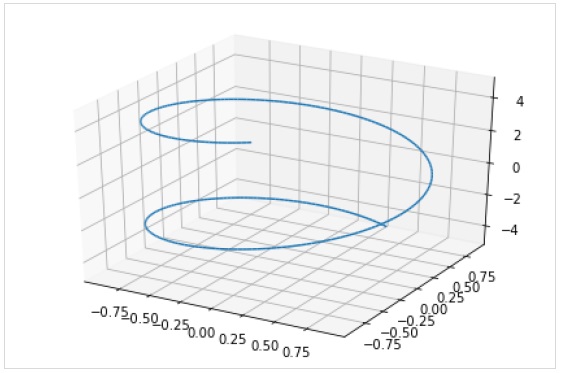
plot3d_parametric_line() 函式渲染三維引數線圖。

>>> from sympy.plotting import plot3d_parametric_line 
>>> plot3d_parametric_line(cos(x), sin(x), x, (x, -5, 5))

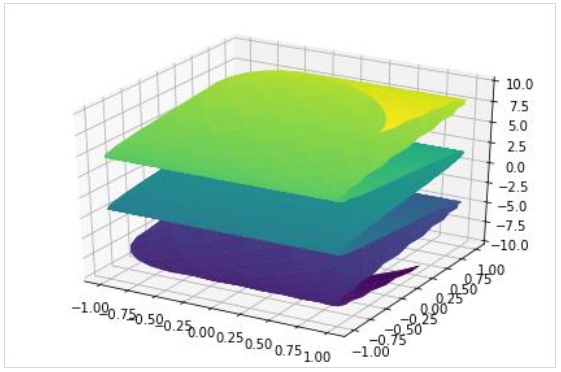
要繪製引數曲面圖，請使用 plot3d_parametric_surface() 函式。

plot3d_parametric_surface(xexpr, yexpr, zexpr, rangex, rangey, kwargs)

>>> from sympy.plotting import plot3d_parametric_surface 
>>> plot3d_parametric_surface(cos(x+y), sin(x-y), x-y, (x, -5, 5), (y, -5, 5))

SymPy - 實體

SymPy 中的 geometry 模組允許建立二維實體，例如線、圓等。然後，我們可以獲得有關它們的的資訊，例如檢查共線性或查詢交點。

點

Point 類表示歐幾里得空間中的一個點。以下示例檢查點的共線性：

>>> from sympy.geometry import Point 
>>> from sympy import * 
>>> x=Point(0,0) 
>>> y=Point(2,2) 
>>> z=Point(4,4) 
>>> Point.is_collinear(x,y,z)

輸出

True

>>> a=Point(2,3) 
>>> Point.is_collinear(x,y,a)

輸出

False

Point 類的 distance() 方法計算兩點之間的距離

>>> x.distance(y)

輸出

$2\sqrt2$

距離也可以用符號表示。

線

線實體是從兩個 Point 物件獲得的。如果兩條線相交，則 intersection() 方法返回交點。

>>> from sympy.geometry import Point, Line 
>>> p1, p2=Point(0,5), Point(5,0) 
>>> l1=Line(p1,p2)
>>> l2=Line(Point(0,0), Point(5,5)) 
>>> l1.intersection(l2)

輸出

[Point2D(5/2, 5/2)]

>>> l1.intersection(Line(Point(0,0), Point(2,2)))

輸出

[Point2D(5/2, 5/2)]

>>> x,y=symbols('x y') 
>>> p=Point(x,y) 
>>> p.distance(Point(0,0))

輸出

$\sqrt{x^2 + y^2}$

三角形

此函式根據三個點物件構建三角形實體。

Triangle(a,b,c)

>>> t=Triangle(Point(0,0),Point(0,5), Point(5,0)) 
>>> t.area

輸出

$-\frac{25}{2}$

橢圓

橢圓幾何實體是透過傳遞對應於中心和兩個數字（每個數字分別對應水平和垂直半徑）的 Point 物件來構造的。

ellipse(center, hradius, vradius)

>>> from sympy.geometry import Ellipse, Line 
>>> e=Ellipse(Point(0,0),8,3) 
>>> e.area

輸出

$24\pi$

可以使用偏心率引數間接提供 vradius。

>>> e1=Ellipse(Point(2,2), hradius=5, eccentricity=Rational(3,4)) 
>>> e1.vradius

輸出

$\frac{5\sqrt7}{4}$

橢圓的遠拱點是焦點和輪廓之間最大的距離。

>>> e1.apoapsis

輸出

$\frac{35}{4}$

以下語句計算橢圓的周長：

>>> e1.circumference

輸出

$20E(\frac{9}{16})$

橢圓的equation方法返回橢圓的方程。

>>> e1.equation(x,y)

輸出

$(\frac{x}{5}-\frac{2}{5})^2 + \frac{16(y-2)^2}{175} - 1$

SymPy - 集合

在數學中，集合是不同物件的明確定義的集合，這些物件可以是數字、人、字母表中的字母，甚至是其他集合。集合也是 Python 中的內建型別之一。SymPy 提供了 sets 模組。它包含不同型別集合的定義，並具有執行集合運算（例如交集、並集等）的功能。

Set 是 SymPy 中任何其他型別集合的基類。請注意，它與 Python 的內建集合資料型別不同。Interval 類表示實數區間，其邊界屬性返回一個FiniteSet物件。

>>> from sympy import Interval 
>>> s=Interval(1,10).boundary 
>>> type(s)

sympy.sets.sets.FiniteSet

FiniteSet 是離散數字的集合。可以從任何序列物件（例如列表或字串）獲得它。

>>> from sympy import FiniteSet 
>>> FiniteSet(range(5))

輸出

$\lbrace\lbrace0,1,...,4\rbrace\rbrace$

>>> numbers=[1,3,5,2,8] 
>>> FiniteSet(*numbers)

輸出

$\lbrace1,2,3,5,8\rbrace$

>>> s="HelloWorld" 
>>> FiniteSet(*s)

輸出

{H,W,d,e,l,o,r}

請注意，與內建集合一樣，SymPy 的 Set 也是不同物件的集合。

ConditionSet 是滿足給定條件的元素的集合

>>> from sympy import ConditionSet, Eq, Symbol 
>>> x=Symbol('x') 
>>> s=ConditionSet(x, Eq(x**2-2*x,0), Interval(1,10)) >>> s

輸出

$\lbrace x\mid x\in[1,10]∧x^2 - 2x =0\rbrace$

Union 是一個複合集合。它包含兩個集合中的所有元素。請注意，在兩者中都找到的元素在 Union 中只會出現一次。

>>> from sympy import Union 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Union(a,b)

另一方面，Intersection 只包含同時存在於兩者的元素。

>>> from sympy import Intersection 
>>> Intersection(a,b)

ProductSet 物件表示兩個集合中元素的笛卡爾積。

>>> from sympy import ProductSet 
>>> l1=[1,2] 
>>> l2=[2,3] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> set(ProductSet(a,b))

Complement(a,b) 保留集合 a 中的元素，但不包括與集合 b 共有的元素。

>>> from sympy import Complement 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> Complement(a,b), Complement(b,a)

SymmetricDifference 集合僅包含兩個集合中不共有的元素。

>>> from sympy import SymmetricDifference 
>>> l1=[3,1,5,7] 
>>> l2=[9,7,2,1] 
>>> a=FiniteSet(*l1) 
>>> b=FiniteSet(*l2) 
>>> SymmetricDifference(a,b)

輸出

{2,3,5,9}

SymPy - 列印

SymPy 中有幾個可用的印表機。以下是部分列表：

• str
• srepr
• ASCII 美化印表機
• Unicode 美化印表機
• LaTeX
• MathML
• Dot

SymPy 物件也可以作為各種語言（例如 C、Fortran、Javascript、Theano 和 Python）程式碼的輸出傳送。

SymPy 使用 Unicode 字元以美化列印的形式呈現輸出。如果您使用 Python 控制檯執行 SymPy 會話，則最佳美化列印環境是透過呼叫 init_session() 函式啟用的。

>>> from sympy import init_session 
>>> init_session()

用於 SymPy 1.5.1 的 IPython 控制檯（Python 3.7.4-64 位）（地面型別：python）。

執行了這些命令：

>>> from __future__ import division
>>> from sympy import *
>>> x, y, z, t = symbols('x y z t')
>>> k, m, n = symbols('k m n', integer=True)
>>> f, g, h = symbols('f g h', cls=Function)
>>> init_printing()

文件可在 https://docs.sympy.org/1.5.1/. 找到。

>>> Integral(sqrt(1/x),x)

$\int \sqrt\frac{1}{x} dx$

如果未安裝 LATEX，但已安裝 Matplotlib，它將使用 Matplotlib 渲染引擎。如果未安裝 Matplotlib，它將使用 Unicode 美化印表機。但是，Jupyter notebook 使用 MathJax 渲染 LATEX。

在不支援 Unicode 的終端中，將使用 ASCII 美化印表機。

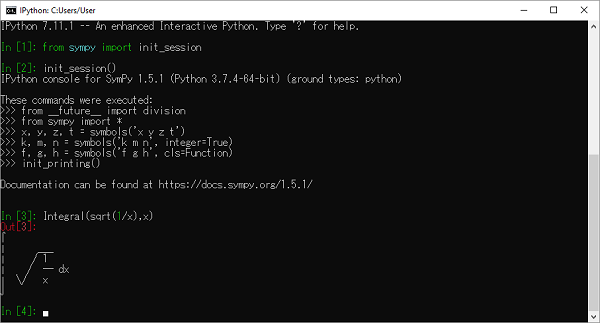
要使用 ASCII 印表機，請將 use_unicode 屬性設定為 False，然後使用 pprint() 函式。

>>> pprint(Integral(sqrt(1/x),x),use_unicode=False)

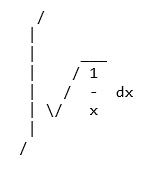
Unicode 美化印表機也可以從 pprint() 和 pretty() 訪問。如果終端支援 Unicode，則會自動使用它。如果 pprint() 無法檢測到終端支援 unicode，則可以傳遞 use_unicode=True 以強制其使用 Unicode。

要獲得表示式的 LATEX 形式，請使用 latex() 函式。

>>> print(latex(Integral(sqrt(1/x),x)))

\int \sqrt{\frac{1}{x}}\, dx

您也可以使用 mathml 印表機。為此，請匯入 print_mathml 函式。字串版本由 mathml() 函式獲得。

>>> from sympy.printing.mathml import print_mathml 
>>> print_mathml(Integral(sqrt(1/x),x))

<apply>

<int/>

<bvar>

<ci>x</ci>

</bvar>

<apply>

<root/>

<apply>

<power/>

<ci>x</ci>

<cn>-1</cn>

</apply>

</apply>

</apply>

>>>mathml(Integral(sqrt(1/x),x))

'<apply><int/><bvar><ci>x</ci></bvar><apply><root/><apply><power/><ci>x</ci><cn>-1</cn></apply></apply></apply>'