資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學靜電感應電動勢和動態感應電動勢
感應電動勢
當穿過導體或線圈的磁通量發生變化時，導體或線圈中就會感應出電動勢，這被稱為感應電動勢。根據改變磁通量的方式，感應電動勢分為兩種：
- 靜電感應電動勢
- 動態感應電動勢
靜電感應電動勢
當導體靜止而磁場變化時，以這種方式感應的電動勢稱為靜電感應電動勢（如在變壓器中）。之所以這樣稱呼，是因為電動勢是在靜止的導體中感應的。靜電感應電動勢還可以分為兩類：
- 靜電感應電動勢
- 互感電動勢
自感電動勢
當由於線圈自身與其相關的磁通量變化而線上圈中感應出電動勢時，這被稱為自感電動勢。
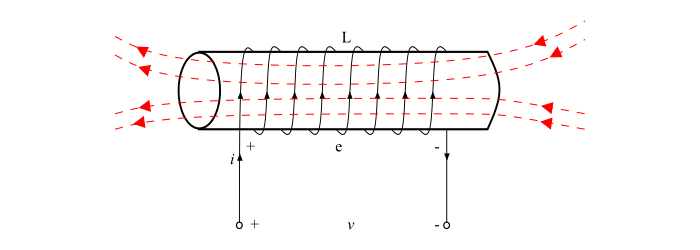
解釋 - 當電流流過線圈時，由該電流產生的磁場穿過線圈。如果線圈中的電流發生變化，則與線圈相關的磁場也會發生變化。因此，根據法拉第電磁感應定律，線圈中會感應出電動勢。這種感應電動勢稱為自感電動勢。
在數學上，自感電動勢由下式給出：
$$\mathrm{e=L\frac{di}{dt}\:\:\:\:\:\:...(1)}$$
其中，L 是線圈的自感。
互感電動勢
當由於相鄰線圈的磁通量變化而線上圈中感應出電動勢時，這被稱為互感電動勢。
解釋 - 考慮兩個彼此相鄰放置的線圈線圈-1 和線圈-2（見圖）。線圈-1產生的磁通量的一部分與線圈-2相連。這兩種線圈1和2共有的磁通量稱為互感磁通量 $(\varphi_{m})$。現在，如果線圈-1中的電流發生變化，則互感磁通量也會發生變化，從而線上圈中感應出電動勢。線圈-2中感應的電動勢稱為互感電動勢，因為它是由線圈-1產生的磁通量變化引起的。在數學上，互感電動勢由下式給出：
$$\mathrm{e_{m}=M\frac{di_{1}}{dt}\:\:\:\:\:\:...(2)}$$
其中，M 是線圈之間的互感。
動態感應電動勢
當導體在靜止磁場中移動，使得與其相關的磁通量的大小發生變化時，由於導體受到變化的磁場作用，因此會在其中感應出電動勢。以這種方式感應的電動勢稱為動態感應電動勢（如在直流或交流發電機中）。之所以這樣稱呼，是因為電動勢是在運動的（動態的）導體中感應的。
解釋 - 考慮一根長度為l 米的導體，它以 v m/s 的速度垂直於磁通密度為 B Wb/m2 的均勻靜止磁場運動。設導體在時間dt 秒內移動一小段距離dx。然後，
$$\mathrm{導體掃過的面積,\mathit{a = l \times dx}\: \:m^{2}}$$
$$\mathrm{\therefore 導體切割的磁通量,\mathit{dψ}= 磁通密度 \:\times\: 掃過的面積}$$
$$\mathrm{\Longrightarrow \mathit{dψ=B \:l\:dx}\: \:Wb}$$
現在，根據法拉第電磁感應定律，感應電動勢將是：
$$\mathrm{\mathit{e=N\frac{dψ}{dt}=\frac{B\:l\:dx}{dt}\: (\because N}=1)}$$
$$\mathrm{\because \mathit{\frac{dx}{dt}}=速度 \mathit{V}}$$
$$\mathrm{\therefore \mathit{e=B\: l\:v}\: \:伏特\:\:\:\:\:\:...(3)}$$
公式 (3) 給出了導體垂直於磁場運動時的動態感應電動勢。
如果導體與磁場成θ角運動，則僅由於速度垂直於磁場的分量而感應的電動勢。
$$\mathrm{\mathit{e=B\:l\:v} \:sinθ\:\:\:\:\:\:...(4)}$$
數值例子
一根長度為 0.8 米的導體位於磁通密度為 2 $Wb/m^{2}$ 的均勻磁場中，並且與磁場成直角。導體以 30 m/s 的速度移動。計算導體中感應的電動勢。如果導體與磁場成 45° 角移動，則感應的電動勢是多少？
解答
情況 1 - 當導體垂直於磁場運動時。
$$\mathrm{\mathit{e=B\:l\:v}=2\times(0.8)\times(30)=48V}$$
情況 2 - 當導體與磁場成 45° 角運動時。
$$\mathrm{\mathit{e=B\:l\:v}\:sinθ=2\times(0.8)\times(30)\times sin45=33.95V}$$
26K+ 瀏覽量
