資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究三相感應電機轉子頻率、電動勢、電流和功率因數
轉子電流頻率
三相感應電機的定子電流和電壓頻率必須與電源頻率相同，由下式給出：
$$\mathrm{𝑓 =\frac{𝑁_{𝑆}𝑃}{120}… (1)}$$
但是，三相感應電機轉子電路中電流和電動勢的頻率是可變的，取決於同步速度(NS)和轉子速度(Nr)之間的差，即取決於滑差。因此，轉子頻率由下式給出：
$$\mathrm{𝑓_{𝑟} =\frac{(𝑁_{𝑆} − 𝑁_{𝑟} )𝑃}{120}… (2)}$$
現在，根據公式 (1) 和 (2)，我們得到：
$$\mathrm{\frac{𝑓_{𝑟}}{𝑓}=\frac{𝑁_{𝑆} − 𝑁_{𝑟}}{𝑁_{𝑆}}}$$
$$\mathrm{∵ 滑差，𝑠 =\frac{𝑁_{𝑆} − 𝑁_{𝑟}}{𝑁_{𝑆}}}$$
$$\mathrm{∴ 𝑓_{𝑟} = 𝑠𝑓 … (3)}$$
即，轉子電流頻率 = 每單位滑差 × 電源頻率 當轉子靜止時，即 Nr = 0，則：
$$\mathrm{𝑠 =\frac{𝑁_{𝑆} − 𝑁_{𝑟}}{𝑁_{𝑆}}= 1}$$
$$\mathrm{∴ 𝑓_{𝑟} = 𝑓}$$
因此，當轉子靜止時，轉子電流的頻率 (fr) 與電源頻率 (f) 相同。
當轉子加速時，旋轉磁場與轉子之間的相對速度減小。結果，滑差 (s) 以及轉子電流頻率減小。
在同步速度下，即Nr = NS，
$$\mathrm{𝑠 =\frac{𝑁_{𝑆} − 𝑁_{𝑟}}{𝑁_{𝑆}}= 0}$$
$$\mathrm{∴ 𝑓_{𝑟} = 0}$$
轉子電動勢
當轉子靜止時，三相感應電機表現為次級繞組短路的變壓器。因此，轉子（或次級）中每相感應電動勢由下式給出：
$$\mathrm{轉子每相電動勢，𝐸_{2} = 𝐸_{1} × \frac{𝑁_{2}}{𝑁_{1}}= 𝐾\:𝐸_{1} … (3)}$$
其中：
- E1 = 定子每相電壓。
- N1 = 定子每相繞組匝數。
- N2 = 轉子每相繞組匝數。
當轉子以滑差 's' 執行時，定子旋轉磁場與轉子之間的相對速度為(NS – Nr)。因此，轉子電動勢與(NS – Nr) 或滑差 (s) 成正比，即：
$$\mathrm{滑差為𝑠時轉子每相電動勢，{𝐸^{′}_{2}} = 𝑠\:𝐾\:𝐸_{1} … (4)}$$
轉子電流和功率因數
考慮下圖所示的任何滑差值 's' 的三相感應電機。
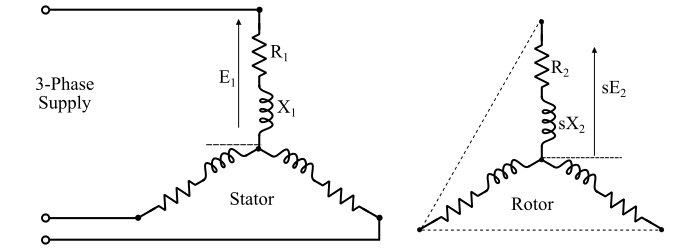
此處，假設轉子為繞線轉子並採用星形連線。因此：
$$\mathrm{轉子每相電動勢，𝐸^{′}_{2} = 𝑠\:𝐸_{2 }\:\:\:(設𝐾 = 1)}$$
$$\mathrm{轉子每相電抗，{𝑋^{′}_{2}} = 𝑠\:𝑋_{2}}$$
其中，X2 是轉子每相電抗的靜止狀態值。
轉子電路的電阻為每相 R2，與頻率無關，因此不依賴於滑差。類似地，定子繞組的電阻 (R1) 和電抗 (X1) 不依賴於滑差。
由於三相感應電機表示平衡的三相負載，因此只需要分析一相，其他兩相的情況相似。
情況 1 – 轉子靜止時
當轉子靜止時，電機處於靜止狀態（滑差，s = 1）
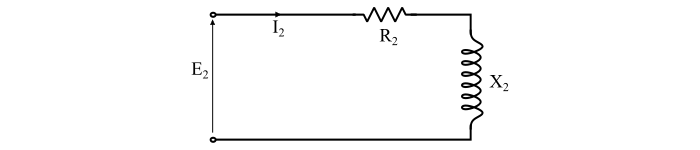
$$\mathrm{轉子每相電流，𝐼_{2} =\frac{𝐸_{2}}{𝑍_{2}}=\frac{𝐸_{2}}{\sqrt{{𝑅_{2}}^{2} + {𝑋_{2}}^{2}}}… (5)}$$
$$\mathrm{轉子功率因數，cos \:φ_{2}=\frac{R_{2}}{𝑍_{2}}=\frac{R_{2}}{\sqrt{{𝑅_{2}}^{2} + {𝑋_{2}}^{2}}}… (6)}$$
情況 2 – 電機以滑差 's' 執行時
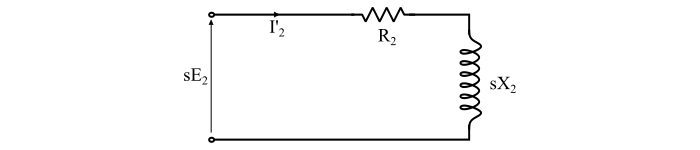
$$\mathrm{轉子每相電流，{𝐼^{′}_{2}}=\frac{𝑠\:𝐸_{2}}{𝑍^{′}_{2}}=\frac{𝑠\:𝐸_{2}}{\sqrt{{R_{2}}^{2} +(SX_{2})^{2}}}}…… (7)$$
$$\mathrm{轉子功率因數，cos\:{φ^{′}_{2}} =\frac{R_{2}}{𝑍^{′}_{2}}=\frac{R_{2}}{\sqrt{{𝑅_{2} }^{2}+(SX_{2})^{2}}}}… (8)$$
數值例題 1
一臺三相 50 Hz 感應電機有 8 個磁極，在某負載下以 4% 的滑差執行。確定轉子電流的頻率。
解答
$$\mathrm{轉子電流頻率，𝑓_{𝑟} = 𝑠\:𝑓 = 0.04 × 50 = 2\:Hz}$$
數值例題 2
一臺三相四極感應電機連線到 50 Hz 電源。當轉子靜止時，轉子導條中感應的電壓為 5 V。計算 500 RPM 時轉子導條中感應的電壓和頻率。
解答
$$\mathrm{同步速度，𝑁_{𝑆} =\frac{120\:𝑓}{𝑃}=\frac{120 × 50}{4}= 1500\:RPM}$$
$$\mathrm{滑差，𝑠 =\frac{𝑁_{𝑆} − 𝑁_{𝑟}}{𝑁_{𝑆}}=\frac{1500 − 500}{1500}= 0.67}$$
因此，對應於滑差 's'，
$$\mathrm{轉子感應電壓，𝑉^{′}_{2} = 𝑠\:𝑉_{2} = 0.67 × 5 = 3.35\:V}$$
$$\mathrm{轉子頻率，𝑓_{𝑟} = 𝑠\:𝑓 = 0.67 × 50 = 33.5\:Hz}$$
數值例題 3
一臺 8 極、三相、50 Hz 感應電機在滿載下以 5% 的滑差執行。轉子採用星形連線，其每相電阻和靜止電抗分別為 0.35 Ω 和 2 Ω。滑環之間的電動勢為 150 V。確定每相轉子電流和轉子功率因數。假設滑環短路。
解答
靜止狀態下每相轉子電動勢為：
$$\mathrm{𝐸_{2} =\frac{150}{\sqrt{3}}= 86.61\:V}$$
$$\mathrm{滿載時轉子每相電動勢，𝐸^{′}_{2} = 𝑠\:𝐸_{2} = 0.05 × 86.61 = 4.33\:V}$$
$$\mathrm{滿載時轉子每相電抗， 𝑋^{′}_{2} = 𝑠\:𝑋_{2} = 0.05 × 2 = 0.1\:Ω}$$
$$\mathrm{滿載時轉子每相阻抗， 𝑍^{′}_{2}=\sqrt{{0.35}^{2} + {0.1}^{2}}= 0.364\:Ω}$$
因此：
$$\mathrm{轉子每相電流 =\frac{𝐸^{′}_{2}}{𝑍^{′}_{2}}=\frac{4.33}{0.364}= 11.895\:A}$$
$$\mathrm{轉子功率因數 =\frac{𝑅_{2}}{𝑍^{′}_{2}}=\frac{0.35}{0.364}= 0.96\:(滯後)}$$
16K+ 次瀏覽
