振盪電路

---

---

振盪電路是電路所有部件的完整集合，有助於產生振盪。正如之前討論的那樣，這些振盪應該持續並且是不衰減的。讓我們嘗試分析一個實際的振盪電路，以更好地理解振盪電路的工作原理。

實際振盪電路

實際振盪電路由諧振電路、電晶體放大器和反饋電路組成。下面的電路圖顯示了實際振盪器的佈置。

現在讓我們討論這個實際振盪電路的各個部分。

• 諧振電路 - 諧振電路由一個電感 L 與電容 C 並聯組成。這兩個元件的值決定了振盪電路的頻率，因此這被稱為頻率確定電路。

• 電晶體放大器 - 諧振電路的輸出連線到放大器電路，以便在此放大諧振電路產生的振盪。因此，這些振盪的輸出由放大器增加。

• 反饋電路 - 反饋電路的功能是將一部分輸出能量以正確的相位傳輸到 LC 電路。在振盪器中，這種反饋是正反饋，而在放大器中是負反饋。

振盪器的頻率穩定性

振盪器的頻率穩定性是衡量其在較長時間間隔內保持恆定頻率的能力的指標。在較長時間內執行時，振盪器頻率可能會因增加或減少而偏離先前設定的值。

振盪器頻率的變化可能由以下因素引起：

• 所使用的有源器件（如BJT或FET）的工作點應位於放大器的線性區域。它的偏差會影響振盪器頻率。

• 電路元件效能的溫度依賴性會影響振盪器頻率。

• 施加到有源器件的直流電源電壓的變化會改變振盪器頻率。如果使用穩壓電源，則可以避免這種情況。

• 輸出負載的變化可能會導致諧振電路的Q因子發生變化，從而導致振盪器輸出頻率發生變化。

• 互電容和雜散電容的存在會影響振盪器輸出頻率，從而影響頻率穩定性。

巴克豪森準則

根據我們目前的知識，我們瞭解到實際振盪電路由諧振電路、電晶體放大器電路和反饋電路組成。因此，讓我們現在嘗試回顧一下反饋放大器的概念，以推匯出反饋放大器的增益。

反饋放大器的原理

反饋放大器通常由兩部分組成。它們是放大器和反饋電路。反饋電路通常由電阻器組成。反饋放大器的概念可以從下面的圖中理解。

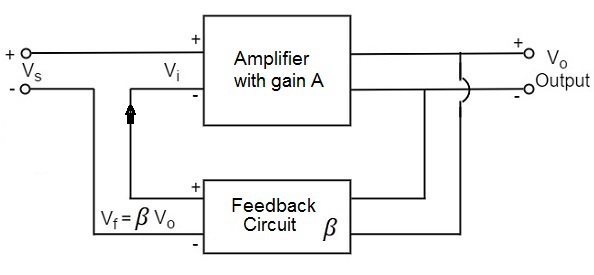
從上圖可以看出，放大器的增益表示為 A。放大器的增益是輸出電壓 Vo 與輸入電壓 V_i 的比值。反饋網路從放大器的輸出 V_o 中提取電壓 V_f = β V_o。

此電壓對於正反饋而言是相加的，對於負反饋而言是相減的，從訊號電壓 V_s 中減去。

因此，對於正反饋，

V_i = V_s + V_f = V_s + β V_o

量 β = V_f/V_o 稱為反饋比或反饋分數。

輸出 V_o 必須等於輸入電壓 (V_s + βV_o) 乘以放大器的增益 A。

因此，

$$(V_s + \beta V_o)A = V_o$$

或者

$$AV_s + A\beta V_o = V_o$$

或者

$$AV_s = V_o(1 - A\beta)$$

所以

$$\frac{V_o}{V_s} = \frac{A}{1 - A\beta}$$

設 A_f 為放大器的總增益（帶反饋的增益）。這定義為輸出電壓 V_o 與施加的訊號電壓 V_s 的比值，即

$$A_f = \frac{輸出電壓}{輸入訊號電壓} = \frac{V_o}{V_s}$$

從以上兩個方程，我們可以理解到，帶正反饋的反饋放大器增益方程由下式給出

$$A_f = \frac{A}{1 - A\beta}$$

其中 Aβ 是反饋因子或環路增益。

如果 Aβ = 1，A_f = ∞。因此增益變為無窮大，即沒有任何輸入就有輸出。換句話說，放大器充當振盪器。

條件 Aβ = 1 稱為巴克豪森振盪準則。在振盪器的概念中，這始終是一個非常重要的因素。