晶體振盪器

---

---

當振盪器處於連續工作狀態時，其頻率穩定性會受到影響。其頻率會發生變化。影響振盪器頻率的主要因素有

• 電源電壓變化
• 溫度變化
• 負載或輸出電阻的變化

在 RC 和 LC 振盪器中，電阻、電容和電感的數值會隨溫度變化而變化，因此頻率也會受到影響。為了避免這個問題，在振盪器中使用了壓電晶體。

在並聯諧振電路中使用壓電晶體可以提供振盪器的高頻率穩定性。這種振盪器稱為晶體振盪器。

晶體振盪器

晶體振盪器的原理取決於壓電效應。晶體的自然形狀是六邊形。當晶片垂直於 X 軸切割時，稱為 X 切割；當沿 Y 軸切割時，稱為 Y 切割。

晶體振盪器中使用的晶體表現出一種稱為壓電特性的特性。因此，讓我們瞭解一下壓電效應。

壓電效應

晶體表現出這樣的特性：當在晶體的一個面上施加機械應力時，在晶體的相對面上會產生電位差。反之，當在晶體的一個面上施加電位差時，在其他面上會產生機械應力。這被稱為壓電效應。

某些晶體材料，如羅謝爾鹽、石英和電氣石，表現出壓電效應，這些材料稱為壓電晶體。石英是最常用的壓電晶體，因為它價格低廉，並且在自然界中很容易獲得。

當壓電晶體受到適當的交流電位作用時，它會機械振動。當交流電壓的頻率等於晶體的固有頻率時，機械振動的幅度達到最大。

石英晶體的運作

為了使晶體在電子電路中工作，晶體被放置在兩個金屬板之間，形成電容器。石英是使用最廣泛的晶體型別，因為它價格低廉且性質穩定，同時易於獲取。交流電壓並聯施加到晶體上。

石英晶體的電路佈置如下所示：

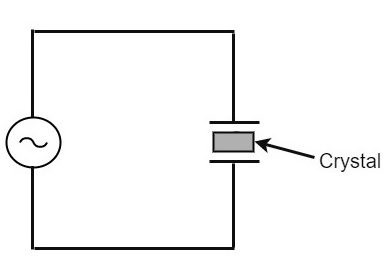
如果施加交流電壓，晶體將以施加電壓的頻率開始振動。但是，如果使施加電壓的頻率等於晶體的固有頻率，則會發生共振，晶體振動達到最大值。這個固有頻率幾乎是恆定的。

晶體的等效電路

如果我們嘗試用等效電路表示晶體，我們必須考慮兩種情況，即晶體振動和不振動。下圖分別表示晶體的符號和電等效電路。

上述等效電路由一個串聯 R-L-C 電路與電容 C_m 並聯組成。當安裝在交流電源兩端的晶體不振動時，它等效於電容 C_m。當晶體振動時，它表現得像一個調諧 R-L-C 電路。

頻率響應

晶體的頻率響應如下圖所示。該圖顯示了電抗 (X_L 或 X_C) 與頻率 (f) 的關係。很明顯，晶體有兩個緊密間隔的諧振頻率。

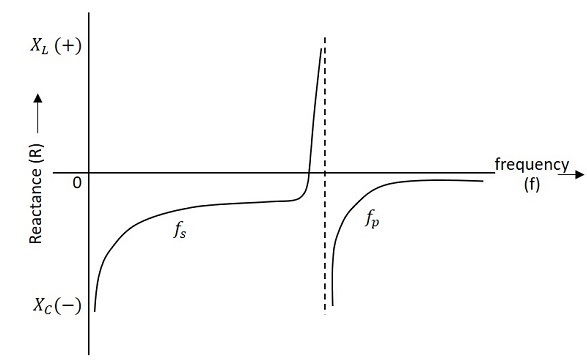
第一個是串聯諧振頻率 (f_s)，當電感的電抗 (L) 等於電容 C 的電抗時發生。在這種情況下，等效電路的阻抗等於電阻 R，振盪頻率由以下關係給出：

$$f = \frac{1}{2\pi \sqrt{L.C}}$$

第二個是並聯諧振頻率 (f_p)，當 R-L-C 支路的電抗等於電容 C_m 的電抗時發生。在此頻率下，晶體對外部電路提供非常高的阻抗，振盪頻率由以下關係給出。

$$f_p = \frac{1}{2\pi \sqrt{L.C_T}}$$

其中

$$C_T = \frac{C C_m}{(C + C_m)}$$

C_m 的值通常比 C 大得多。因此，C_T 的值近似等於 C，因此串聯諧振頻率近似等於並聯諧振頻率 (即 f_s = f_p)。

晶體振盪器電路

晶體振盪器電路可以透過多種方式構建，例如晶體控制的調諧集電極振盪器、柯爾皮茲晶體振盪器、克拉普晶體振盪器等。但是電晶體皮爾斯晶體振盪器是最常用的。此電路通常稱為晶體振盪器電路。

下面的電路圖顯示了電晶體皮爾斯晶體振盪器的佈置。

在此電路中，晶體作為反饋路徑（從集電極到基極）中的串聯元件連線。電阻 R₁、R₂ 和 R_E 提供一個分壓穩定的直流偏置電路。電容 C_E 提供發射極電阻的交流旁路，RFC（射頻扼流圈）線圈提供直流偏置，同時將電源線上任何交流訊號與輸出訊號解耦。耦合電容 C 在電路工作頻率下的阻抗可以忽略不計。但它阻擋了集電極和基極之間的任何直流電。

振盪電路頻率由晶體的串聯諧振頻率決定，其值由以下關係給出：

$$f_o = \frac{1}{2\pi \sqrt{L.C}}$$

需要注意的是，電源電壓、電晶體器件引數等的改變對電路工作頻率沒有影響，該頻率由晶體穩定。

優點

晶體振盪器的優點如下：

• 它們具有高頻穩定性。
• 晶體的品質因數 (Q) 非常高。

缺點

晶體振盪器的缺點如下：

• 它們易碎，只能用於低功率電路。
• 振盪頻率不能明顯改變。

振盪器的頻率穩定性

期望振盪器在較長時間內保持其頻率不變，以確保電路操作能夠獲得更平滑、清晰的正弦波輸出。因此，當涉及到振盪器（無論是正弦波還是非正弦波）時，頻率穩定性這個術語非常重要。

振盪器的頻率穩定性定義為振盪器在儘可能長的的時間間隔內保持所需頻率恆定的能力。讓我們嘗試討論影響此頻率穩定性的因素。

工作點的變化

我們已經瞭解了電晶體引數，並瞭解了工作點的重要性。電路中用於放大（BJT 或 FET）的電晶體的工作點穩定性至關重要。

所用有源器件的工作點被調整到其特性的線性部分。由於溫度變化，該點會發生偏移，因此穩定性會受到影響。

溫度變化

振盪器電路中的諧振電路包含各種頻率確定元件，例如電阻、電容和電感器。它們的所有引數都與溫度有關。由於溫度變化，其值會受到影響。這會導致振盪器電路頻率的變化。

由於電源

電源的變化也會影響頻率。電源變化會導致 V_cc 的變化。這將影響產生的振盪頻率。

為了避免這種情況，採用了穩壓電源系統。簡稱為 RPS。穩壓電源的詳細資訊在電子電路教程的電源部分進行了詳細討論。

輸出負載的變化

輸出電阻或輸出負載的變化也會影響振盪器的頻率。當連線負載時，諧振電路的有效電阻會發生變化。結果，LC 調諧電路的品質因數發生變化。這導致振盪器輸出頻率發生變化。

互電容的變化

互電容是在 PN 結材料（如二極體和電晶體）中產生的電容。這些電容是由於它們在工作期間存在的電荷而產生的。

互電容由於溫度、電壓等各種原因而發生變化。這個問題可以透過在有問題的互電容上並聯連線旁路電容來解決。

Q 值

振盪器中的 Q 值（品質因數）必須很高。調諧振盪器中的 Q 值決定了選擇性。由於此 Q 值與調諧電路的頻率穩定性成正比，因此應保持 Q 值較高。

頻率穩定性可以用數學方式表示為：

$$S_w = d\theta/dw$$

其中 dθ 是在標稱頻率 f_r 的小頻率變化下引入的相移。產生較大 (dθ/dw) 值的電路具有更穩定的振盪頻率。