回轉半徑

---

簡介

物體的回轉半徑通常定義為圍繞其旋轉軸的徑向距離。這個距離與一個點的轉動慣量相關聯。如果將物體的總質量集中在該點，則該轉動慣量將等於該特定物體的實際質量分佈。

回轉半徑在日常生活中各個學科中都很有用，尤其是在工程領域。在現實生活中，它用於研究柱的剛度。回轉半徑也稱為迴旋半徑。

回轉半徑是什麼意思？

物體的回轉半徑通常表示特定物體繞其特定軸的轉動慣量。但是，它可以被定義為不同的概念，因此需要注意的是，回轉半徑可以被認為是物體形心（Shaheen 等人，2018）的一個假設距離。

這個形心與橫截面積相關聯，該面積被認為集中在一個特定點，以獲得相同的轉動慣量。回轉半徑通常用 k 表示。

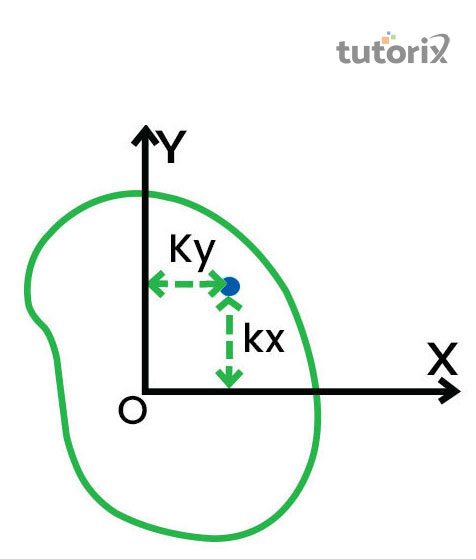
圖 1：回轉半徑

回轉半徑的數學描述是什麼？

在數學上，可以注意到回轉半徑與特定物體各部分的均方根距離相關聯。它可以是從特定軸的質心，取決於數學應用的相關性（Khatiwada，2020）。需要注意的是，它是質量點到旋轉軸的垂直距離（Haydukivska 等人，2020）。

個人可以將運動點的軌跡表示為一個物體。在這種情況下，回轉半徑可以用來定義這個被表示為物體的特定點所行進的典型距離。

回轉半徑的公式是什麼？

用回轉半徑表示轉動慣量的公式如下所示

I = mk² ……… (公式 1)

在這種情況下，I 是特定物體的轉動慣量，m 與物體的質量相關聯

因此，根據此方法，回轉半徑表示如下。

K = √I/m …….. (公式 2)

回轉半徑的單位是毫米。正如 Alsaker 等人（2019）所述，透過獲得回轉半徑，個人可以找到剛體的轉動慣量。為了更好地理解，對部分公式進行了演示。

如果一個物體有 n 個質量為 m 的粒子，則旋轉軸前的垂直距離用 r₁、r₂、r₃… r_n 表示。現在我們知道，回轉半徑的轉動慣量可以從公式 1 中得到。在那裡，透過替換，我們可以得到，

I = m₁r₁² +  m₂r₂²+ m₃r₃³…… +  m_nr_n².......... (公式 3)

如果所有粒子的質量都相同，則

I  =  { mn(r₁² + r₂²+ r₃³ + ........+ r_n² ) }/n

我們可以進一步將 mn 寫成“M”

從那裡我們可以得到，

MK² = M { (r₁² + r₂²  + r₃³ +................ + r_n²)/n }

或 K = √ (r₁² + r₂²+ r₃³  +........................+  r_n²)/n

因此，可以得出結論，回轉半徑也可以表示為特定物體相對於其特定“旋轉軸”的多個粒子的均方根距離。

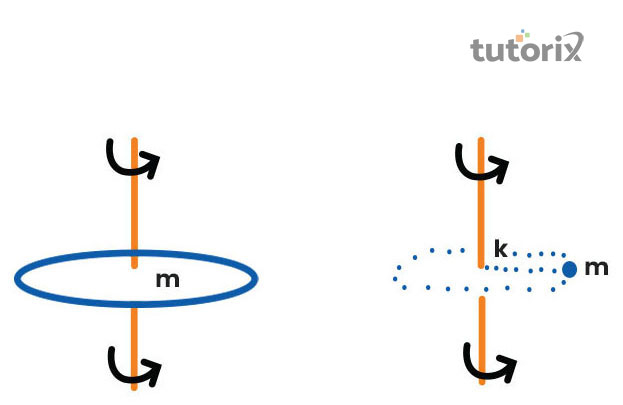
圖 2：回轉半徑

回轉半徑在現實生活中的應用是什麼？

回轉半徑可用於比較不同形狀的幾種結構在沿特定軸線受壓時的行為。這可用於預測壓縮梁的膨脹過程

回轉半徑的概念也用於地理資料分析。根據 Gurnev 等人（2020）的說法，它用於計算各種統計資料，包括各種地理位置的分佈。它也用於聚合物物理學，用於定義聚合物鏈的尺寸。

結論

回轉半徑在結構分析的各個分支中都有多種實際應用。回轉半徑的概念有助於確定物體的旋轉軸周圍的轉動慣量，該轉動慣量等於物體的實際質量分佈。它與某一點的徑向距離相關聯。但是，需要滿足某些條件，即如果物體的總質量集中在該區域，則轉動慣量可以與物體的實際質量分佈相同。

常見問題

Q1. 回轉半徑的重要性是什麼？

回轉半徑可用於確定梁或壓力的堆積情況。此外，它在橫截面積之間的強度分配中也很重要。迴旋半徑的較小估計值反映了截面處的旋轉軸，在初步研究中很重要。

Q2. 回轉半徑在結構中的用途是什麼？

回轉半徑估計了柱的剛度，如果二維回轉半徑的主慣性矩不相等，則柱將傾向於圍繞與其較小的主慣性矩相關的特定軸發生屈曲。

Q3. 影響迴旋半徑的因素有哪些？

元件的某些部分會影響回轉半徑的估計。這些因素包括特定物體的尺寸和狀態。旋轉軸的佈置和物體的位置以及其他因素取決於與物體旋轉軸相關的質量分配。

Q4. 回轉半徑的 SI 單位是什麼？

回轉半徑的 SI 單位可以用毫米或釐米或英寸來定義。它與慣性矩除以物體面積的平方根相關聯。

Q5. 迴轉的公式是什麼？

k = √IM (1) (1) k = I M 是迴轉的公式，其中回轉半徑繞旋轉軸的測量利用質量慣性矩。

參考文獻

期刊

Alsaker, C., Breidt, F. J., & van der Woerd, M. J. (2019)。小角 X 射線散射實驗中回轉半徑的最小均方誤差估計。美國統計協會雜誌，114(525)，39-47。檢索自：https://www.tandfonline.com

Gurnev, P. A., Stanley, C. B., Aksoyoglu, M. A., Hong, K., Parsegian, V. A., & Bezrukov, S. M. (2017)。半稀溶液中的聚乙二醇：本體中的回轉半徑和奈米孔中的分配。大分子，50(6)，2477-2483。檢索自：https://www.ncbi.nlm.nih.gov

Haydukivska, K., Blavatska, V., & Paturej, J. (2020)。具有複雜結構的高斯聚合物的通用尺寸比率：回轉半徑與流體力學半徑。科學報告，10(1)，1-11。檢索自：https://www.nature.com/articles/s41598-020-70649-z

Khatiwada, P. (2020)。不規則建築物的質心和回轉半徑的確定及其在扭轉分析中的應用。國際工程技術研究雜誌，7，1-7。檢索自：https://www.researchgate.net

Shaheen, M. E., Ghazy, A. R., Kenawy, E. R., & El-Mekawy, F. (2018)。雷射散射在殼聚糖分子量、第二維裡係數和回轉半徑測定中的應用。聚合物，158，18-24。檢索自：https://www.sciencedirect.com/science/article/pii/S0032386118309716

網站

Mechcontent，2022。關於回轉半徑。檢索自：https://mechcontent.com/radius-of-gyration [檢索日期：2022年6月10日]