
計算圖
反向傳播在像Tensorflow、Torch、Theano等深度學習框架中是透過使用計算圖來實現的。更重要的是,理解計算圖上的反向傳播結合了若干不同的演算法及其變體,例如透過時間的反向傳播和具有共享權重的反向傳播。一旦所有內容都被轉換為計算圖,它們仍然是相同的演算法——僅僅是在計算圖上的反向傳播。
什麼是計算圖
計算圖被定義為一個有向圖,其中節點對應於數學運算。計算圖是表達和評估數學表示式的途徑。
例如,這裡有一個簡單的數學方程:
$$p = x+y$$
我們可以繪製上述方程的計算圖如下所示。
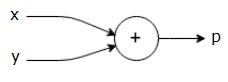
上述計算圖有一個加法節點(帶有“+”符號的節點),有兩個輸入變數x和y,以及一個輸出q。
讓我們再舉一個例子,稍微複雜一點。我們有以下方程:
$$g = \left (x+y \right ) \ast z $$
上述方程由以下計算圖表示。
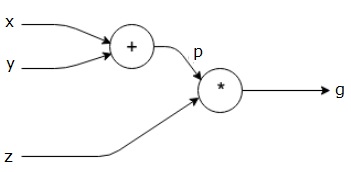
計算圖和反向傳播
計算圖和反向傳播都是深度學習中訓練神經網路的重要核心概念。
前向傳播
前向傳播是評估由計算圖表示的數學表示式值的程式。進行前向傳播意味著我們正在將值從變數向前方向從左側(輸入)傳遞到右側,輸出位於右側。
讓我們透過給所有輸入賦予一些值來舉個例子。假設所有輸入都被賦予以下值:
$$x=1, y=3, z=−3$$
透過將這些值賦予輸入,我們可以執行前向傳播並在每個節點上獲得以下輸出值。
首先,我們使用x = 1和y = 3的值,得到p = 4。
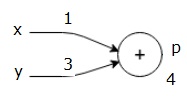
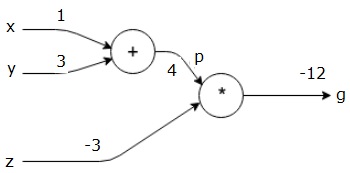
然後我們使用p = 4和z = -3得到g = -12。我們從左到右,向前進行。
反向傳播的目標
在反向傳播中,我們的目的是計算每個輸入相對於最終輸出的梯度。這些梯度對於使用梯度下降訓練神經網路至關重要。
例如,我們希望得到以下梯度:
所需梯度
$$\frac{\partial x}{\partial f}, \frac{\partial y}{\partial f}, \frac{\partial z}{\partial f}$$
反向傳播(反向傳播)
我們從找到最終輸出相對於最終輸出(自身!)的導數開始反向傳播。因此,它將產生恆等導數,其值為1。
$$\frac{\partial g}{\partial g} = 1$$
我們的計算圖現在看起來如下所示:
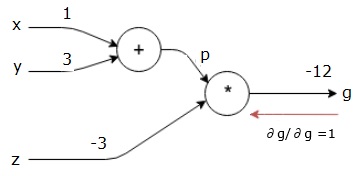
接下來,我們將透過“*”操作進行反向傳播。我們將計算p和z處的梯度。由於g = p*z,我們知道:
$$\frac{\partial g}{\partial z} = p$$
$$\frac{\partial g}{\partial p} = z$$
我們已經從前向傳播中知道了z和p的值。因此,我們得到:
$$\frac{\partial g}{\partial z} = p = 4$$
和
$$\frac{\partial g}{\partial p} = z = -3$$
我們想要計算x和y處的梯度:
$$\frac{\partial g}{\partial x}, \frac{\partial g}{\partial y}$$
然而,我們希望有效地做到這一點(儘管x和g在這個圖中只有兩跳遠,想象一下它們彼此之間非常遙遠)。為了有效地計算這些值,我們將使用微分的鏈式法則。根據鏈式法則,我們有:
$$\frac{\partial g}{\partial x}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial x}$$
$$\frac{\partial g}{\partial y}=\frac{\partial g}{\partial p}\ast \frac{\partial p}{\partial y}$$
但我們已經知道dg/dp = -3,dp/dx和dp/dy很容易,因為p直接依賴於x和y。我們有:
$$p=x+y\Rightarrow \frac{\partial x}{\partial p} = 1, \frac{\partial y}{\partial p} = 1$$
因此,我們得到:
$$\frac{\partial g} {\partial f} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial x} = \left ( -3 \right ).1 = -3$$
此外,對於輸入y:
$$\frac{\partial g} {\partial y} = \frac{\partial g} {\partial p}\ast \frac{\partial p} {\partial y} = \left ( -3 \right ).1 = -3$$
這樣向後計算的主要原因是,當我們需要計算x處的梯度時,我們只使用了已經計算過的值,以及dq/dx(節點輸出相對於同一節點輸入的導數)。我們使用區域性資訊來計算全域性值。
訓練神經網路的步驟
按照以下步驟訓練神經網路:
對於資料集中的資料點x,我們使用x作為輸入進行前向傳播,並計算成本c作為輸出。
我們從c開始進行反向傳播,並計算圖中所有節點的梯度。這包括表示神經網路權重的節點。
然後我們透過W = W - 學習率 * 梯度來更新權重。
我們重複此過程,直到滿足停止條件。