資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
服裝設計
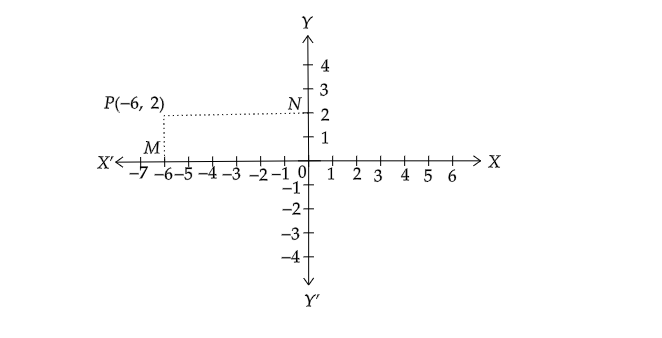
法律研究繪製點$P( -6,\ 2)$，並從該點分別作$PM$和$PN$垂直於$x$軸和$y$軸。寫出點$M$和$N$的座標。
已知：點$P( -6,\ 2)$。
要求：繪製該點。分別作$PM$和$PN$垂直於$x$軸和$y$軸。寫出點$M$和$N$的座標。
解答
i). 繪製點$P( -6,\ 2)$。
ii). 點$P( -6,\ 2)$位於第二象限。
iii). 分別作$PM$和$PN$垂直於$x$軸和$y$軸。
因為$x$軸上$y$座標始終為$0$。
因此，點$M$的座標為$( -6,\ 0)$
類似地，$y$軸上$x$座標始終為$0$。
因此，點$N$的座標為$( 0,\ 2)$。
更新於： 2022年10月10日
58 次瀏覽
廣告