資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究將一條長9釐米的線段按4:3的比例內分。並給出作圖的依據。
已知
一條長9釐米的線段。
要求
我們將一條長9釐米的線段按4:3的比例內分。
解答
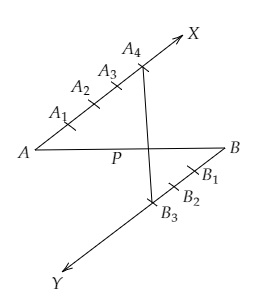
作圖步驟
(i) 作線段$AB = 9\ cm$。
(ii) 作射線$AX$，使它與$AB$成銳角。
(iii) 從$B$點作另一條射線$BY$，使它與$AX$平行。
(iv) 在$AX$上擷取4個相等的線段，在$BY$上擷取3個相等的線段。
(v) 連線$A_4$和$B_3$，交$AB$於$P$點。
$P$是所求的點，它將$AB$內分成了4:3的比例。
依據
在$\triangle \mathrm{AA}_{4} \mathrm{P}$和$\triangle \mathrm{BB}_{3} \mathrm{P}$中，
$\angle A_{4} A P=\angle P B B_{3}$ ($\angle A B Y=\angle B A X$)
$\angle \mathrm{APA}_{4}=\angle \mathrm{BPB}_{3}$ (對頂角)
因此，根據角角相似，
$\triangle \mathrm{AA}_{4} \mathrm{P} \sim \Delta \mathrm{BB}_{3} \mathrm{P}$
這意味著，
$\frac{A A_{4}}{B B_{3}}=\frac{A P}{B P}$
$\frac{A P}{B P}=\frac{4}{3}$
更新於: 2022年10月10日
42 次檢視
廣告