資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究用尺規作圖，畫出下列度數的角
(a) \( 60^{\circ} \)
(b) \( 30^{\circ} \)
(c) \( 90^{\circ} \)
(d) \( 120^{\circ} \)
(e) \( 45^{\circ} \)
(f) \( 135^{\circ} \)
要做的
我們需要畫出給定度數的角。
解答
(a)
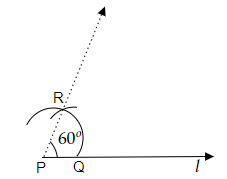
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點 $P$。
(ii) 現在，用圓規以任意半徑從點 $P$ 畫弧，並標記弧與直線 $l$ 交點為點 $R$。
(iii) 現在，用圓規保持與之前相同的半徑，從點 $R$ 在之前的弧上畫弧，並標記交點為 $S$。
(iv) 現在，讓我們連線點 $P$ 和 $S$。因此，形成了所需的與直線 $l$ 構成 $60^o$ 角。
(b)
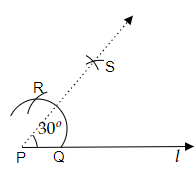
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點 $P$。現在，用圓規以任意半徑從點 $P$ 畫弧，並標記弧與直線 $l$ 交點為 $Q$。
(ii) 現在，用圓規保持與之前相同的半徑，從點 $Q$ 畫另一條弧，並標記此弧與之前弧的交點為 $R$。
(iii) 現在，用圓規以大於點 $Q$ 到點 $R$ 長度一半的半徑分別從點 $P$ 和 $Q$ 畫弧，並標記這兩條弧的交點為點 $S$。
(iv) 現在，讓我們連線點 $S$ 和點 $P$。因此，$\overline{PS}$ 與直線 $l$ 構成了所需的 $30^o$ 角。
(c)
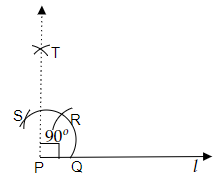
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點 $P$。現在，用圓規以任意半徑從點 $P$ 畫弧，並標記此弧與直線 $l$ 的交點為 $Q$。
(iii) 現在，用圓規保持與之前相同的半徑，從點 $Q$ 畫另一條弧，並標記此弧與之前弧的交點為點 $R$。
(iv) 現在，用圓規保持與之前相同的半徑，從點 $R$ 畫另一條弧，並標記此弧與第一條弧的交點為點 $S$。
(iv) 現在，用圓規保持與之前相同的半徑，分別從點 $R$ 和點 $S$ 畫兩條弧，並標記這兩條弧的交點為點 $T$。
(v) 現在，讓我們連線點 $P$ 和點 $T$。因此，形成了所需的與直線 $l$ 構成 $90^o$ 角。
(d)
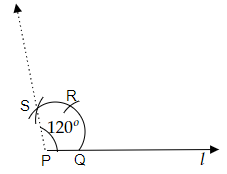
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點 $P$。現在，用圓規以任意半徑從點 $P$ 畫弧，並標記弧與直線 $l$ 的交點為點 $Q$。
(ii) 現在，用圓規保持與之前相同的半徑，從點 $Q$ 畫另一條弧，並標記此弧與之前畫的弧的交點為點 $R$。
(iii) 現在，用圓規保持與之前相同的半徑，從點 $R$ 畫另一條弧，並標記此弧與第一條弧的交點為點 $S$。
(iv) 現在，連線點 $S$ 和 $P$。因此，形成了所需的與直線 $l$ 構成 $120^o$ 角。
(e)
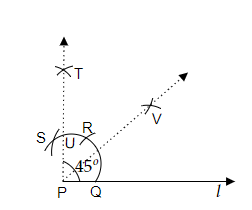
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點 $P$。
(ii) 現在，用圓規以任意半徑從點 $P$ 畫弧，並標記此弧與直線 $l$ 的交點為點 $Q$。
(iii) 現在，用圓規保持與之前相同的半徑，從點 $Q$ 畫弧，並標記此弧與之前弧的交點為點 $R$。
(iv) 現在，用圓規保持與之前相同的半徑，從點 $R$ 畫弧，並標記此弧與第一條弧的交點為點 $S$。
(v) 現在，用圓規保持與之前相同的半徑，分別從點 $R$ 和點 $S$ 畫兩條弧，並標記這兩條弧的交點為點 $T$。讓我們連線點 $T$ 和點 $P$。
(vi) $\overline{PT}$ 與第一條畫的弧相交於某一點，讓我們標記此點為點 $U$。
(vii) 現在，用圓規以大於點 $Q$ 到 $U$ 長度一半的半徑分別從點 $Q$ 和點 $U$ 畫兩條弧，並標記這兩條弧的交點為 $V$。
(viii) 現在，讓我們連線點 $P$ 和點 $V$。因此，形成了所需的與直線 $l$ 構成 $45^o$ 角。
(f)
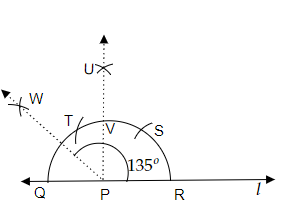
作圖步驟
(i) 讓我們畫一條任意長度的直線 $l$，並在直線 $l$ 上標記一個點。
(ii) 現在，用圓規以任意半徑從點 $P$ 畫半圓，並標記此半圓與直線 $l$ 的交點分別為點 $Q$ 和點 $R$。
(iii) 現在，用圓規保持與之前相同的半徑，從點 $R$ 畫弧，並標記此弧與之前半圓的交點為點 $S$。
(iv) 現在，用圓規保持與之前相同的半徑，從點 $S$ 畫弧，並標記此弧與半圓的交點為點 $T$。
(v) 現在，保持與之前相同的半徑，分別從點 $S$ 和點 $T$ 畫兩條弧，並標記這兩條弧的交點為點 $U$。
(vi) 現在，讓我們連線點 $P$ 和點 $U$，並標記此 $\overline{PU}$ 與半圓的交點為點 $v$。
(vii) 現在，用圓規以大於點 $Q$ 到點 $V$ 長度一半的半徑畫弧，並標記這兩條弧的交點為點 $W$。
(viii) 現在，讓我們連線點 $P$ 和點 $W$。因此，形成了所需的與直線 $l$ 構成 $135^o$ 角。
54 次瀏覽
