資料結構
網路
關係資料庫管理系統(RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法學研究多路複用器作為通用邏輯閘
閱讀本文，瞭解如何使用多路複用器實現通用邏輯閘。讓我們從簡要介紹多路複用器和通用邏輯閘開始。
什麼是多路複用器？
多路複用器或MUX或資料選擇器是一種組合邏輯電路，它接受多個數據輸入，並只允許其中一個數據在任何時候透過輸出通道。多路複用器的框圖如圖1所示。
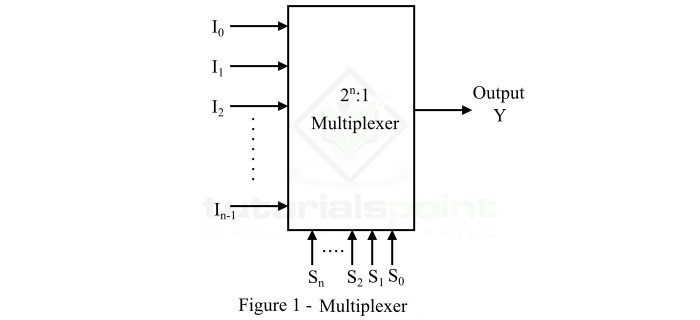
多路複用器由2n個數據輸入線、n個選擇線和一個輸出線組成。施加到選擇線的邏輯電平決定哪個輸入將傳遞到輸出通道。
根據資料輸入線的數量，多路複用器可以有多種型別，例如2:1 MUX、4:1 MUX、8:1 MUX等。在數位電子技術中，多路複用器用於多種應用，例如實現布林函式和不同型別的邏輯閘。
什麼是通用門？
通用邏輯閘是一種邏輯閘（用於執行邏輯運算的數字裝置），它可以用來實現任何型別的邏輯功能或其他基本邏輯閘，例如OR、AND、NOT等。
在數位電子技術中，我們有兩種通用邏輯閘，即與非門和或非門。
與非門
與非門是一種通用邏輯閘。與非門基本上是兩個基本邏輯閘的組合，即AND門和非門，即
NAND Logic = AND Logic + NOT Logic
與非門的輸出在所有輸入都為高電平時為低電平，而在任何輸入為低電平時為高電平。因此，與非門的操作與與門的操作相反。一個雙輸入與非門的邏輯符號如圖2所示。
對於與非門，如果A和B是輸入變數，Y是輸出變數，則其輸出方程由下式給出：
$$Y=\overline{A\cdot B}=\left ( A\cdot B \right )'$$
它讀作“Y等於A·B的全反”。
可以透過下表給出的真值表來分析與非門在不同輸入組合下的操作。
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y = (A.B)' |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
或非門
或非門是另一種通用邏輯閘。這裡，或非門意味著非+或。這意味著，或門的輸出被非或反轉。因此，或非門是或門和非門的組合，即
NOR Gate = OR Gate + NOT Gate
或非門是一種邏輯閘，只有當所有輸入都為低電平時，其輸出才為高電平；即使任何輸入變為高電平，它也會輸出低電平。一個雙輸入或非門的邏輯符號如圖3所示。
對於或非門，如果A和B是輸入變數，Y是輸出變數，則或非門的輸出方程由下式給出：
$$Y=\overline{A + B}=\left ( A + B \right )'$$
它讀作“Y等於A加B的全反”。
我們可以透過下表給出的真值表來分析或非門在不同輸入組合下的操作。
| 輸入 | 輸出 | |
|---|---|---|
| A | B | Y = (A+B)' |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
現在，在簡要介紹了多路複用器、與非門和或非門之後，我們可以討論使用多路複用器實現這些通用邏輯閘的方法。
使用多路複用器實現與非門
圖4顯示了使用多路複用器實現雙輸入與非門的方法。
由於雙輸入與非門共有四(22 = 4)種可能的輸入變數組合。因此，要實現雙輸入與非門，我們需要一個4:1 MUX。
根據雙輸入與非門的真值表，對於前三種組合（即00、01、10），輸出Y = 1。因此，多路複用器的輸入線I0、I1和I2連線到邏輯1。對於組合11，與非門的輸出Y = 0，因此MUX的輸入線I3連線到邏輯0。
透過這種方式，我們可以使用多路複用器實現與非門。現在，讓我們討論使用多路複用器實現或非門的方法。
使用多路複用器實現或非門
圖5顯示了使用多路複用器實現雙輸入或非門的方法。
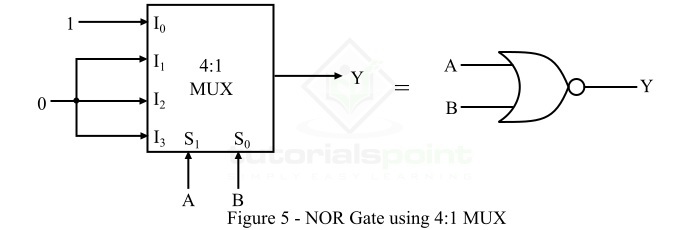
由於雙輸入或非門共有四(22 = 4)種可能的輸入變數組合。因此，要實現雙輸入或非門，我們需要一個4:1 MUX。
或非門的輸入變數A和B用作多路複用器的選擇線。其中，A和B分別應用於S1和S0。
根據雙輸入或非門的真值表，只有在輸入變數的第一種組合（即00）時，輸出Y = 1。因此，我們只將邏輯1應用於多路複用器的輸入資料線I0。對於所有其他組合（即01、10和11），或非門的輸出Y = 0，因此MUX的輸入線I1、I2和I3連線到邏輯0。這樣，就可以使用多路複用器實現或非門。
練習題
嘗試解決以下練習題，以精通使用多路複用器實現通用邏輯閘。
問1 - 使用8:1 MUX實現三輸入與非門。
問2 - 使用8:1 MUX實現三變數或非門。
3K+ 瀏覽量
