麥克斯韋方程組

---

簡介

如果你在電動力學概念方面花了一些時間，那麼你很有可能已經以某種形式接觸過麥克斯韋方程組。即使當時你不知道它們叫什麼，它們也一定會在你的概念中出現過。

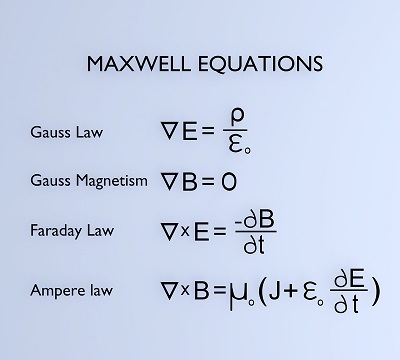
麥克斯韋方程組構成了電動力學的基石。這四個方程與洛倫茲力定律一起構成了電動力學的基礎，並且每個問題都可以單獨使用這五個方程來解決。在本教程中，我們將討論位移電流和麥克斯韋方程組。

什麼是位移電流？

你一定學習過高斯定律、安培定律、法拉第定律等。你一定也學習過磁通密度的散度$\mathrm{\overrightarrow{B}}$是一個消失的量。也就是說$\mathrm{\overrightarrow{\nabla}.\overrightarrow{B}\:=\:0}$ 這些方程對於靜態情況來說是很好用的。但是，當電流不是隨時間恆定不變時，安培定律就開始失效了。

為了糾正安培定律中的問題，麥克斯韋提出了新增一個稱為位移電流密度的項，表示為位移場$\mathrm{\overrightarrow{D}}$的時間導數。從物理上講，位移電流密度表示隨時間變化的電場對安培定律的貢獻。

請注意，位移電流密度本身並不是真正的電流。相反，它是電位移場的時間導數。在數學上，

$$\mathrm{\overrightarrow{D}\:=\:\varepsilon_{0}\overrightarrow{E}\:+\:\overrightarrow{P}}$$

這裡，𝜖0是自由空間的介電常數，$\mathrm{\overrightarrow{E}}$是外加電場，$\mathrm{\overrightarrow{P}}$是極化強度。在這種情況下，

$$\mathrm{位移電流密度\:=\:\frac{\partial\overrightarrow{D}}{\partial\:t}}$$

麥克斯韋第一方程

雖然討論麥克斯韋方程組沒有特定的順序，但由於其簡單性，人們可以認為高斯定律是第一個。

根據高斯定律，從一個表面流出的電場量與封閉在其內部的電荷成正比。請注意，在這種情況下，我們談論的是靜態電場。在討論高斯定律時，表面的選擇是完全任意的，我們選擇最方便的那個。

在數學上，

$$\mathrm{\overrightarrow{\nabla}.\overrightarrow{E}\:=\:\frac{Q}{\varepsilon_{0}}}$$

𝑄表示我們選擇的表面內封閉的總電荷。

麥克斯韋第二方程

對於第二個方程，我們將注意力轉向通常稱為磁高斯定律的關係，儘管它並非真正的高斯定律。這種關係普遍成立，沒有違反它的情況。

第二個方程意味著磁通密度的散度消失。在數學上，

$$\mathrm{\overrightarrow{\nabla}.\overrightarrow{B}\:=\:0}$$

這個方程的物理意義是磁單極子不存在。因此，你可以擁有獨立存在的正電荷和負電荷。但是，你不可能以某種方式存在北極和南極彼此獨立的情況。即使你將一根條形磁鐵切成兩半，它也會導致兩對南極和北極，而不是一個孤立的北極和一個孤立的南極。

麥克斯韋第三方程

第三個方程背後的概念非常有趣，它表明變化的磁場會產生電場。因此，這種關係是建立電和磁之間聯絡的一個關係。

這個概念是由法拉第提出的，也稱為法拉第電磁感應定律。它寫成如下：

$$\mathrm{\overrightarrow{\nabla}.\overrightarrow{E}\:=\:-\:\frac{\partial\overrightarrow{B}}{\partial\:t}}$$

負號表示相反的方向。這是法拉第電磁感應定律用微分形式和電場和磁場表示。你一定以另一種形式學習過它，

$$\mathrm{\varepsilon\:=\:-\:\frac{\;d\phi}{dt}}$$

這裡，𝜖是感應電動勢，而𝜙是穿過線圈面積的磁通量。

麥克斯韋第四方程

第四個麥克斯韋方程是電動力學歷史上最優雅和最具突破性的發現。第三個方程建立了電和磁之間的關係，而這個方程加強了這種聯絡，並使其成為雙向的，而不是單向的。

根據這個方程，變化的電場會產生磁場，就像變化的磁場會產生電場一樣。

最初，這是安培定律，它只將磁通密度與封閉電流聯絡起來。然而，麥克斯韋發現，在動態情況下，它會失效，因此透過新增一個額外的項來“修復”它。現在，第四個麥克斯韋方程被稱為安培-麥克斯韋定律，寫成如下：

$$\mathrm{\overrightarrow{\nabla}\times\overrightarrow{B}\:=\:\mu_{0}(\overrightarrow{J}\:+\:\varepsilon_{0}\frac{\partial\overrightarrow{E}}{\partial\:t})}$$

𝐽→是電流密度。

麥克斯韋方程組的意義

麥克斯韋方程組是電動力學中極其重要和基本的定律，其中包含了我們對電動力學的全部知識。你必須知道，真空中光速是一個普遍的和基本的常數。透過結合麥克斯韋方程組並將它們與一般的波動方程進行比較，可以證明電磁波以該速度傳播。

麥克斯韋方程組也以各種形式用於解決邊值問題和相當容易地分析不同的場景。這些方程也與量子力學和愛因斯坦的廣義相對論很好地配合。

結論

位移電流密度表示隨時間變化的電場對磁通密度的貢獻，並出現在麥克斯韋方程組中，以補償安培環路定律中遇到的問題。它僅在變化的電場情況下才有意義，並且當電場隨時間恆定時消失。如果$\mathrm{\overrightarrow{D}}$表示電位移場，則位移電流密度由$\mathrm{\frac{\partial\overrightarrow{D}}{\partial\:t}}$給出。

麥克斯韋方程組構成了電動力學的基石，並且與洛倫茲力定律一起可以完全解釋其中包含的概念。這些方程對於理解電動力學概念極其重要，並且也可以很容易地調整為靜態情況。

常見問題

1. 位移電流與位移電流密度是否不同？

命名法相當混亂。位移電流本身並不代表電動力學中使用的物理量。相反，我們要麼處理電位移向量$\mathrm{\overrightarrow{D}}$，要麼處理其時間導數，即位移電流密度。

2. 如果磁單極子存在，麥克斯韋第二方程會發生什麼？

在這種（迄今尚未實現的）情況下，磁通密度的散度將不為零。其符號將取決於所討論的具體情況。

3. 我們如何證明電磁波以光速傳播？

這是透過用標量勢和向量勢表示麥克斯韋方程組來實現的。我們實質上得到了電場和磁場的非齊次波動方程，這給了我們波速的值。

4. 我見過麥克斯韋方程組的積分形式。它們正確嗎？

是的。麥克斯韋方程組可以用微分形式和積分形式表示。透過應用數學物理的概念，從一種形式轉換為另一種形式非常容易。

Q5. 位移電流密度這個名稱從何而來？

麥克斯韋對安培定律的修正包括新增項$\mathrm{\mu_{0}\epsilon_{0}\:=\:\frac{\partial\overrightarrow{E}}{\partial\:t}}$。這可以與電位移向量$\mathrm{\overrightarrow{D}}$相關聯，因為$\mathrm{\overrightarrow{D}\:=\:\varepsilon_{0}\overrightarrow{E}\:+\:\overrightarrow{P}}$