資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝學
法學C++中直角等腰三角形內最多能容納多少個正方形
任務是找到在一個給定底邊為‘s’的直角等腰三角形內最多能容納多少個邊長為‘a’的正方形（等腰三角形至少有兩條邊相等）。
讓我們用一個例子來理解我們要做什麼
輸入
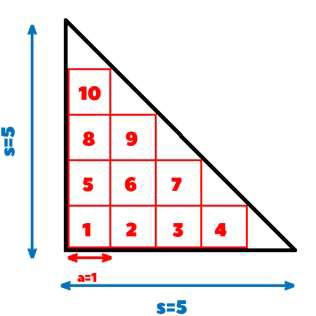
s=5, a=1
輸出
10
解釋 − 底部正方形的數量可以透過將s除以a並減去1來計算。所以底部正方形的數量 = 5/1 – 1 = 4。
類似地，當放置底部4個正方形時，我們得到一個新的等腰三角形，底邊為(s-a)，然後我們重複相同的步驟，得到3個正方形，依此類推，直到頂部放置一個正方形。
輸入
s=7, a=2
輸出
3
下面程式中使用的演算法如下
為了找到最大正方形數量，我們必須從三角形的底邊開始，計算正方形的數量。
要找到正方形的數量，我們將底邊s除以正方形的邊長a，然後從中減去1 = s/a – 1。
然後它會留下另一個底邊為(s - a)的等腰三角形，它容納的正方形數量比其下方前一行少一個，我們可以用以下方式計算：
下一行的正方形數量 = (s - a)/a – 1 = (s/a – a/a) – 1= s/a - 1 - 1 = s/a – 2 = 比前一行少一個正方形。
正方形的數量不斷減少，直到達到1，因此我們只需要找到底行的正方形數量，並使用求自然數之和的公式來找到最終的總和，即：
(n) * (n + 1) / 2
在這種情況下，公式變為 − ((s / a) – 1) * (s / a) / 2
示例
#include<bits/stdc++.h>
using namespace std;
int Max(int s, int a){
//formula for calculating maximum squares
return ((s / a) - 1) * (s / a) / 2;
}
//Main function
int main(){
int s = 5, a = 1;
cout <<"Maximum squares possible are: "<<Max(s,a);
return 0;
}輸出
10
更新於：2020年8月3日
瀏覽量 299
廣告