資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究線性迴歸
從給定的一組資料點中，線性迴歸找到一條直線的方程。給定的點將遵循直線。使用此公式，我們可以預測當前不在集合中的其他特定點的值。
要使用一些資料點解決線性迴歸問題，我們必須遵循以下公式
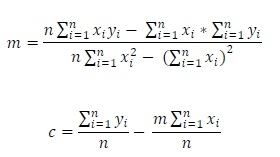
這裡的 m 和 c 分別是斜率和 y 截距。使用這些表示式，我們可以在此形式下得到直線方程：𝑦 = 𝑚𝑥 + 𝑐。
輸入和輸出
Input:
The (x, y) coordinates of some points. {(1,3), (2,4), (3,5), (4,6), (5,8)}
Output:
The slope: 1.2 The Intercept: 1.6
The equation: y = 1.2x + 1.6演算法
linReg(coord)
輸入：給定的座標點集合。
輸出：斜率 m 和 y 截距 c。
Begin for i := 1 to n, do sumX := sumX + coord[i,0] sumY := sumY + coord[i,1] sumXsq := sumXsq + (coord[i,0]*coord[i,0]) sumXY := sumXY + (coord[i,0] * coord[i,1]) done m := (n * sumXY – (sumX*sumY)) / (n * sumXsq – (sumX * sumX)) c := (sumY / n) – (m * sumX)/n End
示例
#include<iostream>
#include<cmath>
#define N 5
using namespace std;
void linReg(int coord[N][2], float &m, float &c) {
float sx2 = 0, sx = 0, sxy = 0, sy = 0;
for(int i = 0; i<N; i++) {
sx += coord[i][0]; //sum of x
sy += coord[i][1]; //sum of y
sx2 += coord[i][0]*coord[i][0]; //sum of x^2
sxy += coord[i][0]*coord[i][1]; //sum of x*y
}
// finding slope and intercept
m = (N*sxy-(sx*sy))/(N*sx2-(sx*sx));
c = (sy/N)-(m*sx)/N;
}
main() {
// this 2d array holds coordinate points
int point[N][2] = {{1,3},{2,4},{3,5},{4,6},{5,8}};
float m, c;
linReg(point, m, c);
cout << "The slope: " << m << " The Intercept: " << c << endl;
cout << "The equation: " << "y = "<< m <<"x + "<< c;
}輸出
The slope: 1.2 The Intercept: 1.6 The equation: y = 1.2x + 1.6
更新於：2020-06-17
930 瀏覽
廣告