機器學習中的多元線性迴歸

---

介紹

多元線性迴歸是關鍵的迴歸技術之一，它模擬了一個連續因變數與多個自變數之間的線性關係。

線性迴歸演算法有兩類：

簡單−僅處理兩個特徵。

多元−同時處理兩個以上特徵。

讓我們在本文中詳細研究多元線性迴歸。

多元線性迴歸

多元線性迴歸是一種常用的預測分析方法。使用這種分析方法，您可以理解一個連續因變數與兩個或多個自變數之間的關係。

自變數可以是分類變數或連續變數，例如年齡和身高（例如性別和職業）。重要的是要記住，如果給定的因變數是分類變數，則應在進行分析之前對其進行偽編碼。

公式和計算

多元迴歸分析允許同時控制影響因變數的多個因素。可以使用迴歸分析來檢查自變數和因變數之間的關係。

設k代表用字母x1、x2、x3……xk表示的變數的數量。

為了使用這種方法，我們必須假設我們有k個可以設定的自變數。然後這些變數將機率性地決定結果Y。

此外，我們假設Y直接依賴於變數，如

Y = β0 + β1x1 + β2x2 + · · · + βkxk + ε

• 它依賴於或預計變數yi

• y截距決定y的斜率，因此當xi和x2都為零時，y將為0。

• 導致y變化的xi1和xi2的一個單位變化由迴歸係數1和2表示。

• 所有自變數的斜率係數用符號p表示。

• 該短語描述了模型中的隨機誤差（殘差）。

• 除了k不等於1的要求外，這與簡單線性迴歸相同，其中是標準誤差。

我們有超過k個觀測值，n通常遠大於k。

我們測量隨機變數Yi的值yi，並將自變數分配給第i個觀測值的xi1、xi2……xik值。

因此，可以使用以下方程來描述模型。

Yi = β0 + β1xi1 + β2xi2 + · · · + βkxik + i for i = 1, 2, . . . , n

其中誤差i是具有相同未知方差2和均值為0的獨立標準變數。

線性迴歸和多元迴歸的區別

在預測複雜過程的結果時，多元線性迴歸優於簡單線性迴歸。

簡單線性迴歸可以精確地捕捉簡單關係中兩個變數之間的關係。但是，多元線性迴歸可以識別需要更深入分析的更復雜的關係。

多元迴歸模型使用多個自變數。它不受簡單迴歸方程的相同限制，因為它可以擬合曲線和非線性關係。多元線性迴歸的用途如下。

• 控制和規劃。

• 預測

估計變數之間的關係可能很有趣也很有幫助。多元迴歸模型根據解釋變數對預測因變數值的貢獻來評估變數之間的關係，就像所有其他迴歸模型一樣。

示例

import numpy as nm
import matplotlib.pyplot as pylt
import pandas as ps
dataset = ps.read_csv('https://raw.githubusercontent.com/mkgurucharan/Regression/master/Startups_Data.csv')
X1 = dataset.iloc[:, :-1].values
y = dataset.iloc[:, -1].values
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
ctlo = ColumnTransformer(transformers=[('encoder', OneHotEncoder(), [3])],
remainder='passthrough')
X1 = nm.array(ctlo.fit_transform(X1))
print(X1)
from sklearn.model_selection import train_test_split
X1_train, X1_test, y_train, y_test = train_test_split(X1, y, test_size = 0.2)
from sklearn.linear_model import LinearRegression
regressor_one = LinearRegression()
regressor_one.fit(X1_train, y_train)
y_pred = regressor.predict(X1_test)
df = ps.DataFrame({'Real Values':y_test, 'Predicted Values':y_pred})
df

輸出

Predicted Values has a value of 74963.60

MLR 圖表外觀

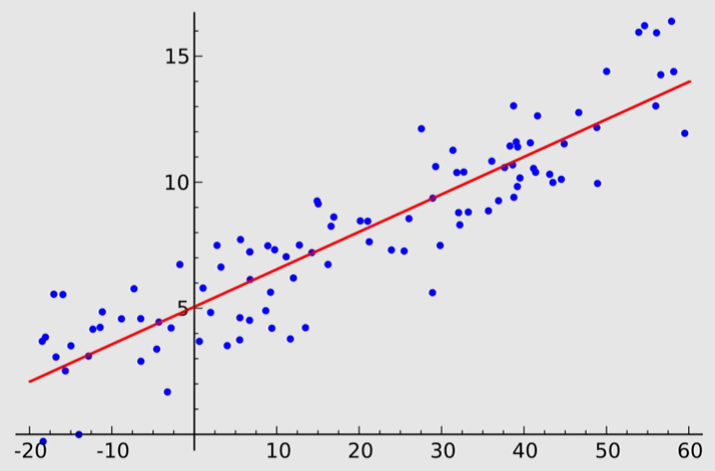
MLR 的用法

當我們想要使用多個自變數來預測因變數時，我們使用多元迴歸。它與普通最小二乘法 (OLS) 迴歸是同一種迴歸。另一方面，透過根據解釋變數值的改變來對比這些變數的分佈，OLS 迴歸確定解釋變數對連續因變數的影響。

MLR 允許同時使用多個解釋變數。因此，您可以更準確地估計如果實施特定更改，您的資料會發生什麼。

確保資料滿足以下五個要求，以確保它適合線性迴歸分析：

• 因變數和自變數之間存在直線關係

• 自變數之間沒有太大的相關性。

• 殘差的方差始終相同。

• 觀測的獨立性（即，每個觀測都應獨立收集）。

• 多元正態性（即，所有變數都應服從正態分佈）。

結論

多元線性迴歸是一種統計方法，用於模擬涉及兩個或多個自變數和一個因變數的更復雜的關係。當存在兩個或多個x變數時，使用它。