機器學習中的Python多項式迴歸

介紹

在多項式迴歸中，因變數Y和自變數X之間的關係被建模為多項式的n次方，這是一種線性迴歸。這樣做是為了使用資料點繪製最佳擬合曲線。讓我們在這篇文章中進一步探討多項式迴歸。

多項式迴歸

多項式迴歸是多元線性迴歸模型的罕見情況之一。換句話說，當因變數和自變數之間存在曲線關係時，它是一種線性迴歸。它擬合數據中的多項式關係。

此外，透過包含多個多項式項，多個線性迴歸方程被轉換成多項式迴歸方程。

在多項式迴歸中，自變數x和因變數y之間的關係被建模為n次多項式。多項式迴歸擬合自變數x的值與其條件均值y (用E(y|x)表示)之間的非線性關係。

多項式迴歸的必要性

以下是指定多項式迴歸需求的一些標準。

  • 如果像簡單線性迴歸那樣，將線性模型應用於線性資料集，則會產生良好的結果。但是，如果將此模型應用於非線性資料集而無需調整，則會計算出較差的結果。這些會導致誤差率增加，準確性下降以及損失函式的增加。

  • 當資料點以非線性方式排列時，需要多項式迴歸。

  • 如果存在非線性模型並且我們嘗試擬合線性模型，則線性模型將無法覆蓋任何資料點。為了確保覆蓋所有資料點，使用多項式模型。然而，對於大多數資料點，使用多項式模型時，曲線比直線更有效。

  • 如果我們嘗試將線性模型擬合到曲線資料，則殘差（Y軸）與預測變數（X軸）的散點圖將顯示中間區域的許多正殘差。因此，在這種情況下它是不合適的。

多項式迴歸的應用

基本上，它們用於定義或列舉非線性現象。

  • 組織生長速率。

  • 流行病的進展。

  • 湖泊沉積物中碳同位素的分佈。

迴歸分析的基本目標是根據自變數x的值對因變數y的估計值進行建模。在簡單迴歸中，我們使用以下方程

y = a + bx + e

這裡，因變數是y，自變數是a，b和e。

多項式迴歸型別

存在多種多項式迴歸，因為多項式方程的次數沒有上限，可以高達n次方。例如，多項式方程的二次方通常被稱為二次方程。如上所述，該次數有效，直到n次方，我們可以根據需要推匯出任意多個方程。因此，多項式迴歸通常分類如下。

  • 當次數為1時，為線性。

  • 方程的次數為2，為二次。

  • 三次方，次數為3，依此類推。

例如，當根據合成發生的溫度檢查化學合成的輸出時，此線性模型通常不起作用。在這種情況下，我們使用二次模型。

y = a+b1x+b2+b2+e

這裡，誤差率為e，y截距為a，y是x的因變數。

Python中的多項式迴歸實現

步驟1 - 匯入資料集和庫

匯入必要的庫以及用於多項式迴歸分析的資料集。

# Importing up the libraries
import numpy as nm
import matplotlib.pyplot as mplt
import pandas as ps
# Importing up the dataset
data = ps.read_csv('data.csv')
data

輸出

   sno Temperature Pressure
0    1     0        0.0002
1    2     20       0.0012
2    3     40       0.0060
3    4     60       0.0300
4    5     80       0.0900
5    6     100      0.2700

步驟2 - 第二步將資料集分成兩部分。

將資料集分成X和y兩部分。X將包含第1列和第2列。y列將包含這兩列。

X = data.iloc[:, 1:2].values
y = data.iloc[:, 2].values

步驟3 - 使用線性迴歸擬合數據集

擬合線性迴歸模型的兩個組成部分。

from sklearn.linear_model import LinearRegressiondata
line2 = LinearRegressiondata()
line2.fit(X, y)

步驟4 - 將多項式迴歸擬合到資料集

將多項式迴歸模型擬合到X和Y兩個組成部分。

from sklearn.preprocessing import PolynomialFeaturesdata
poly = PolynomialFeaturesdata(degree = 4)
X_polyn = polyn.fit_transform(X)
polyn.fit(X_polyn, y)
line3 = LinearRegressiondata()
line3.fit(X_polyn, y)

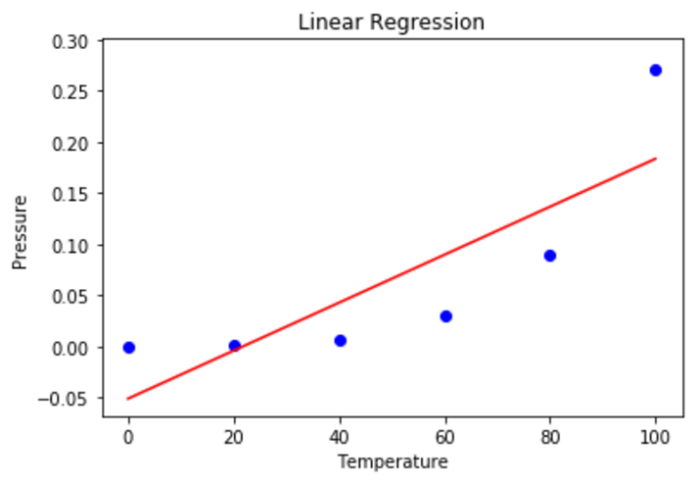
步驟5 - 在此步驟中，我們使用散點圖來視覺化線性迴歸的結果。

mplt.scatter(X, y, color = 'blue')
mplt.plot(X, lin.predict(X), color = 'red')
mplt.title('Linear Regression')
mplt.xlabel('Temperature')
mplt.ylabel('Pressure')
mplt.show()

輸出

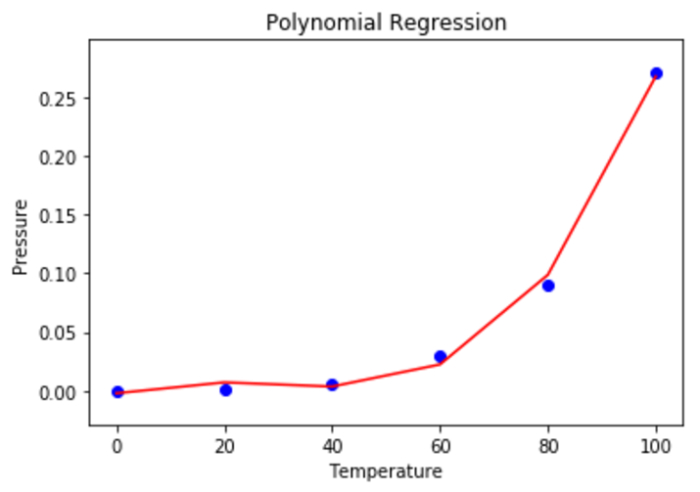
步驟6 - 使用散點圖視覺化多項式迴歸的結果。

mplt.scatter(X, y, color = 'blue')
mplt.plot(X, lin2.predict(polyn.fit_transform(X)), color = 'red')
mplt.title('Polynomial Regression')
mplt.xlabel('Temperature')
mplt.ylabel('Pressure')
mplt.show()

輸出

步驟7 - 使用線性迴歸和多項式迴歸來預測未來的結果。需要注意的是，輸入變數必須包含在一個NumPy 2D陣列中。

線性迴歸

predic = 110.0
predicdarray = nm.array([[predic]])
line2.predict(predicdarray)

輸出

Array([0.20657625])

多項式迴歸

Predic2 = 110.0
predic2array = nm.array([[predic2]])
line3.predicdict(polyn.fit_transform(predicd2array))

輸出

Array([0.43298445])

優點

  • 它能夠執行各種各樣的任務。

  • 通常，多項式適合各種曲面。

  • 多項式提供了變數之間關係的最佳近似表示。

缺點

  • 它們對異常值非常敏感。

  • 一個或兩個變數的存在可能會嚴重影響非線性分析的結果。

  • 此外，與線性迴歸相比，不幸的是，用於發現非線性迴歸中異常值的模型驗證技術較少。

結論

在本文中，我們學習了多項式迴歸背後的理論。我們學習了多項式迴歸的實現。

在將此模型應用於真實資料集後，我們可以看到它的圖形並使用它來進行預測。我們希望本節內容對您有所幫助，並且現在我們可以自信地將此知識應用於其他資料集。

更新於：2022年12月27日

940 次瀏覽

開啟您的職業生涯

透過完成課程獲得認證

開始學習
廣告