資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學為什麼在機器學習分類中使用邏輯迴歸？
介紹
邏輯迴歸是一種常用的機器學習二元分類演算法。儘管名稱中包含“迴歸”一詞，但它實際上是一種分類演算法。它使用對數機率，並以對數損失或交叉熵損失作為代價函式。
在本文中，讓我們看看為什麼邏輯迴歸本質上是一種分類演算法。
邏輯迴歸作為一種分類演算法
線性迴歸演算法可以用線性方程表示，例如，具有截距$\mathrm{\alpha_{0}}$和係數$\mathrm{\alpha_{1}}$的單變量回歸模型可以寫成：
$$\mathrm{y=\alpha_{0}+\alpha_{1}x}$$
線性迴歸的最佳擬合線如下圖所示。
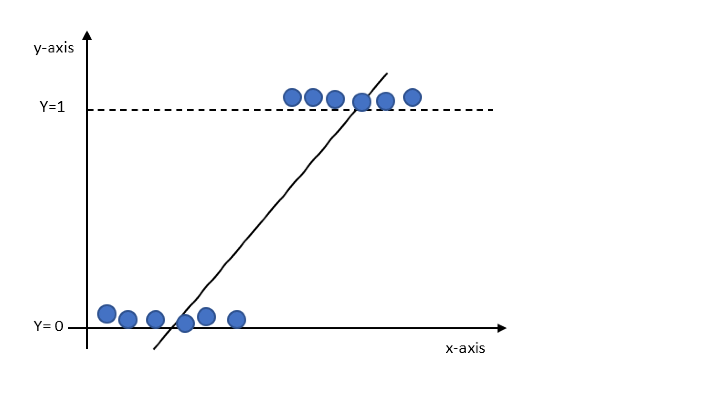
然而，在邏輯迴歸中，值只能在0和1之間，但線上性迴歸中，值是連續的，並且根據最佳擬合線可以超過0和1。
這清楚地表明，必須轉換線性迴歸方程，使其適應範圍為[0,1]的值。這是透過使用 sigmoid 函式實現的，尤其是在邏輯迴歸中，它將值壓縮在0和1之間。
$$\mathrm{p(x)=\frac{1}{1+e^-({\alpha_{0}+\alpha_{1}}x)}}$$
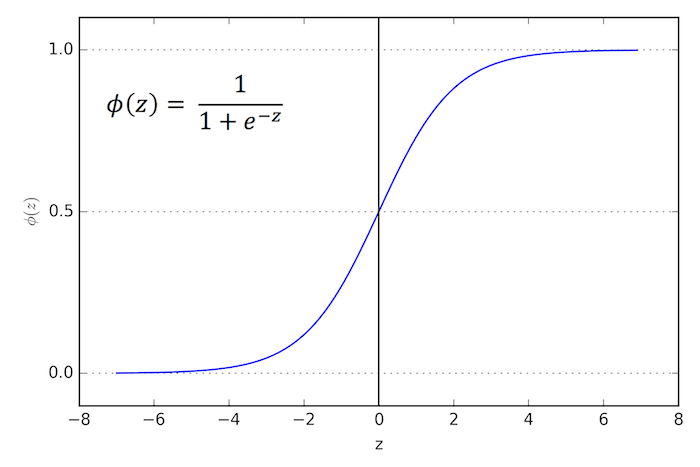
因此，我們可以使用邏輯迴歸對兩類進行建模。
邏輯函式或 sigmoid 函式是$\mathrm{\frac{1}{1+e^{−t}}}$。對數機率是邏輯函式的倒數。從線性迴歸方程中，我們看到它可以輸出從負無窮大到正無窮大的實數值，以及0,1邊界內的值。但是，在我們用 sigmoid 函式轉換線性迴歸方程後，轉換後的函式的機率值開始落在0和1之間。這證明了邏輯迴歸是一種分類演算法，不能用於迴歸。換句話說，邏輯迴歸根據邊界或類別對線性迴歸的值進行分類。
多類別分類邏輯迴歸
使用邏輯迴歸，我們可以實現多類別分類。對於二元和多類別分類，核心思想相同，但在多類別分類中，我們使用一對多分類的概念。根據以下等式，將有多個自變數：
$$\mathrm{\log\frac{p}{1−p}=\alpha_{0}+\alpha_{1}x_{1}+\alpha_{2}x_{2}+\alpha_{3}x_{3}+........+\alpha_{n}x_{n}}$$
在上式中，我們可以看到對數機率的值取決於n個自變數。
結論
邏輯迴歸是一種分類演算法，它輸出0和1之間的機率值，而不是連續值。這是由於對線性迴歸方程應用了 sigmoid 函式轉換。邏輯迴歸可用於二元和多類別分類。
147 次瀏覽
