機器學習中線性代數的應用

---

機器學習很大程度上依賴於線性代數，線性代數幫助建立了我們今天使用的基本模型和演算法。可以將其想象成機器用來解釋和理解複雜資料的語言。如果沒有線性代數，機器學習就像在沒有地圖或指南針的情況下試圖穿越一片茂密的森林。它為我們提供了有效表示和操作資料、提取有見地的結論以及改進模型的工具。透過線性代數，我們可以使用向量、矩陣以及矩陣乘法和分解等運算，從而釋放機器學習的真正潛力。因此，無論您是在探索迴歸、降維還是深度學習，理解線性代數都是成為熟練的機器學習從業人員的關鍵第一步。在本文中，我們將探討線性代數在機器學習中的應用。

理解線性代數

線性代數是支撐許多機器學習技術的數學基礎。線性代數處理向量、矩陣和相關運算，使我們能夠以結構化的方式管理和分析資料。

第一種量是向量，它們是既有大小又有方向的量。線上性代數的上下文中，向量可以表示各種物件，包括資料點、特徵或變數。可以使用運算（如加法、減法和標量乘法）對向量進行操作，以縮放或更改其值。

現在讓我們談談矩陣。它們只是按行和列排列的數字的矩形陣列。矩陣表示資料是一種強大的工具，尤其是在處理多個變數或特徵時。矩陣中的加法、減法和乘法運算使我們能夠以結構化的方式混合、變換和分析資料。

我們線上性代數中探索的另一個概念是向量空間。向量空間是一組滿足特定條件的向量。它為理解向量的屬性和關係提供了數學基礎。透過向量空間，我們可以定義線性代數中的基本運算，如向量加法和標量乘法。

線性變換的概念線上性代數中也很重要。這些函式在不同的向量空間之間轉換向量，同時考慮某些屬性。線性變換在機器學習中起著至關重要的作用，因為它們使我們能夠執行重塑或變換資料的操作，並以多種方式表示資料。

機器學習演算法中的線性代數

線性迴歸

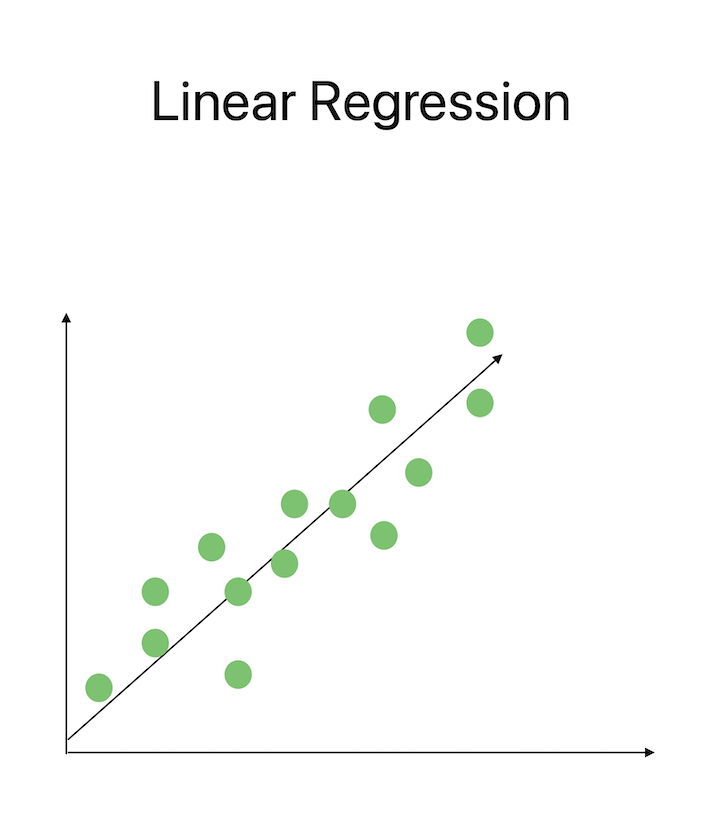
線性迴歸是一個重要的機器學習方法，它使用數學概念來表示輸入特徵和目標變數之間的關係。透過使用矩陣運算求解線性方程組，我們可以確定最佳係數，以最小化誤差併為資料提供最佳擬合。

主成分分析（PCA）

PCA是一種常見的機器學習降維方法。它使用線性代數，特別是特徵值和特徵向量，將高維資料轉換為低維空間，同時保留最重要的資訊。PCA透過分解協方差矩陣來識別資料中的潛在結構和趨勢。

支援向量機

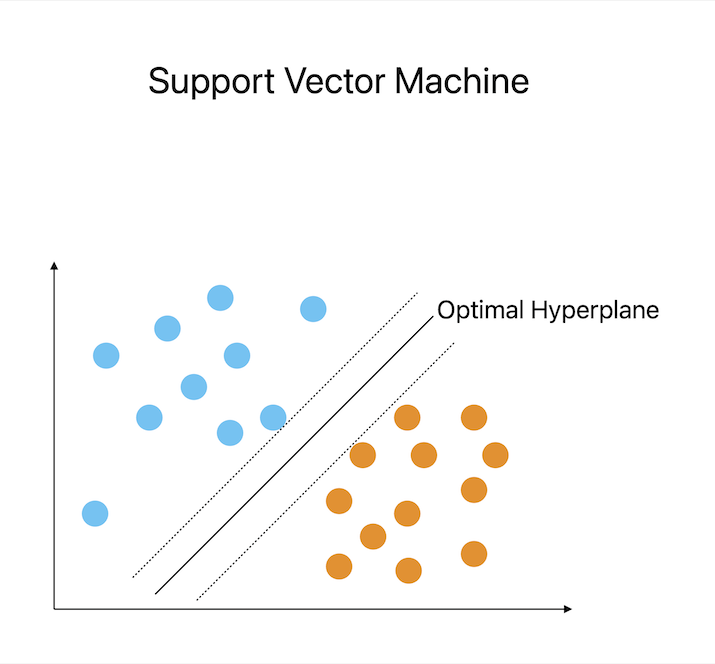
支援向量機利用線性代數來確定最佳超平面，將資料點分類到多個類別中。支援向量機將資料點表示為向量，並使用線性代數技術（如點積和矩陣運算），能夠有效地對新例項進行分類並處理複雜的決策邊界。

神經網路

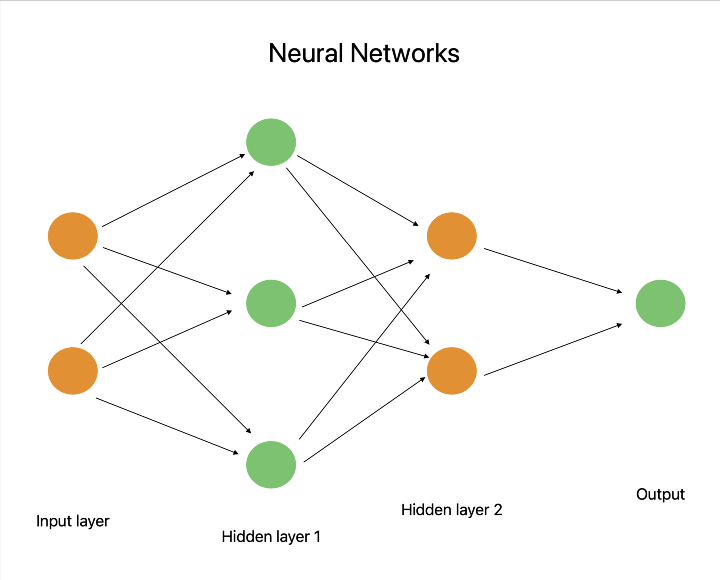
神經網路是深度學習的核心技術，它主要依賴於線性代數計算。在神經網路的前向和反向傳播過程中，使用矩陣乘法和啟用函式來表示作為矩陣的權重和偏差。這些線性代數過程使神經網路能夠學習複雜模式並做出準確預測。

線性代數的應用

影像識別和計算機視覺

線上性代數在影像識別問題中至關重要。卷積神經網路（CNN）等方法使用線性代數運算（如矩陣卷積和池化）從影像中提取特徵。這些演算法將影像表示為矩陣或張量，並在其上執行線性代數運算，能夠實現非常準確的物件識別、模式檢測和影像分類。

自然語言處理和文字分析

文字分析和自然語言處理（NLP）都嚴重依賴於線性代數。Word2Vec 和 GloVe 等詞嵌入將單詞表示為高維向量，捕獲單詞之間的語義關係。這些基於線性代數概念（如特徵分解和矩陣分解）的嵌入使 NLP 系統能夠理解和解釋文字輸入、執行情感分析，甚至生成語言。

推薦系統和協同過濾

推薦系統使用線性代數技術（如協同過濾）來生成個性化建議。這些系統透過將使用者-專案互動建模為矩陣並使用矩陣分解技術（如奇異值分解 (SVD)），可以識別相似的使用者和專案，並根據他們的偏好和行為提供準確的建議。

異常檢測和聚類演算法

異常檢測和聚類演算法利用線性代數的概念來查詢異常模式或對相關資料點進行分組。諸如 k 均值聚類和譜聚類等方法使用線性代數中的矩陣運算和特徵向量來將資料劃分為不同的組或識別異常值。

結論

總之，線性代數在機器學習中的價值不可估量。它是許多演算法和方法的基礎，使我們能夠有效地表示、操作和分析資料。線性代數可以求解複雜方程、降低維度並對變數之間的關係進行建模。它透過釋放矩陣運算、特徵向量和向量空間的強大功能，使我們能夠發現趨勢、做出準確預測並改進模型。