資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法學Python中的區域性加權線性迴歸
區域性加權線性迴歸是一種非引數方法/演算法。線上性迴歸中，資料應呈線性分佈，而區域性加權迴歸適用於非線性分佈的資料。通常，在區域性加權迴歸中，距離查詢點較近的點比距離較遠的點權重更大。
引數模型和非引數模型
引數模型
引數模型是將函式簡化為已知形式的模型。它具有一組引數，透過這些引數來總結資料。
這些引數的數量是固定的，這意味著模型已經知道這些引數，並且它們不依賴於資料。它們在訓練樣本方面也是獨立的。
例如，讓我們假設一個如下所述的對映函式。
b0+b1x1+b2x2=0
從等式中，b0、b1和b2是控制截距和斜率的直線係數。輸入變數由x1和x2表示。
非引數模型
非引數演算法不對對映函式的型別做出特別的假設。這些演算法不接受輸入和輸出資料之間特定形式的對映函式為真。
它們可以自由地從訓練資料中選擇任何函式形式。因此，與引數模型相比，引數模型需要更多的資料來估計對映函式。
代價函式和權重的推導
線性迴歸的代價函式是
$$\mathrm{\displaystyle\sum\limits_{i=1}^m (y^{{(i)}} \:-\:\Theta^Tx)^2}$$
在區域性加權線性迴歸中，代價函式被修改為
$$\mathrm{\displaystyle\sum\limits_{i=1}^m w^i(y^{{(i)}} \:-\:\Theta^Tx)^2}$$
其中𝑤(𝑖)表示第i個訓練樣本的權重。
權重函式可以定義為
$$\mathrm{w(i)\:=\:exp\:(-\frac{(x^i-x)^2}{2\tau^2})}$$
x是我們想要進行預測的點。x(i)是第i個訓練樣本
τ可以稱為權重函式的高斯鐘形曲線的頻寬。
τ的值可以調整以根據與查詢點的距離改變w的值。
τ 的小值意味著資料點到查詢點的距離較小，w 的值變大（權重更大），反之亦然。
w 的值通常在 0 到 1 之間。
區域性加權迴歸演算法沒有訓練階段。所有權重θ都在預測階段確定。
示例
讓我們考慮一個包含以下點的dataset
2,5,10,17,26,37,50,65,82
將查詢點設為 x = 7，並從資料集中取三個點 5, 10, 26
因此 x(1) = 5, x(2) = 10, x(3) = 26。設 τ = 0.5
因此，
$$\mathrm{w(1) = exp( - ( 5 – 7 )^2 / (2 x 0.5^2)) = 0.00061}$$
$$\mathrm{w(2) = exp( - (10 – 7 )^2 / (2 x 0.5^2)) = 5.92196849e-8}$$
$$\mathrm{w(3) = exp( - (26 – 7 )^2 / (2 x 0.5^2)) = 1.24619e-290}$$
$$\mathrm{J(\Theta) = 0.00061 * (\Theta^ T x(1) – y(1) ) + 5.92196849e-8 * (\Theta^ T x(2) – y(2) ) + 1.24619e-290 *( \Theta^ T x(3) – y(3) )}$$
從上面的例子可以看出，查詢點 (x) 與特定資料點/樣本x(1), x(2), x(3)等的距離越近，w 的值越大。對於遠離查詢點的數 據點，權重呈指數下降。
隨著 x(i) 和 x 之間距離的增加，權重減小。這減少了誤差項對代價函式的貢獻，反之亦然。
Python 實現
下面的程式碼片段演示了局部加權線性迴歸演算法。
tips 資料集可以從 這裡 下載
示例
import pandas as pd import numpy as np import matplotlib.pyplot as plt %matplotlib inline df = pd.read_csv('/content/tips.csv') features = np.array(df.total_bill) labels = np.array(df.tip) def kernel(data, point, xmat, k): m,n = np.shape(xmat) ws = np.mat(np.eye((m))) for j in range(m): diff = point - data[j] ws[j,j] = np.exp(diff*diff.T/(-2.0*k**2)) return ws def local_weight(data, point, xmat, ymat, k): wei = kernel(data, point, xmat, k) return (data.T*(wei*data)).I*(data.T*(wei*ymat.T)) def local_weight_regression(xmat, ymat, k): m,n = np.shape(xmat) ypred = np.zeros(m) for i in range(m): ypred[i] = xmat[i]*local_weight(xmat, xmat[i],xmat,ymat,k) return ypred m = features.shape[0] mtip = np.mat(labels) data = np.hstack((np.ones((m, 1)), np.mat(features).T)) ypred = local_weight_regression(data, mtip, 0.5) indices = data[:,1].argsort(0) xsort = data[indices][:,0] fig = plt.figure() ax = fig.add_subplot(1,1,1) ax.scatter(features, labels, color='blue') ax.plot(xsort[:,1],ypred[indices], color = 'red', linewidth=3) plt.xlabel('Total bill') plt.ylabel('Tip') plt.show()
輸出
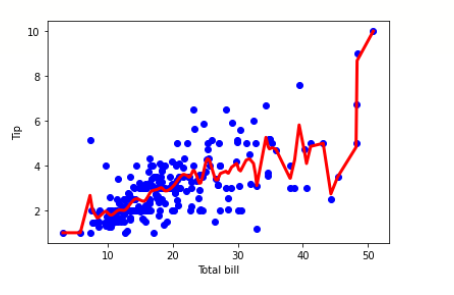
什麼時候可以使用區域性加權線性迴歸？
當特徵數量較少時。
當不需要特徵選擇時。
區域性加權線性迴歸的優點。
在區域性加權線性迴歸中，區域性權重是相對於每個資料點計算的，因此出現較大誤差的可能性較小。
我們擬合一條曲線，因此誤差最小化。
在這個演算法中，有很多小的區域性函式，而不是一個要最小化的全域性函式。區域性函式在調整變化和誤差方面更有效。
區域性加權線性迴歸的缺點。
這個過程非常耗時，可能會消耗大量的資源。
對於線性相關的簡單問題，我們可以簡單地避免使用區域性加權演算法。
無法容納大量的特徵。
結論
因此，簡而言之，區域性加權線性迴歸更適合於資料呈非線性分佈，並且我們仍然希望使用迴歸模型擬合數據而不會影響預測質量的情況。
瀏覽量：5000+
