線性迴歸假設 - 同方差性

---

簡介

線性迴歸是機器學習中最常用和最簡單的演算法之一，它可以幫助預測幾乎所有型別問題陳述中的線性資料。雖然線性迴歸是一種引數化機器學習演算法，但該演算法假設資料滿足某些假設，以便更快更容易地進行預測。同方差性也是線性迴歸的核心假設之一，在對相應資料集應用線性迴歸時，假定該假設得到滿足。在本文中，我們將討論線性迴歸的同方差性假設、其核心思想、其重要性和一些其他相關的重要內容。

在本文中，我們將討論線性迴歸的行為模式，為什麼它是一種引數化演算法，什麼是同方差性，以及它為什麼很重要。本文將幫助讀者瞭解線性迴歸的引數化行為，並能夠理解線性迴歸的同方差性假設。

假設的必要性

在開始討論線性迴歸所假設的假設之前，有必要了解為什麼我們要假設這些東西；這樣做的必要性是什麼？

要更好地理解這個概念，有必要首先了解引數化模型。引數化模型是機器學習中的一種演算法型別，其工作原理是使用用於訓練它們的函式，並且它們根據該函式得出輸出結果。由於該函式用於訓練和預測演算法，因此並非每個資料點或資料集都可以直接應用，因此為了使過程更易於訪問和更高效，我們假設某些事情，然後構建相應的函式。

例如，線性迴歸是一種引數化演算法，它假設資料是線性和同方差的。

什麼是同方差性？

同方差性是線性迴歸的假設之一，其中殘差的方差假定為常數。簡單來說，在誤差與預測變數的圖形或誤差中，誤差項應具有恆定的方差，並且誤差項的值不應隨著預測變數值的改變而改變。

同方差性的反面是異方差性，其中誤差項或殘差根據預測變數並非恆定，並且誤差項隨著預測變數值的改變而迅速變化。

眾所周知，線上性迴歸中，使用線性方程來解決資料模式問題，即 Y = mX + c，其中 m 和 c 為常數，X 為自變數，y 為因變數。

現在，這裡我們將有一些被認為是真實值的因變數 Y 值，並且我們還將使用自變數 X 預測 Y 的值，這將被稱為變數 Y 的預測值。

這裡的誤差項僅僅是變數 Y 的真實值與變數 Y 的預測值之間的差值。其中同方差性表示誤差項與預測變數 Y 之間的恆定方差。

同方差性示例

讓我們嘗試透過舉例來理解同方差性的概念，以闡明其背後的所有核心直覺。

假設您想根據特定學生學習該科目所花費的小時數來預測該學生的成績。因此，在這種情況下，學生的成績將成為我們的因變數，它將取決於小時數變數，而自變數或變數將是特定學生學習該科目所花費的小時數。

現在，讓我們假設我們擁有的是線性資料，並且我們將使用線性迴歸來解決該問題。在這裡，在這種情況下，將生成一條最佳擬合線，這將是迴歸線，它也可以為未知資料提供學生成績的線索。

但是，由於您已經建立了一個預測學生成績的模型，因此您將檢查模型的準確性以驗證演算法並在需要時進行更改。現在，為了驗證模型，您將透過計算學生成績的實際值和學生成績的預測值之間的差值來計算模型產生的誤差。

現在，如果您想檢查模型是否遵循同方差性，則可以在誤差項（殘差）與預測變數 Y（學生的預測成績）之間繪製圖形（散點圖）。

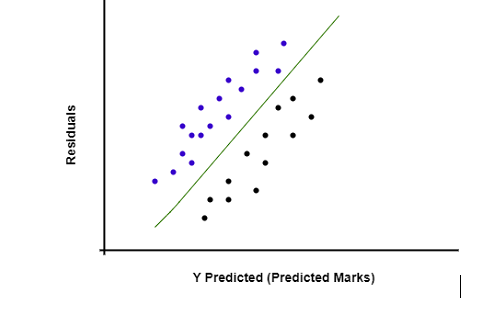
正如我們在上圖中看到的，繪製了預測成績或因變數與殘差之間的散點圖，其中散佈或方差是恆定的，這意味著該模型遵循同方差性並且令人滿意。

同方差性的重要性

同方差性是線性迴歸的假設之一。我們知道線性迴歸是一種引數化模型，它需要滿足其假設，因此如果我們正在應用線性迴歸。如果該假設不滿足，則構建的模型將非常糟糕且準確性較低。

此外，同方差性使我們能夠了解誤差項相對於預測變數的散佈或方差；透過分析同方差性圖，我們可以輕鬆識別模型產生較大誤差和錯誤的位置，這會影響模型的整體效能。

關鍵要點

• 線性迴歸是一種引數化模型，它假設資料和模型滿足某些假設。

• 同方差性是定義誤差項與預測變數之間的圖形上具有相等方差的術語。

• 異方差模型在誤差與預測變數的圖形上沒有相等的方差。

• 同方差性圖使我們能夠了解模型產生較大誤差的位置，並且可以對其進行修復。

• 遵循同方差性的模型對於線性迴歸演算法來說是令人滿意的。

結論

在本文中。我們透過討論其他重要術語（如引數化模型、為什麼需要假設以及相應的示例）來討論線性迴歸演算法的同方差性假設。本文將幫助讀者更好地理解同方差性的概念，並能夠非常有效地回答與之相關的面試問題，這些問題通常會被問到。