資料結構
網路
RDBMS
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律學萊布尼茨調和三角形
萊布尼茨調和三角形，也稱為萊布尼茨級數或萊布尼茨公式，是由德國數學家和哲學家戈特弗裡德·威廉·萊布尼茨在17世紀後期發現的一種三角形排列的數字。
萊布尼茨調和三角形是由分陣列成的三角形排列。我們從頂部開始，數字為1，最外層的項是表示該特定行號的自然數的倒數。一般來說，萊布尼茨調和三角形中的一個項可以透過以下等式確定，其中r是行號，c是列號，條件是c <= r
L(r,c)=L(r-1,c-1) - L(r,c-1)，其中L(r,1)=1/r
下圖描繪了萊布尼茨調和三角形的前3行。
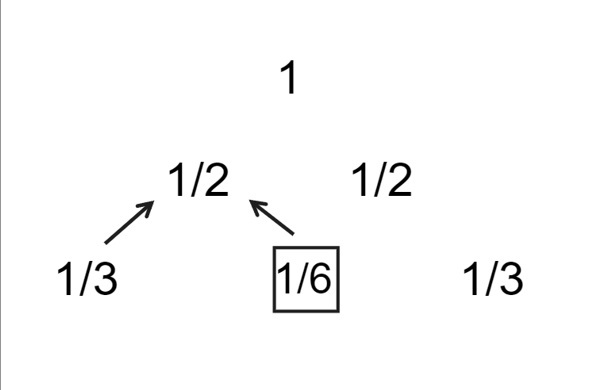
問題陳述
給定一個數字n，生成n行的萊布尼茨調和三角形。
示例
輸入
n = 3
輸出
1/1 1/2 1/2 1/3 1/6 1/3
解釋
對於n = 3，萊布尼茨調和三角形有三行。每行的最外層項 = 1/(行號)。
為了生成這個三角形，我們從第一行開始，它為1/1。然後，對於第二行，我們將每個單元格的值計算為左上方對角線上的單元格減去左邊的單元格
L(2, 1) = 1/2
L(2, 2) = 1/2
所以第二行是1/2 1/2。
最後，對於第三行，我們再次將每個單元格的值計算為左上方對角線上的單元格減去左邊的單元格
L(3,1) = L(3,3) = 1/3
L(3,2) = L(2,1) - L(3,1) = 1/6
輸入
n = 4
輸出
1/1 1/2 1/2 1/3 1/6 1/3 1/4 1/12 1/12 1/4
解釋
直到n = 3，方法與上述示例相同。
對於第四行
L(4,1) = L(4,4) = 1/4
L(4,2) = L(3,1) - L(4,1) = 1/3 - 1/4 = 1/12
L(4,3) = L(3,2) - L(4,2) = 1/6 - 1/12 = 1/12
解決方案方法
虛擬碼
開始
將n的值初始化為4。
宣告一個二維向量L，具有n+1行和n+1列，並將所有元素初始化為0。
呼叫函式LHT，引數為n和L。
在函式LHT中，迭代從i=0到i<=n。
在上述迴圈中，迭代從j=0到j<=min(i,n)。
在上述迴圈中，如果j==0或j==i，則將L[i][j]的值設定為1。
否則，將L[i][j]的值設定為L[i-1][j-1]+L[i-1][j]。
呼叫函式printLHT，引數為n和L。
在函式printLHT中，迭代從i=1到i<=n。
在上述迴圈中，迭代從j=1到j<=i。
在上述迴圈中，列印“1/”，後跟i*L[i-1][j-1]。
在每個內部迴圈完成後列印一個新行。
結束。
演算法
function LHT()
for i = 0 to n do
for j = 0 to min(i, n) do
if j == 0 or j == i then
L[i][j] = 1
else
L[i][j] = L[i-1][j-1] + L[i-1][j]
end if
end for
end for
printLHT(n, L)
end function
function printLHT()
for i = 1 to n do
for j = 1 to i do
print "1/" + i*L[i-1][j-1] + " "
end for
print new line
end for
end function
function main
Initialize n = 4
L = 2D vector of size n + 1 x n + 1, with all elements initialized to 0
LHT(n, L)
return 0
示例：C++程式
以下C++程式使用函式LHT()和printLHT()生成並列印給定行數的萊布尼茨調和三角形。main()函式初始化行數並建立一個大小為n + 1 * n + 1的二維向量‘L’來儲存項。
// CPP Program to print Leibniz Harmonic Triangle
#include <bits/stdc++.h>
using namespace std;
// Function to print Leibniz Harmonic Triangle
void printLHT(int n, vector<vector<int>> L){
for (int i = 1; i <= n; i++){
for (int j = 1; j <= i; j++)
cout << "1/" << i * L[i - 1][j - 1] << " ";
cout << endl;
}
}
// Function to generate Leibniz Harmonic Triangle
void LHT(int n, vector<vector<int>> &L){
for (int i = 0; i <= n; i++){
for (int j = 0; j <= min(i, n); j++){
if (j == 0 || j == i)
L[i][j] = 1;
// Generate the value using previously stored values
else
L[i][j] = L[i - 1][j - 1] + L[i - 1][j];
}
}
// print Leibniz Harmonic Triangle
printLHT(n,L);
}
// Main function
int main(){
int n = 5;
// 2D vector to store the Leibniz Harmonic Triangle
vector<vector<int>> L(n + 1, vector<int>(n + 1, 0));
LHT(n, L);
return 0;
}
輸出
1/1 1/2 1/2 1/3 1/6 1/3 1/4 1/12 1/12 1/4 1/5 1/20 1/30 1/20 1/5
時間和空間複雜度分析
時間複雜度：O(n2)
此程式的時間複雜度為O(n2)，其中n是萊布尼茨調和三角形中的行數。這是因為該程式透過計算每個條目作為兩個先前條目的和來生成三角形，並且三角形中有n2個條目。
空間複雜度：O(n2)
此程式的空間複雜度也為O(n2)，因為它將整個三角形儲存在一個大小為(n + 1) * (n + 1)的二維向量中。
結論
在本文中，我們討論了一種生成直到給定行數的萊布尼茨調和三角形的方法。萊布尼茨調和三角形是一個有趣的數學概念，類似於帕斯卡三角形。討論了概念、實現、解決方案方法以及虛擬碼、使用的演算法和C++程式。我們還分析了我們解決方案的時間和空間複雜度。
149 次檢視
