資料結構
網路
關係資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
服裝設計
法律研究如果點\( A(1,-2), B(2,3) C(a, 2) \)和\( D(-4,-3) \)構成一個平行四邊形。求\( a \)的值以及以AB為底的平行四邊形的高。
已知
點 $A (1, -2), B (2, 3), C (a, 2)$ 和 $D (-4, -3)$ 構成一個平行四邊形。
要求
我們必須找到 $a$ 的值以及以 $AB$ 為底的平行四邊形的高。
解
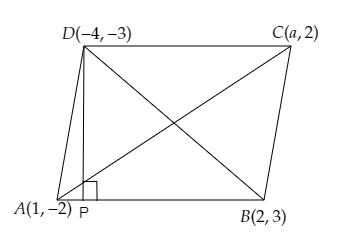
從\( \mathrm{D} \)向\( \mathrm{AB} \)作垂線，垂足為\( \mathrm{P} \)。
\( \mathrm{DP} \)是平行四邊形的高。
我們知道，
平行四邊形的對角線互相平分。
這意味著，
$AC$ 的中點 = $BD$ 的中點
連線點\( \left(x_{1}, y_{1}\right) \)和\( \left(x_{2}, y_{2}\right) \)的線段的中點是\( (\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}) \)
\( (\frac{1+a}{2}, \frac{-2+2}{2})=(\frac{2-4}{2}, \frac{3-3}{2}) \)
比較後，我們得到：
\( \Rightarrow \frac{1+a}{2}=\frac{-2}{2}=-1 \)
\( \Rightarrow 1+a=-2 \)
\( \Rightarrow a=-3 \)
所需的\( a \)值為\( -3 \)。
我們知道，
對角線將三角形分成兩個面積相等的三角形。
這意味著，
平行四邊形 $ABCD$ 的面積 = 三角形 $ABC$ 的面積 + 三角形 $ADC$ 的面積。
$=2\times$ 三角形 $ABC$ 的面積
我們知道，
頂點為 $(x_1,y_1), (x_2,y_2), (x_3,y_3)$ 的三角形的面積由以下公式給出：
三角形面積 $\Delta=\frac{1}{2}[x_{1}(y_{2}-y_{3})+x_{2}(y_{3}-y_{1})+x_{3}(y_{1}-y_{2})]$
因此，
三角形\( ABC \)的面積=\(\frac{1}{2}[1(3-2)+2(2+2)+(-3)(-2-3)] \)
\( =\frac{1}{2}[1(1)+(2)(4)+(-3)(-5)] \)
\( =\frac{1}{2}[1+8+15] \)
\( =\frac{1}{2} \times (24) \)
\( =12 \) 平方單位。
因此，
平行四邊形 $ABCD$ 的面積 $=2\times 12=24$ 平方單位。
平行四邊形的面積 = 底 $\times$ 高
高 = 面積 $\div$ 底
$DP=\frac{24}{AB}$
根據距離公式，我們得到：
$AB=\sqrt{(2-1)^2+(3+2)^2}$
$=\sqrt{1^2+5^2}$
$=\sqrt{1+25}$
$=\sqrt{26}$
因此，
$DP=\frac{24}{\sqrt{26}}$
$=\frac{24\times\sqrt{26}}{\sqrt{26}\times\sqrt{26}}$
$=\frac{24\sqrt{26}}{26}$
$=\frac{12\sqrt{26}}{13}$
以 $AB$ 為底的平行四邊形的高是 $\frac{12\sqrt{26}}{13}$。
53 次瀏覽
