資料結構
網路
關係資料庫管理系統 (RDBMS)
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C語言程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化學
生物
數學
英語
經濟學
心理學
社會研究
時尚研究
法律研究如果\( \sin \mathrm{A}=\frac{1}{2} \)，則\( \cot \mathrm{A} \)的值為
(A) \( \sqrt{3} \)
(B) \( \frac{1}{\sqrt{3}} \)
(C) \( \frac{\sqrt{3}}{2} \)
(D) 1
已知
$\sin\ A = \frac{1}{2}$
求解
我們需要求\( \cot\ A \)的值。
解：
設在直角三角形\(ABC\)中，\( \angle B = 90^\circ \)，\( \sin\ A=\frac{1}{2}\)。
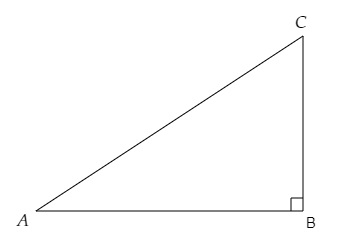
我們知道：
在以B為直角的直角三角形ABC中，
根據勾股定理，
\(AC^2=AB^2+BC^2\)
根據三角函式定義，
\( \sin\ \theta=\frac{對邊}{斜邊}=\frac{BC}{AC} \)
\( \cos\ \theta=\frac{鄰邊}{斜邊}=\frac{AB}{AC} \)
\( \sec\ \theta=\frac{斜邊}{鄰邊}=\frac{AC}{AB} \)
\( \tan\ \theta=\frac{對邊}{鄰邊}=\frac{BC}{AB} \)
\( \cot\ \theta=\frac{鄰邊}{對邊}=\frac{AB}{BC} \)
這裡，
\(AC^2=AB^2+BC^2\)
\( \Rightarrow AC = 2, BC = 1 \)
\( \Rightarrow (2)^2=(AB)^2+1^2 \)
\( \Rightarrow AB^2=4-1 \)
\( \Rightarrow AB=\sqrt{3} \)
因此，
\( \cot\ A=\frac{AB}{BC}=\frac{\sqrt{3}}{1} \)
更新於：2022年10月10日
56 次瀏覽
廣告