如果 $cos\ A = \frac{4}{5}$，那麼 $tan\ A$ 的值是
(A) $\frac{3}{5}$
(B) $\frac{3}{4}$
(C) $\frac{4}{3}$
(D) $\frac{5}{3}$

已知

$cos\ A = \frac{4}{5}$

求解

我們需要求 $tan\ A$ 的值。

解：  

設在直角三角形 $ABC$ 中，$\angle B = 90°$，$cos\ A=\frac{4}{5}$。

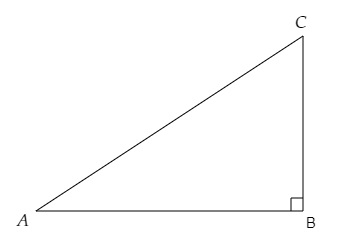
我們知道：

在以 $B$ 為直角的直角三角形 $ABC$ 中，

根據勾股定理，

$AC^2=AB^2+BC^2$

根據三角函式定義，

$sin\ \theta=\frac{對邊}{斜邊}=\frac{BC}{AC}$

$cos\ \theta=\frac{鄰邊}{斜邊}=\frac{AB}{AC}$

$sec\ \theta=\frac{斜邊}{鄰邊}=\frac{AC}{AB}$

$tan\ \theta=\frac{對邊}{鄰邊}=\frac{BC}{AB}$

這裡，

$AC^2=AB^2+BC^2$

$\Rightarrow (5)^2=(4)^2+BC^2$

$\Rightarrow BC^2=25-16$

$\Rightarrow BC=\sqrt{9}=3$

因此，

$tan\ A=\frac{BC}{AB}=\frac{3}{4}$。

教程點

更新於：2022年10月10日

64 次瀏覽

開啟你的職業生涯

完成課程獲得認證

開始學習