
- C語言資料結構與演算法教程
- C語言資料結構與演算法 - 首頁
- C語言資料結構與演算法 - 概述
- C語言資料結構與演算法 - 環境配置
- C語言資料結構與演算法 - 演算法
- C語言資料結構與演算法 - 概念
- C語言資料結構與演算法 - 陣列
- C語言資料結構與演算法 - 連結串列
- C語言資料結構與演算法 - 雙向連結串列
- C語言資料結構與演算法 - 迴圈連結串列
- C語言資料結構與演算法 - 棧
- C語言資料結構與演算法 - 表示式解析
- C語言資料結構與演算法 - 佇列
- C語言資料結構與演算法 - 優先佇列
- C語言資料結構與演算法 - 樹
- C語言資料結構與演算法 - 雜湊表
- C語言資料結構與演算法 - 堆
- C語言資料結構與演算法 - 圖
- C語言資料結構與演算法 - 搜尋技術
- C語言資料結構與演算法 - 排序技術
- C語言資料結構與演算法 - 遞迴
- C語言資料結構與演算法 - 有用資源
- C語言資料結構與演算法 - 快速指南
- C語言資料結構與演算法 - 有用資源
- C語言資料結構與演算法 - 討論
C語言資料結構與演算法 - 快速指南
C語言資料結構與演算法 - 概述
什麼是資料結構?
資料結構是以一種可以有效使用的方式組織資料的方法。以下術語是資料結構的基礎術語。
介面 - 每個資料結構都有一個介面。介面表示資料結構支援的一組操作。介面僅提供支援的操作列表、它們可以接受的引數型別以及這些操作的返回型別。
實現 - 實現提供了資料結構的內部表示。實現還提供了資料結構操作中使用的演算法的定義。
資料結構的特性
正確性 - 資料結構實現應正確實現其介面。
時間複雜度 - 資料結構操作的執行時間或執行時間應儘可能短。
空間複雜度 - 資料結構操作的記憶體使用量應儘可能少。
資料結構的必要性
隨著應用程式越來越複雜和資料豐富,如今應用程式面臨三個常見問題。
資料搜尋 - 考慮一個商店擁有100萬(106)件商品的庫存。如果應用程式要搜尋一件商品,它每次都必須在100萬(106)件商品中搜索商品,從而減慢搜尋速度。隨著資料量的增長,搜尋會變得越來越慢。
處理器速度 - 儘管處理器速度非常高,但如果資料增長到數十億條記錄,處理器速度仍然有限。
多個請求 - 由於數千個使用者可以同時在一個 Web 伺服器上搜索資料,即使是速度非常快的伺服器在搜尋資料時也會失敗。
為了解決上述問題,資料結構可以提供幫助。資料可以以這樣一種方式組織在資料結構中,使得可能不需要搜尋所有專案,並且可以幾乎立即搜尋所需的資料。
執行時間情況
通常使用三種情況來相對比較各種資料結構的執行時間。
最壞情況 - 這是一種場景,其中特定資料結構操作花費可能花費的最長時間。如果操作的最壞情況時間為 ƒ(n),則此操作不會花費超過 ƒ(n) 時間,其中 ƒ(n) 表示 n 的函式。
平均情況 - 這是一種場景,描述了資料結構操作的平均執行時間。如果一個操作需要 ƒ(n) 時間執行,則 m 個操作將需要 mƒ(n) 時間。
最佳情況 - 這是一種場景,描述了資料結構操作的最小可能執行時間。如果一個操作需要 ƒ(n) 時間執行,則實際操作可能花費的時間是一個隨機數,其最大值為 ƒ(n)。
C語言資料結構與演算法 - 環境搭建
本地環境搭建
如果您仍然希望為 C 程式語言設定環境,則需要在您的計算機上安裝以下兩種軟體:(a) 文字編輯器和 (b) C 編譯器。
文字編輯器
這將用於鍵入您的程式。一些編輯器的示例包括 Windows 記事本、OS Edit 命令、Brief、Epsilon、EMACS 和 vim 或 vi。
文字編輯器的名稱和版本在不同的作業系統上可能有所不同。例如,Notepad 將在 Windows 上使用,而 vim 或 vi 也可以在 Windows 以及 Linux 或 UNIX 上使用。
您使用編輯器建立的檔案稱為原始檔,其中包含程式原始碼。C 程式的原始檔通常以副檔名“.c”命名。
在開始程式設計之前,請確保您已準備好一個文字編輯器,並且您有足夠的經驗來編寫計算機程式,將其儲存在檔案中,編譯它並最終執行它。
C 編譯器
原始檔中編寫的原始碼是程式的人類可讀原始碼。它需要“編譯”才能轉換為機器語言,以便您的 CPU 能夠根據給定的指令實際執行程式。
此 C 程式語言編譯器將用於將您的原始碼編譯成最終的可執行程式。我假設您瞭解程式語言編譯器的基本知識。
最常用的免費編譯器是 GNU C/C++ 編譯器,如果您有相應的作業系統,也可以使用 HP 或 Solaris 的編譯器。
以下部分指導您如何在各種作業系統上安裝 GNU C/C++ 編譯器。我同時提及 C/C++,因為 GNU gcc 編譯器適用於 C 和 C++ 程式語言。
在 UNIX/Linux 上安裝
如果您使用的是Linux 或 UNIX,請透過從命令列輸入以下命令來檢查您的系統上是否安裝了 GCC:
$ gcc -v
如果您的計算機上安裝了 GNU 編譯器,則它應該列印如下訊息:
Using built-in specs. Target: i386-redhat-linux Configured with: ../configure --prefix=/usr ....... Thread model: posix gcc version 4.1.2 20080704 (Red Hat 4.1.2-46)
如果未安裝 GCC,則您必須使用https://gcc.gnu.org/install/上提供的詳細說明自行安裝。
本教程是基於 Linux 編寫的,所有給出的示例都在 Cent OS 版本的 Linux 系統上編譯。
在 Mac OS 上安裝
如果您使用的是 Mac OS X,獲取 GCC 的最簡單方法是從 Apple 的網站下載 Xcode 開發環境,然後按照簡單的安裝說明進行操作。設定 Xcode 後,您將能夠使用 GNU C/C++ 編譯器。
Xcode 目前可在developer.apple.com/technologies/tools/獲取。
在 Windows 上安裝
要在 Windows 上安裝 GCC,您需要安裝 MinGW。要安裝 MinGW,請訪問 MinGW 主頁 www.mingw.org,然後點選連結進入 MinGW 下載頁面。下載最新版本的 MinGW 安裝程式,其名稱應為 MinGW-<version>.exe。
安裝 MinWG 時,至少必須安裝 gcc-core、gcc-g++、binutils 和 MinGW 執行時,但您可能希望安裝更多內容。
將 MinGW 安裝的 bin 子目錄新增到您的PATH環境變數中,以便您可以透過簡單的名稱在命令列中指定這些工具。
安裝完成後,您將能夠從 Windows 命令列執行 gcc、g++、ar、ranlib、dlltool 和其他幾個 GNU 工具。
C語言資料結構與演算法 - 演算法
演算法
演算法是一個逐步的過程,它定義了一組指令,這些指令以一定的順序執行以獲得預期的輸出。就資料結構而言,演算法分為以下幾類。
搜尋 - 在資料結構中搜索專案的演算法。
排序 - 按特定順序對專案進行排序的演算法
插入 - 將專案插入資料結構的演算法
更新 - 更新資料結構中現有專案的演算法
刪除 - 從資料結構中刪除現有專案的演算法
演算法分析
演算法分析處理的是資料結構各種操作的執行時間或執行時間。操作的執行時間可以定義為每個操作執行的計算機指令數。由於任何操作的確切執行時間因計算機而異,我們通常將任何操作的執行時間分析為 n 的某個函式,其中 n 是資料結構中該操作處理的專案數。
漸近分析
漸近分析是指使用數學計算單元來計算任何操作的執行時間。例如,一個操作的執行時間計算為 *f*(n),另一個操作的執行時間計算為 *g*(n2)。這意味著第一個操作的執行時間將隨著 n 的增加而線性增加,而第二個操作的執行時間將隨著 n 的增加而呈指數增長。同樣,如果 n 非常小,則這兩個操作的執行時間幾乎相同。
漸近符號
以下是計算演算法執行時間複雜度時常用的漸近符號。
Ο 符號
Ω 符號
θ 符號
大O符號,Ο
Ο(n) 是表達演算法執行時間上限的正式方法。它衡量的是最壞情況下的時間複雜度,或者演算法可能完成所需的最長時間。
例如,對於函式 *f*(n)
大O符號用於簡化函式。例如,我們可以用 Ο(*f*(nlogn)) 來代替特定的函式方程 7nlogn + n - 1。考慮如下場景:
這表明 *f*(n) = 7nlogn +n - 1 在使用常數 c = 8 和 n0 = 2 的 *O*(nlogn) 輸出範圍內。
歐米茄符號,Ω
Ω(n) 是表達演算法執行時間下界的正式方法。它衡量的是最佳情況下的時間複雜度,或者演算法可能完成所需的最短時間。
例如,對於函式 *f*(n)
西塔符號,θ
θ(n) 是表達演算法執行時間下界和上界的正式方法。它表示如下。
C語言資料結構與演算法 - 概念
資料結構是以一種可以有效使用的方式組織資料的方法。以下術語是資料結構的基本術語。
資料定義
資料定義使用以下特性定義特定資料。
原子性 - 定義應定義單個概念
可追溯性 - 定義應該能夠對映到某些資料元素。
準確性 - 定義應該明確。
清晰簡潔 - 定義應該易於理解。
資料物件
資料物件表示具有資料的物件。
資料型別
資料型別是對各種型別的資料(例如整數、字串等)進行分類的方式,它決定了可以與相應型別的資料一起使用的值,以及可以對相應型別的資料執行的操作。資料型別分為兩種:
內建資料型別
派生資料型別
內建資料型別
語言內建支援的那些資料型別稱為內建資料型別。例如,大多數語言提供以下內建資料型別。
整數
布林值(true,false)
浮點數(小數)
字元和字串
派生資料型別
那些實現獨立的資料型別,因為它們可以以一種或另一種方式實現,被稱為派生資料型別。這些資料型別通常由主資料型別或內建資料型別及其相關操作組合構建而成。例如:
列表
陣列
棧
佇列
使用 C 語言的 DSA - 陣列
概述
陣列是一個容器,它可以容納固定數量的項,並且這些項應該屬於同一型別。大多數資料結構都利用陣列來實現其演算法。以下是理解陣列概念的重要術語。
元素 - 儲存在陣列中的每個專案都稱為元素。
索引 - 陣列中每個元素的位置都有一個數值索引,用於標識該元素。
陣列表示
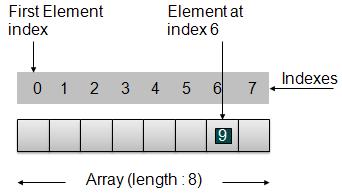
根據上圖所示,以下是需要考慮的重要幾點。
索引從 0 開始。
陣列長度為 8,這意味著它可以儲存 8 個元素。
每個元素都可以透過其索引訪問。例如,我們可以獲取索引為 6 的元素 9。
基本操作
以下是陣列支援的基本操作。
插入 - 在給定索引處新增元素。
刪除 - 刪除給定索引處的元素。
搜尋 - 使用給定索引或值搜尋元素。
更新 - 更新給定索引處的元素。
在 C 語言中,當陣列初始化大小後,它會按照以下順序為其元素分配預設值。
| 序號 | 資料型別 | 預設值 |
|---|---|---|
| 1 | bool | false |
| 2 | char | 0 |
| 3 | int | 0 |
| 4 | float | 0.0 |
| 5 | double | 0.0f |
| 6 | void | |
| 7 | wchar_t | 0 |
示例
#include <stdio.h>
#include <string.h>
static void display(int intArray[], int length){
int i=0;
printf("Array : [");
for(i = 0; i < length; i++) {
/* display value of element at index i. */
printf(" %d ", intArray[i]);
}
printf(" ]\n ");
}
int main() {
int i = 0;
/* Declare an array */
int intArray[8];
// initialize elements of array n to 0
for ( i = 0; i < 8; i++ ) {
intArray[ i ] = 0; // set elements to default value of 0;
}
printf("Array with default data.");
/* Display elements of an array.*/
display(intArray,8);
/* Operation : Insertion
Add elements in the array */
for(i = 0; i < 8; i++) {
/* place value of i at index i. */
printf("Adding %d at index %d\n",i,i);
intArray[i] = i;
}
printf("\n");
printf("Array after adding data. ");
display(intArray,8);
/* Operation : Insertion
Element at any location can be updated directly */
int index = 5;
intArray[index] = 10;
printf("Array after updating element at index %d.\n",index);
display(intArray,8);
/* Operation : Search using index
Search an element using index.*/
printf("Data at index %d:%d\n" ,index,intArray[index]);
/* Operation : Search using value
Search an element using value.*/
int value = 4;
for(i = 0; i < 8; i++) {
if(intArray[i] == value ){
printf("value %d Found at index %d \n", intArray[i],i);
break;
}
}
return 0;
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Array with default data.Array : [ 0 0 0 0 0 0 0 0 ] Adding 0 at index 0 Adding 1 at index 1 Adding 2 at index 2 Adding 3 at index 3 Adding 4 at index 4 Adding 5 at index 5 Adding 6 at index 6 Adding 7 at index 7 Array after adding data. Array : [ 0 1 2 3 4 5 6 7 ] Array after updating element at index 5. Array : [ 0 1 2 3 4 10 6 7 ] Data at index 5: 10 4 Found at index 4
C語言資料結構與演算法 - 連結串列
概述
連結串列是一系列包含項的連結。每個連結都包含與另一個連結的連線。連結串列是繼陣列之後第二常用的資料結構。以下是理解連結串列概念的重要術語。
連結 - 連結串列的每個連結都可以儲存稱為元素的資料。
Next - 連結串列的每個連結都包含指向下一個連結的連結,稱為 Next。
連結串列 - 連結串列包含指向第一個連結的連線連結,稱為 First。
連結串列表示

根據上圖所示,以下是需要考慮的重要幾點。
連結串列包含一個稱為 first 的連結元素。
每個連結都包含一個或多個數據欄位和一個稱為 next 的連結欄位。
每個連結都使用其 next 連結與其下一個連結連結。
最後一個連結包含一個值為 null 的連結,用於標記列表的結尾。
連結串列型別
以下是連結串列的各種型別。
單鏈表 - 專案導航僅向前。
雙向連結串列 - 專案可以向前和向後導航。
迴圈連結串列 - 最後一項包含指向第一個元素的 next 連結,而第一個元素包含指向最後一項的 prev 連結。
基本操作
以下是列表支援的基本操作。
插入 - 在列表開頭新增元素。
刪除 - 刪除列表開頭的元素。
顯示 - 顯示完整列表。
搜尋 - 使用給定鍵搜尋元素。
刪除 - 使用給定鍵刪除元素。
插入操作
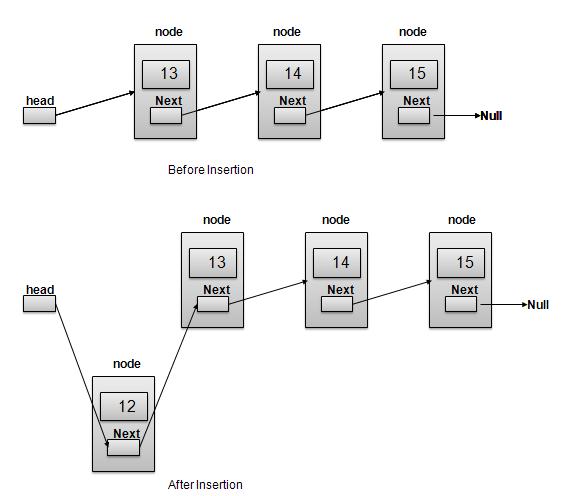
插入是一個三步過程:
使用提供的資料建立一個新的連結。
將新連結指向舊的 First 連結。
將 First 連結指向此新連結。
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
刪除操作
刪除是一個兩步過程:
獲取 First 連結指向的連結作為 Temp 連結。
將 First 連結指向 Temp 連結的 Next 連結。

//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
導航操作
導航是一個遞迴步驟過程,是許多操作(如搜尋、刪除等)的基礎:
獲取 First 連結指向的連結作為 Current 連結。
檢查 Current 連結是否不為空,並顯示它。
將 Current 連結指向 Current 連結的 Next 連結,並移動到上述步驟。

注意:
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
while(ptr != NULL){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
高階操作
以下是為列表指定的高階操作。
排序 - 基於特定順序對列表進行排序。
反轉 - 反轉連結串列。
排序操作
我們使用氣泡排序來排序列表。
void sort(){
int i, j, k, tempKey, tempData ;
struct node *current;
struct node *next;
int size = length();
k = size ;
for ( i = 0 ; i < size - 1 ; i++, k-- ) {
current = head ;
next = head->next ;
for ( j = 1 ; j < k ; j++ ) {
if ( current->data > next->data ) {
tempData = current->data ;
current->data = next->data;
next->data = tempData ;
tempKey = current->key;
current->key = next->key;
next->key = tempKey;
}
current = current->next;
next = next->next;
}
}
}
反轉操作
以下程式碼演示了反轉單鏈表。
void reverse(struct node** head_ref) {
struct node* prev = NULL;
struct node* current = *head_ref;
struct node* next;
while (current != NULL) {
next = current->next;
current->next = prev;
prev = current;
current = next;
}
*head_ref = prev;
}
示例
LinkedListDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
while(ptr != NULL){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//is list empty
bool isEmpty(){
return head == NULL;
}
int length(){
int length = 0;
struct node *current;
for(current = head; current!=NULL;
current = current->next){
length++;
}
return length;
}
//find a link with given key
struct node* find(int key){
//start from the first link
struct node* current = head;
//if list is empty
if(head == NULL){
return NULL;
}
//navigate through list
while(current->key != key){
//if it is last node
if(current->next == NULL){
return NULL;
} else {
//go to next link
current = current->next;
}
}
//if data found, return the current Link
return current;
}
//delete a link with given key
struct node* delete(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL){
return NULL;
}
//navigate through list
while(current->key != key){
//if it is last node
if(current->next == NULL){
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
previous->next = current->next;
}
return current;
}
void sort(){
int i, j, k, tempKey, tempData ;
struct node *current;
struct node *next;
int size = length();
k = size ;
for ( i = 0 ; i < size - 1 ; i++, k-- ) {
current = head ;
next = head->next ;
for ( j = 1 ; j < k ; j++ ) {
if ( current->data > next->data ) {
tempData = current->data ;
current->data = next->data;
next->data = tempData ;
tempKey = current->key;
current->key = next->key;
next->key = tempKey;
}
current = current->next;
next = next->next;
}
}
}
void reverse(struct node** head_ref) {
struct node* prev = NULL;
struct node* current = *head_ref;
struct node* next;
while (current != NULL) {
next = current->next;
current->next = prev;
prev = current;
current = next;
}
*head_ref = prev;
}
main() {
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Original List: ");
//print list
printList();
while(!isEmpty()){
struct node *temp = deleteFirst();
printf("\nDeleted value:");
printf("(%d,%d) ",temp->key,temp->data);
}
printf("\nList after deleting all items: ");
printList();
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nRestored List: ");
printList();
printf("\n");
struct node *foundLink = find(4);
if(foundLink != NULL){
printf("Element found: ");
printf("(%d,%d) ",foundLink->key,foundLink->data);
printf("\n");
} else {
printf("Element not found.");
}
delete(4);
printf("List after deleting an item: ");
printList();
printf("\n");
foundLink = find(4);
if(foundLink != NULL){
printf("Element found: ");
printf("(%d,%d) ",foundLink->key,foundLink->data);
printf("\n");
} else {
printf("Element not found.");
}
printf("\n");
sort();
printf("List after sorting the data: ");
printList();
reverse(&head);
printf("\nList after reversing the data: ");
printList();
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ] Restored List: [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] Element found: (4,1) List after deleting an item: [ (6,56) (5,40) (3,30) (2,20) (1,10) ] Element not found. List after sorting the data: [ (1,10) (2,20) (3,30) (5,40) (6,56) ] List after reversing the data: [ (6,56) (5,40) (3,30) (2,20) (1,10) ]
C語言資料結構與演算法 - 雙向連結串列
概述
雙向連結串列是連結串列的一種變體,與單鏈表相比,它可以很容易地向前和向後兩種方式進行導航。以下是理解雙向連結串列概念的重要術語。
連結 - 連結串列的每個連結都可以儲存稱為元素的資料。
Next - 連結串列的每個連結都包含指向下一個連結的連結,稱為 Next。
Prev - 連結串列的每個連結都包含指向先前連結的連結,稱為 Prev。
連結串列 - 連結串列包含指向第一個連結的連線連結(稱為 First)和指向最後一個連結的連結(稱為 Last)。
雙向連結串列表示

根據上圖所示,以下是需要考慮的重要幾點。
雙向連結串列包含一個稱為 first 和 last 的連結元素。
每個連結都包含一個或多個數據欄位和一個稱為 next 的連結欄位。
每個連結都使用其 next 連結與其下一個連結連結。
每個連結都使用其 prev 連結與其先前的連結連結。
最後一個連結包含一個值為 null 的連結,用於標記列表的結尾。
基本操作
以下是列表支援的基本操作。
插入 - 在列表開頭新增元素。
刪除 - 刪除列表開頭的元素。
插入末尾 - 在列表末尾新增元素。
刪除末尾 - 刪除列表末尾的元素。
插入到…之後 - 在列表的某個項之後新增元素。
刪除 - 使用鍵從列表中刪除元素。
向前顯示 - 以向前的方式顯示完整列表。
向後顯示 - 以向後的方式顯示完整列表。
插入操作
以下程式碼演示了在雙向連結串列開頭進行插入操作。
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()){
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
刪除操作
以下程式碼演示了在雙向連結串列開頭進行刪除操作。
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL){
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
在末尾插入操作
以下程式碼演示了在雙向連結串列的最後一個位置進行插入操作。
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()){
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
示例
DoublyLinkedListDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
struct node *prev;
};
//this link always point to first Link
struct node *head = NULL;
//this link always point to last Link
struct node *last = NULL;
struct node *current = NULL;
//is list empty
bool isEmpty(){
return head == NULL;
}
int length(){
int length = 0;
struct node *current;
for(current = head; current!=NULL;
current = current->next){
length++;
}
return length;
}
//display the list in from first to last
void displayForward(){
//start from the beginning
struct node *ptr = head;
//navigate till the end of the list
printf("\n[ ");
while(ptr != NULL){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
printf(" ]");
}
//display the list from last to first
void displayBackward(){
//start from the last
struct node *ptr = last;
//navigate till the start of the list
printf("\n[ ");
while(ptr != NULL){
//print data
printf("(%d,%d) ",ptr->key,ptr->data);
//move to next item
ptr = ptr ->prev;
printf(" ");
}
printf(" ]");
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()){
//make it the last link
last = link;
} else {
//update first prev link
head->prev = link;
}
//point it to old first link
link->next = head;
//point first to new first link
head = link;
}
//insert link at the last location
void insertLast(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key = key;
link->data = data;
if(isEmpty()){
//make it the last link
last = link;
} else {
//make link a new last link
last->next = link;
//mark old last node as prev of new link
link->prev = last;
}
//point last to new last node
last = link;
}
//delete first item
struct node* deleteFirst(){
//save reference to first link
struct node *tempLink = head;
//if only one link
if(head->next == NULL){
last = NULL;
} else {
head->next->prev = NULL;
}
head = head->next;
//return the deleted link
return tempLink;
}
//delete link at the last location
struct node* deleteLast(){
//save reference to last link
struct node *tempLink = last;
//if only one link
if(head->next == NULL){
head = NULL;
} else {
last->prev->next = NULL;
}
last = last->prev;
//return the deleted link
return tempLink;
}
//delete a link with given key
struct node* delete(int key){
//start from the first link
struct node* current = head;
struct node* previous = NULL;
//if list is empty
if(head == NULL){
return NULL;
}
//navigate through list
while(current->key != key){
//if it is last node
if(current->next == NULL){
return NULL;
} else {
//store reference to current link
previous = current;
//move to next link
current = current->next;
}
}
//found a match, update the link
if(current == head) {
//change first to point to next link
head = head->next;
} else {
//bypass the current link
current->prev->next = current->next;
}
if(current == last){
//change last to point to prev link
last = current->prev;
} else {
current->next->prev = current->prev;
}
return current;
}
bool insertAfter(int key, int newKey, int data){
//start from the first link
struct node *current = head;
//if list is empty
if(head == NULL){
return false;
}
//navigate through list
while(current->key != key){
//if it is last node
if(current->next == NULL){
return false;
} else {
//move to next link
current = current->next;
}
}
//create a link
struct node *newLink = (struct node*) malloc(sizeof(struct node));
newLink->key = key;
newLink->data = data;
if(current==last) {
newLink->next = NULL;
last = newLink;
} else {
newLink->next = current->next;
current->next->prev = newLink;
}
newLink->prev = current;
current->next = newLink;
return true;
}
main() {
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("\nList (First to Last): ");
displayForward();
printf("\n");
printf("\nList (Last to first): ");
displayBackward();
printf("\nList , after deleting first record: ");
deleteFirst();
displayForward();
printf("\nList , after deleting last record: ");
deleteLast();
displayForward();
printf("\nList , insert after key(4) : ");
insertAfter(4,7, 13);
displayForward();
printf("\nList , after delete key(4) : ");
delete(4);
displayForward();
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
List (First to Last): [ (6,56) (5,40) (4,1) (3,30) (2,20) (1,10) ] List (Last to first): [ (1,10) (2,20) (3,30) (4,1) (5,40) (6,56) ] List , after deleting first record: [ (5,40) (4,1) (3,30) (2,20) (1,10) ] List , after deleting last record: [ (5,40) (4,1) (3,30) (2,20) ] List , insert after key(4) : [ (5,40) (4,1) (4,13) (3,30) (2,20) ] List , after delete key(4) : [ (5,40) (4,13) (3,30) (2,20) ]
C語言資料結構與演算法 - 迴圈連結串列
概述
迴圈連結串列是連結串列的一種變體,其中第一個元素指向最後一個元素,而最後一個元素指向第一個元素。單鏈表和雙向連結串列都可以製成迴圈連結串列。
單鏈表作為迴圈連結串列

雙向連結串列作為迴圈連結串列

根據上圖所示,以下是需要考慮的重要幾點。
在單鏈表和雙向連結串列的兩種情況下,最後一個連結的 next 都指向列表的第一個連結。
對於雙向連結串列,第一個連結的 prev 指向列表的最後一個連結。
基本操作
以下是迴圈列表支援的重要操作。
插入 - 在列表開頭插入元素。
刪除 - 從列表開頭刪除元素。
顯示 - 顯示列表。
長度操作
以下程式碼演示了基於單鏈表在迴圈連結串列中進行插入操作。
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key =key;
link->data=data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
刪除操作
以下程式碼演示了基於單鏈表在迴圈連結串列中進行刪除操作。
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head){
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
顯示列表操作
以下程式碼演示了在迴圈連結串列中顯示列表操作。
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL){
while(ptr->next != ptr){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
示例
DoublyLinkedListDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
int key;
struct node *next;
};
struct node *head = NULL;
struct node *current = NULL;
bool isEmpty(){
return head == NULL;
}
int length(){
int length = 0;
//if list is empty
if(head == NULL){
return 0;
}
current = head->next;
while(current != head){
length++;
current = current->next;
}
return length;
}
//insert link at the first location
void insertFirst(int key, int data){
//create a link
struct node *link = (struct node*) malloc(sizeof(struct node));
link->key =key;
link->data=data;
if (isEmpty()) {
head = link;
head->next = head;
} else {
//point it to old first node
link->next = head;
//point first to new first node
head = link;
}
}
//delete first item
struct node * deleteFirst(){
//save reference to first link
struct node *tempLink = head;
if(head->next == head){
head = NULL;
return tempLink;
}
//mark next to first link as first
head = head->next;
//return the deleted link
return tempLink;
}
//display the list
void printList(){
struct node *ptr = head;
printf("\n[ ");
//start from the beginning
if(head != NULL){
while(ptr->next != ptr){
printf("(%d,%d) ",ptr->key,ptr->data);
ptr = ptr->next;
}
}
printf(" ]");
}
main() {
insertFirst(1,10);
insertFirst(2,20);
insertFirst(3,30);
insertFirst(4,1);
insertFirst(5,40);
insertFirst(6,56);
printf("Original List: ");
//print list
printList();
while(!isEmpty()){
struct node *temp = deleteFirst();
printf("\nDeleted value:");
printf("(%d,%d) ",temp->key,temp->data);
}
printf("\nList after deleting all items: ");
printList();
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Original List: [ (6,56) (5,40) (4,1) (3,30) (2,20) ] Deleted value:(6,56) Deleted value:(5,40) Deleted value:(4,1) Deleted value:(3,30) Deleted value:(2,20) Deleted value:(1,10) List after deleting all items: [ ]
C語言資料結構與演算法 - 棧
概述
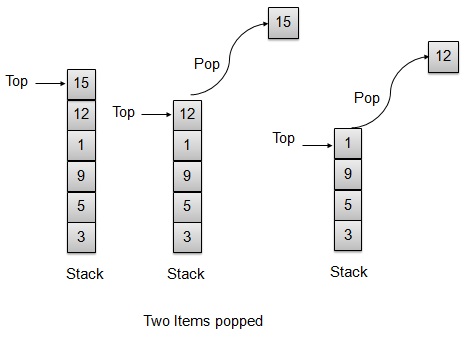
棧是一種資料結構,它只允許在一端對資料進行操作。它只允許訪問最後插入的資料。棧也被稱為 LIFO(後進先出)資料結構,並且 Push 和 Pop 操作以這樣的方式相關:只有最後壓入(新增到棧中)的專案才能彈出(從棧中移除)。
棧表示
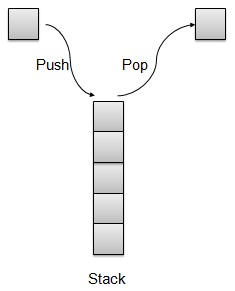
我們將在本文中使用陣列來實現棧。
基本操作
以下是棧的兩個主要操作。
Push - 將元素壓入棧頂。
Pop - 從棧頂彈出元素。
棧還支援一些其他操作。
Peek - 獲取棧頂元素。
isFull - 檢查棧是否已滿。
isEmpty - 檢查棧是否為空。
Push 操作
每當將元素壓入棧中時,棧都會將該元素儲存在儲存區的頂部,並遞增頂部索引以供以後使用。如果儲存區已滿,則通常會顯示錯誤訊息。
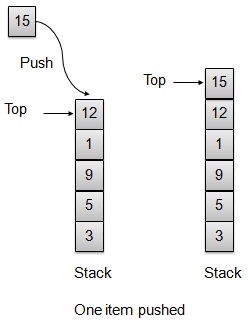
// Operation : Push
// push item on the top of the stack
void push(int data) {
if(!isFull()){
// increment top by 1 and insert data
intArray[++top] = data;
} else {
printf("Cannot add data. Stack is full.\n");
}
}
Pop 操作
每當要從棧中彈出元素時,棧都會從儲存區的頂部檢索元素,並遞減頂部索引以供以後使用。
// Operation : Pop
// pop item from the top of the stack
int pop() {
//retrieve data and decrement the top by 1
return intArray[top--];
}
示例
StackDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
// size of the stack
int size = 8;
// stack storage
int intArray[8];
// top of the stack
int top = -1;
// Operation : Pop
// pop item from the top of the stack
int pop() {
//retrieve data and decrement the top by 1
return intArray[top--];
}
// Operation : Peek
// view the data at top of the stack
int peek() {
//retrieve data from the top
return intArray[top];
}
//Operation : isFull
//return true if stack is full
bool isFull(){
return (top == size-1);
}
// Operation : isEmpty
// return true if stack is empty
bool isEmpty(){
return (top == -1);
}
// Operation : Push
// push item on the top of the stack
void push(int data) {
if(!isFull()){
// increment top by 1 and insert data
intArray[++top] = data;
} else {
printf("Cannot add data. Stack is full.\n");
}
}
main() {
// push items on to the stack
push(3);
push(5);
push(9);
push(1);
push(12);
push(15);
printf("Element at top of the stack: %d\n" ,peek());
printf("Elements: \n");
// print stack data
while(!isEmpty()){
int data = pop();
printf("%d\n",data);
}
printf("Stack full: %s\n" , isFull()?"true":"false");
printf("Stack empty: %s\n" , isEmpty()?"true":"false");
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Element at top of the stack: 15 Elements: 15 12 1 9 5 3 Stack full: false Stack empty: true
C語言資料結構與演算法 - 表示式解析
像 2*(3*4) 這樣的普通算術表示式更容易讓人理解,但對於演算法來說,解析這樣的表示式會相當困難。為了減輕這種困難,可以使用兩步法透過演算法解析算術表示式。
將提供的算術表示式轉換為字尾表示法。
計算字尾表示法。
中綴表示法
正常的算術表示式遵循中綴表示法,其中運算子位於運算元之間。例如 A+B,其中 A 是第一個運算元,B 是第二個運算元,+ 是作用於這兩個運算元的運算子。
字尾表示法
字尾表示法與正常的算術表示式或中綴表示法的區別在於,運算子位於運算元之後。例如,請考慮以下示例。
| 序號 | 中綴表示法 | 字尾表示法 |
|---|---|---|
| 1 | A+B | AB+ |
| 2 | (A+B)*C | AB+C* |
| 3 | A*(B+C) | ABC+* |
| 4 | A/B+C/D | AB/CD/+ |
| 5 | (A+B)*(C+D) | AB+CD+* |
| 6 | ((A+B)*C)-D | AB+C*D- |
中綴轉字尾轉換
在檢視將中綴轉換為字尾表示法的方法之前,我們需要考慮中綴表示式計算的基本知識。
中綴表示式的計算從左到右開始。
記住優先順序,例如 * 的優先順序高於 +。例如
2+3*4 = 2+12.
2+3*4 = 14.
-
使用括號來覆蓋優先順序,例如
(2+3)*4 = 5*4.
(2+3)*4= 20.
現在讓我們手動將簡單的中綴表示式 A+B*C 轉換為字尾表示式。
| 序號 | 讀取的字元 | 到目前為止已解析的中綴表示式 | 到目前為止已生成的逆波蘭表示式 | 備註 |
|---|---|---|---|---|
| 1 | A | A | A | |
| 2 | + | A+ | A | |
| 3 | B | A+B | AB | |
| 4 | * | A+B* | AB | 因為 * 的優先順序高於 +,所以 + 不能複製。 |
| 5 | C | A+B*C | ABC | |
| 6 | A+B*C | ABC* | 複製 *,因為有兩個運算元 B 和 C | |
| 7 | A+B*C | ABC*+ | 複製 +,因為有兩個運算元 BC 和 A |
現在讓我們使用棧將上述中綴表示式 A+B*C 轉換為字尾表示式。
| 序號 | 讀取的字元 | 到目前為止已解析的中綴表示式 | 到目前為止已生成的逆波蘭表示式 | 棧內容 | 備註 |
|---|---|---|---|---|---|
| 1 | A | A | A | ||
| 2 | + | A+ | A | + | 將 + 運算子壓入棧中。 |
| 3 | B | A+B | AB | + | |
| 4 | * | A+B* | AB | +* | * 運算子的優先順序高於 +。將 * 運算子壓入棧中。否則,+ 將彈出。 |
| 5 | C | A+B*C | ABC | +* | |
| 6 | A+B*C | ABC* | + | 沒有更多運算元,彈出 * 運算子。 | |
| 7 | A+B*C | ABC*+ | 彈出 + 運算子。 |
現在讓我們看另一個例子,使用棧將中綴表示式 A*(B+C) 轉換為字尾表示式。
| 序號 | 讀取的字元 | 到目前為止已解析的中綴表示式 | 到目前為止已生成的逆波蘭表示式 | 棧內容 | 備註 |
|---|---|---|---|---|---|
| 1 | A | A | A | ||
| 2 | * | A* | A | * | 將 * 運算子壓入棧中。 |
| 3 | ( | A*( | A | *( | 將 ( 壓入棧中。 |
| 4 | B | A*(B | AB | *( | |
| 5 | + | A*(B+ | AB | *(+ | 將 + 壓入棧中。 |
| 6 | C | A*(B+C | ABC | *(+ | |
| 7 | ) | A*(B+C) | ABC+ | *( | 彈出 + 運算子。 |
| 8 | A*(B+C) | ABC+ | * | 彈出 ( 運算子。 | |
| 9 | A*(B+C) | ABC+* | 彈出其餘的運算子。 |
示例
現在我們將演示使用棧將中綴表示式轉換為字尾表示式,然後計算字尾表示式的值。
#include<stdio.h>
#include<string.h>
//char stack
char stack[25];
int top=-1;
void push(char item) {
stack[++top]=item;
}
char pop() {
return stack[top--];
}
//returns precedence of operators
int precedence(char symbol) {
switch(symbol) {
case '+':
case '-':
return 2;
break;
case '*':
case '/':
return 3;
break;
case '^':
return 4;
break;
case '(':
case ')':
case '#':
return 1;
break;
}
}
//check whether the symbol is operator?
int isOperator(char symbol) {
switch(symbol){
case '+':
case '-':
case '*':
case '/':
case '^':
case '(':
case ')':
return 1;
break;
default:
return 0;
}
}
//converts infix expression to postfix
void convert(char infix[],char postfix[]){
int i,symbol,j=0;
stack[++top]='#';
for(i=0;i<strlen(infix);i++){
symbol=infix[i];
if(isOperator(symbol)==0){
postfix[j]=symbol;
j++;
} else {
if(symbol=='('){
push(symbol);
} else {
if(symbol==')'){
while(stack[top]!='('){
postfix[j]=pop();
j++;
}
pop();//pop out (.
} else {
if(precedence(symbol)>precedence(stack[top])) {
push(symbol);
} else {
while(precedence(symbol)<=precedence(stack[top])) {
postfix[j]=pop();
j++;
}
push(symbol);
}
}
}
}
}
while(stack[top]!='#') {
postfix[j]=pop();
j++;
}
postfix[j]='\0';//null terminate string.
}
//int stack
int stack_int[25];
int top_int=-1;
void push_int(int item) {
stack_int[++top_int]=item;
}
char pop_int() {
return stack_int[top_int--];
}
//evaluates postfix expression
int evaluate(char *postfix){
char ch;
int i=0,operand1,operand2;
while( (ch=postfix[i++]) != '\0') {
if(isdigit(ch)){
push_int(ch-'0'); // Push the operand
} else {
//Operator,pop two operands
operand2=pop_int();
operand1=pop_int();
switch(ch) {
case '+':
push_int(operand1+operand2);
break;
case '-':
push_int(operand1-operand2);
break;
case '*':
push_int(operand1*operand2);
break;
case '/':
push_int(operand1/operand2);
break;
}
}
}
return stack_int[top_int];
}
void main() {
char infix[25] = "1*(2+3)",postfix[25];
convert(infix,postfix);
printf("Infix expression is: %s\n" , infix);
printf("Postfix expression is: %s\n" , postfix);
printf("Evaluated expression is: %d\n" , evaluate(postfix));
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Infix expression is: 1*(2+3) Postfix expression is: 123+* Result is: 5
C語言資料結構與演算法 - 佇列
概述
佇列是一種類似於棧的資料結構,主要區別在於第一個插入的項是第一個被移除的項(FIFO - 先進先出),而棧是基於 LIFO(後進先出)原則的。
隊列表示
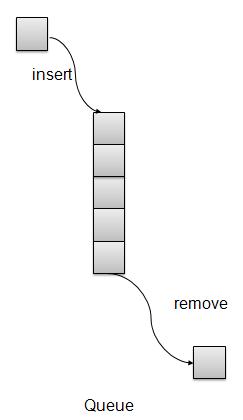
基本操作
插入/入隊 − 將一個項新增到佇列的尾部。
移除/出隊 − 從佇列的頭部移除一個項。
在本文中,我們將使用陣列實現佇列。佇列還支援一些其他操作,如下所示。
Peek − 獲取佇列頭部元素。
isFull − 檢查佇列是否已滿。
isEmpty − 檢查佇列是否為空。
插入/入隊操作
每當一個元素插入到佇列中時,佇列都會遞增尾部索引以備後用,並將該元素儲存在儲存區的尾部。如果尾部到達最後一個索引,則將其環繞到底部位置。這種安排稱為環繞,這種佇列稱為迴圈佇列。此方法也稱為入隊操作。

void insert(int data){
if(!isFull()){
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
移除/出隊操作
每當要從佇列中移除一個元素時,佇列都會使用頭部索引獲取元素並遞增頭部索引。作為環繞安排,如果頭部索引大於陣列的最大索引,則將其設定為 0。

int removeData(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
示例
QueueDemo.c
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int front = 0;
int rear = -1;
int itemCount = 0;
int peek(){
return intArray[front];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
if(!isFull()){
if(rear == MAX-1){
rear = -1;
}
intArray[++rear] = data;
itemCount++;
}
}
int removeData(){
int data = intArray[front++];
if(front == MAX){
front = 0;
}
itemCount--;
return data;
}
int main() {
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// front : 0
// rear : 4
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 3 5 9 1 12
insert(15);
// front : 0
// rear : 5
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 3 5 9 1 12 15
if(isFull()){
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// front : 1
// rear : 5
// -------------------
// index : 1 2 3 4 5
// -------------------
// queue : 5 9 1 12 15
// insert more items
insert(16);
// front : 1
// rear : -1
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 5 9 1 12 15
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()){
int n = removeData();
printf("%d ",n);
}
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Queue is full! Element removed: 3 Element at front: 5 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 5 9 1 12 15 16
C語言資料結構與演算法 - 優先佇列
概述
優先佇列比佇列更專業的資料結構。與普通佇列一樣,優先佇列具有相同的方法,但有一個主要區別。在優先佇列中,項按鍵值排序,以便鍵值最低的項位於前面,鍵值最高的項位於後面,反之亦然。因此,我們根據項的鍵值分配優先順序。值越低,優先順序越高。以下是優先佇列的主要方法。
基本操作
插入/入隊 − 將一個項新增到佇列的尾部。
移除/出隊 − 從佇列的頭部移除一個項。
優先隊列表示

在本文中,我們將使用陣列實現佇列。佇列還支援一些其他操作,如下所示。
Peek − 獲取佇列頭部元素。
isFull − 檢查佇列是否已滿。
isEmpty − 檢查佇列是否為空。
插入/入隊操作
每當將元素插入佇列時,優先佇列會根據其順序插入該項。這裡我們假設資料值越高,優先順序越低。

void insert(int data){
int i =0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
} else {
// start from the right end of the queue
for(i = itemCount - 1; i >= 0; i-- ){
// if data is larger, shift existing item to right end
if(data > intArray[i]){
intArray[i+1] = intArray[i];
} else {
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
移除/出隊操作
每當要從佇列中移除一個元素時,佇列會使用專案計數獲取該元素。一旦元素被移除,專案計數就會減少一個。

int removeData(){
return intArray[--itemCount];
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 6
int intArray[MAX];
int itemCount = 0;
int peek(){
return intArray[itemCount - 1];
}
bool isEmpty(){
return itemCount == 0;
}
bool isFull(){
return itemCount == MAX;
}
int size(){
return itemCount;
}
void insert(int data){
int i =0;
if(!isFull()){
// if queue is empty, insert the data
if(itemCount == 0){
intArray[itemCount++] = data;
} else {
// start from the right end of the queue
for(i = itemCount - 1; i >= 0; i-- ){
// if data is larger, shift existing item to right end
if(data > intArray[i]){
intArray[i+1] = intArray[i];
} else {
break;
}
}
// insert the data
intArray[i+1] = data;
itemCount++;
}
}
}
int removeData(){
return intArray[--itemCount];
}
int main() {
/* insert 5 items */
insert(3);
insert(5);
insert(9);
insert(1);
insert(12);
// ------------------
// index : 0 1 2 3 4
// ------------------
// queue : 12 9 5 3 1
insert(15);
// ---------------------
// index : 0 1 2 3 4 5
// ---------------------
// queue : 15 12 9 5 3 1
if(isFull()){
printf("Queue is full!\n");
}
// remove one item
int num = removeData();
printf("Element removed: %d\n",num);
// ---------------------
// index : 0 1 2 3 4
// ---------------------
// queue : 15 12 9 5 3
// insert more items
insert(16);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
// As queue is full, elements will not be inserted.
insert(17);
insert(18);
// ----------------------
// index : 0 1 2 3 4 5
// ----------------------
// queue : 16 15 12 9 5 3
printf("Element at front: %d\n",peek());
printf("----------------------\n");
printf("index : 5 4 3 2 1 0\n");
printf("----------------------\n");
printf("Queue: ");
while(!isEmpty()){
int n = removeData();
printf("%d ",n);
}
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Queue is full! Element removed: 1 Element at front: 3 ---------------------- index : 5 4 3 2 1 0 ---------------------- Queue: 3 5 9 12 15 16
C語言資料結構與演算法 - 樹
概述
樹表示由邊連線的節點。我們將專門討論二叉樹或二叉搜尋樹。
二叉樹是一種用於資料儲存的特殊資料結構。二叉樹有一個特殊條件,即每個節點最多可以有兩個子節點。二叉樹兼具有序陣列和連結串列的優點,搜尋速度與排序陣列一樣快,插入或刪除操作速度與連結串列一樣快。
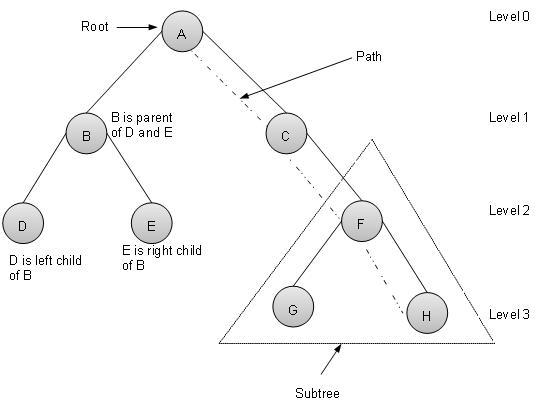
術語
以下是關於樹的一些重要術語。
路徑 − 路徑是指沿著樹的邊的節點序列。
根 − 樹頂部的節點稱為根。每棵樹只有一個根,並且從根節點到任何節點只有一條路徑。
父節點 − 除根節點外的任何節點都有一條向上指向稱為父節點的節點的邊。
子節點 − 透過其向下邊連線到給定節點下方的節點稱為其子節點。
葉子節點 − 沒有子節點的節點稱為葉子節點。
子樹 − 子樹表示節點的後代。
訪問 − 訪問是指當控制處於節點上時檢查節點的值。
遍歷 − 遍歷意味著以特定順序透過節點。
層級 − 節點的層級表示節點的代數。如果根節點位於第 0 層,則其下一個子節點位於第 1 層,其孫子節點位於第 2 層,依此類推。
鍵 − 鍵表示節點的值,基於此值將對節點執行搜尋操作。
二叉搜尋樹表現出一種特殊行為。節點的左子節點的值必須小於其父節點的值,節點的右子節點的值必須大於其父節點的值。
二叉搜尋樹表示
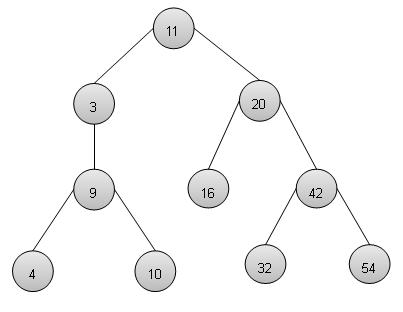
我們將使用節點物件實現樹,並透過引用將它們連線起來。
基本操作
以下是樹的基本主要操作:
搜尋 − 在樹中搜索元素。
插入 − 在樹中插入元素。
先序遍歷 − 以先序方式遍歷樹。
中序遍歷 − 以中序方式遍歷樹。
後序遍歷 − 以後序方式遍歷樹。
節點
定義一個節點,它包含一些資料以及對其左右子節點的引用。
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
搜尋操作
每當要搜尋元素時,從根節點開始搜尋,如果資料小於鍵值,則在左子樹中搜索元素,否則在右子樹中搜索元素。對每個節點遵循相同的演算法。
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}//else go to right tree
else{
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
return current;
}
插入操作
每當要插入元素時,首先找到其適當的位置。從根節點開始搜尋,如果資料小於鍵值,則在左子樹中搜索空位置並插入資料。否則,在右子樹中搜索空位置並插入資料。
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL){
root = tempNode;
} else {
current = root;
parent = NULL;
while(1){
parent = current;
//go to left of the tree
if(data < parent->data){
current = current->leftChild;
//insert to the left
if(current == NULL){
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current->rightChild;
//insert to the right
if(current == NULL){
parent->rightChild = tempNode;
return;
}
}
}
}
}
先序遍歷
這是一個簡單的三步過程。
訪問根節點
遍歷左子樹
遍歷右子樹
void preOrder(struct node* root){
if(root!=NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}
中序遍歷
這是一個簡單的三步過程。
遍歷左子樹
訪問根節點
遍歷右子樹
void inOrder(struct node* root){
if(root!=NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}
後序遍歷
這是一個簡單的三步過程。
遍歷左子樹
遍歷右子樹
訪問根節點
void postOrder(struct node* root){
if(root!=NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
struct node {
int data;
struct node *leftChild;
struct node *rightChild;
};
struct node *root = NULL;
void insert(int data){
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
struct node *current;
struct node *parent;
tempNode->data = data;
tempNode->leftChild = NULL;
tempNode->rightChild = NULL;
//if tree is empty
if(root == NULL){
root = tempNode;
} else {
current = root;
parent = NULL;
while(1){
parent = current;
//go to left of the tree
if(data < parent->data){
current = current->leftChild;
//insert to the left
if(current == NULL){
parent->leftChild = tempNode;
return;
}
}//go to right of the tree
else{
current = current->rightChild;
//insert to the right
if(current == NULL){
parent->rightChild = tempNode;
return;
}
}
}
}
}
struct node* search(int data){
struct node *current = root;
printf("Visiting elements: ");
while(current->data != data){
if(current != NULL)
printf("%d ",current->data);
//go to left tree
if(current->data > data){
current = current->leftChild;
}//else go to right tree
else{
current = current->rightChild;
}
//not found
if(current == NULL){
return NULL;
}
}
return current;
}
void preOrder(struct node* root){
if(root!=NULL){
printf("%d ",root->data);
preOrder(root->leftChild);
preOrder(root->rightChild);
}
}
void inOrder(struct node* root){
if(root!=NULL){
inOrder(root->leftChild);
printf("%d ",root->data);
inOrder(root->rightChild);
}
}
void postOrder(struct node* root){
if(root!=NULL){
postOrder(root->leftChild);
postOrder(root->rightChild);
printf("%d ",root->data);
}
}
void traverse(int traversalType){
switch(traversalType){
case 1:
printf("\nPreorder traversal: ");
preOrder(root);
break;
case 2:
printf("\nInorder traversal: ");
inOrder(root);
break;
case 3:
printf("\nPostorder traversal: ");
postOrder(root);
break;
}
}
int main()
{
/* 11 //Level 0
*/
insert(11);
/* 11 //Level 0
* |
* |---20 //Level 1
*/
insert(20);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
*/
insert(3);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
*/
insert(42);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* |--42 //Level 2
* |
* |--54 //Level 3
*/
insert(54);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* |--54 //Level 3
*/
insert(16);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* |
* 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(32);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* |
* 32--|--54 //Level 3
*/
insert(9);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--| 32--|--54 //Level 3
*/
insert(4);
/* 11 //Level 0
* |
* 3---|---20 //Level 1
* | |
* |--9 16--|--42 //Level 2
* | |
* 4--|--10 32--|--54 //Level 3
*/
insert(10);
struct node * temp = search(32);
if(temp!=NULL){
printf("Element found.\n");
printf("( %d )",temp->data);
printf("\n");
} else {
printf("Element not found.\n");
}
struct node *node1 = search(2);
if(node1!=NULL){
printf("Element found.\n");
printf("( %d )",node1->data);
printf("\n");
} else {
printf("Element not found.\n");
}
//pre-order traversal
//root, left ,right
traverse(1);
//in-order traversal
//left, root ,right
traverse(2);
//post order traversal
//left, right, root
traverse(3);
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Visiting elements: 11 20 42 Element found.(32) Visiting elements: 11 3 Element not found. Preorder traversal: 11 3 9 4 10 20 16 42 32 54 Inorder traversal: 3 4 9 10 11 16 20 32 42 54 Postorder traversal: 4 10 9 3 16 32 54 42 20 11
C語言資料結構與演算法 - 雜湊表
概述
雜湊表是一種資料結構,其中插入和搜尋操作非常快,與雜湊表的大小無關。它幾乎是常數或 O(1)。雜湊表使用陣列作為儲存介質,並使用雜湊技術生成要插入元素或從中定位元素的索引。
雜湊
雜湊是一種將一系列鍵值轉換為陣列索引範圍的技術。我們將使用模運算子來獲取一系列鍵值。考慮一個大小為 20 的雜湊表的例子,並且要儲存以下項。項採用 (鍵,值) 格式。
(1,20)
(2,70)
(42,80)
(4,25)
(12,44)
(14,32)
(17,11)
(13,78)
(37,98)
| 序號 | 鍵 | 雜湊值 | 陣列索引 |
|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 |
| 4 | 4 | 4 % 20 = 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 |
線性探測
正如我們所看到的,使用的方法建立的雜湊技術可能會建立陣列中已經使用的索引。在這種情況下,我們可以透過檢視下一個單元格直到找到一個空單元格來搜尋陣列中的下一個空位置。這種技術稱為線性探測。
| 序號 | 鍵 | 雜湊值 | 陣列索引 | 線性探測後,陣列索引 |
|---|---|---|---|---|
| 1 | 1 | 1 % 20 = 1 | 1 | 1 |
| 2 | 2 | 2 % 20 = 2 | 2 | 2 |
| 3 | 42 | 42 % 20 = 2 | 2 | 3 |
| 4 | 4 | 4 % 20 = 4 | 4 | 4 |
| 5 | 12 | 12 % 20 = 12 | 12 | 12 |
| 6 | 14 | 14 % 20 = 14 | 14 | 14 |
| 7 | 17 | 17 % 20 = 17 | 17 | 17 |
| 8 | 13 | 13 % 20 = 13 | 13 | 13 |
| 9 | 37 | 37 % 20 = 17 | 17 | 18 |
基本操作
以下是雜湊表的基本主要操作:
搜尋 − 在雜湊表中搜索元素。
插入 − 在雜湊表中插入元素。
刪除 − 從雜湊表中刪除元素。
資料項
定義一個數據項,它包含一些資料和鍵,基於該鍵在雜湊表中進行搜尋。
struct DataItem {
int data;
int key;
};
雜湊方法
定義一個雜湊方法來計算資料項鍵的雜湊碼。
int hashCode(int key){
return key % SIZE;
}
搜尋操作
每當要搜尋元素時,計算傳遞的鍵的雜湊碼,並使用該雜湊碼作為陣列中的索引來定位元素。如果在計算的雜湊碼處找不到元素,則使用線性探測來獲取前方的元素。
struct DataItem *search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL){
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
插入操作
每當要插入元素時,計算傳遞的鍵的雜湊碼,並使用該雜湊碼作為陣列中的索引來定位索引。如果在計算的雜湊碼處找到元素,則使用線性探測查詢空位置。
void insert(int key,int data){
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] !=NULL &&
hashArray[hashIndex]->key != -1){
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
刪除操作
每當要刪除元素時,計算傳遞的鍵的雜湊碼,並使用該雜湊碼作為陣列中的索引來定位索引。如果在計算的雜湊碼處找不到元素,則使用線性探測來獲取前方的元素。找到後,在那裡儲存一個虛擬項以保持雜湊表的效能不變。
struct DataItem* delete(struct DataItem* item){
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL){
if(hashArray[hashIndex]->key == key){
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define SIZE 20
struct DataItem {
int data;
int key;
};
struct DataItem* hashArray[SIZE];
struct DataItem* dummyItem;
struct DataItem* item;
int hashCode(int key){
return key % SIZE;
}
struct DataItem *search(int key){
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL){
if(hashArray[hashIndex]->key == key)
return hashArray[hashIndex];
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void insert(int key,int data){
struct DataItem *item = (struct DataItem*) malloc(sizeof(struct DataItem));
item->data = data;
item->key = key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty or deleted cell
while(hashArray[hashIndex] !=NULL &&
hashArray[hashIndex]->key != -1){
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
hashArray[hashIndex] = item;
}
struct DataItem* delete(struct DataItem* item){
int key = item->key;
//get the hash
int hashIndex = hashCode(key);
//move in array until an empty
while(hashArray[hashIndex] !=NULL){
if(hashArray[hashIndex]->key == key){
struct DataItem* temp = hashArray[hashIndex];
//assign a dummy item at deleted position
hashArray[hashIndex] = dummyItem;
return temp;
}
//go to next cell
++hashIndex;
//wrap around the table
hashIndex %= SIZE;
}
return NULL;
}
void display(){
int i=0;
for(i=0; i<SIZE; i++) {
if(hashArray[i] != NULL)
printf(" (%d,%d)",hashArray[i]->key,hashArray[i]->data);
else
printf(" ~~ ");
}
printf("\n");
}
int main(){
dummyItem = (struct DataItem*) malloc(sizeof(struct DataItem));
dummyItem->data = -1;
dummyItem->key = -1;
insert(1, 20);
insert(2, 70);
insert(42, 80);
insert(4, 25);
insert(12, 44);
insert(14, 32);
insert(17, 11);
insert(13, 78);
insert(37, 97);
display();
item = search(37);
if(item != NULL){
printf("Element found: %d\n", item->data);
} else {
printf("Element not found\n");
}
delete(item);
item = search(37);
if(item != NULL){
printf("Element found: %d\n", item->data);
} else {
printf("Element not found\n");
}
}
如果我們編譯並執行上述程式,則它將產生以下結果:
~~ (1,20) (2,70) (42,80) (4,25) ~~ ~~ ~~ ~~ ~~ ~~ ~~ (12,44) (13,78) (14,32) ~~ ~~ (17,11) (37,97) ~~ Element found: 97 Element not found
C語言資料結構與演算法 - 堆
概述
堆表示一種特殊的基於樹的資料結構,用於表示優先佇列或用於堆排序。我們將專門討論二叉堆樹。
二叉堆樹可以分為具有兩個約束的二叉樹:
完整性 − 二叉堆樹是一個完整的二叉樹,除了最後一層可能並非所有元素都存在,但元素應該從左到右填充。
堆特性 − 所有父節點都應該大於或小於其子節點。如果父節點大於其子節點,則稱為最大堆,否則稱為最小堆。最大堆用於堆排序,最小堆用於優先佇列。我們正在考慮最小堆,並將使用陣列實現。
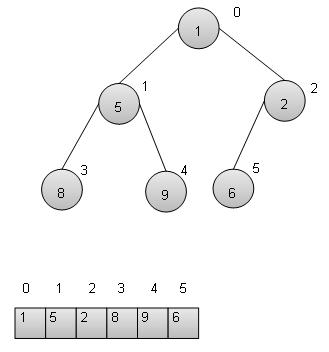
基本操作
以下是最小堆的基本主要操作:
插入 − 在堆中插入元素。
獲取最小值 − 從堆中獲取最小元素。
移除最小值 − 從堆中移除最小元素
插入操作
每當要插入元素時,將元素插入陣列的末尾。將堆的大小增加 1。
當堆屬性被破壞時,向上調整元素。將元素與其父節點的值進行比較,如果需要則交換它們。
void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
獲取最小值
獲取實現堆的陣列的第一個元素作為根。
int getMinimum(){
return intArray[0];
}
移除最小值
每當要移除元素時,獲取陣列的最後一個元素並將堆的大小減少 1。
當堆屬性被破壞時,向下調整元素。將元素與其子節點的值進行比較,如果需要則交換它們。
void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
int intArray[10];
int size;
bool isEmpty(){
return size == 0;
}
int getMinimum(){
return intArray[0];
}
int getLeftChildIndex(int nodeIndex){
return 2*nodeIndex +1;
}
int getRightChildIndex(int nodeIndex){
return 2*nodeIndex +2;
}
int getParentIndex(int nodeIndex){
return (nodeIndex -1)/2;
}
bool isFull(){
return size == 10;
}
/**
* Heap up the new element,until heap property is broken.
* Steps:
* 1. Compare node's value with parent's value.
* 2. Swap them, If they are in wrong order.
* */
void heapUp(int nodeIndex){
int parentIndex, tmp;
if (nodeIndex != 0) {
parentIndex = getParentIndex(nodeIndex);
if (intArray[parentIndex] > intArray[nodeIndex]) {
tmp = intArray[parentIndex];
intArray[parentIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapUp(parentIndex);
}
}
}
/**
* Heap down the root element being least in value,until heap property is broken.
* Steps:
* 1.If current node has no children, done.
* 2.If current node has one children and heap property is broken,
* 3.Swap the current node and child node and heap down.
* 4.If current node has one children and heap property is broken, find smaller one
* 5.Swap the current node and child node and heap down.
* */
void heapDown(int nodeIndex){
int leftChildIndex, rightChildIndex, minIndex, tmp;
leftChildIndex = getLeftChildIndex(nodeIndex);
rightChildIndex = getRightChildIndex(nodeIndex);
if (rightChildIndex >= size) {
if (leftChildIndex >= size)
return;
else
minIndex = leftChildIndex;
} else {
if (intArray[leftChildIndex] <= intArray[rightChildIndex])
minIndex = leftChildIndex;
else
minIndex = rightChildIndex;
}
if (intArray[nodeIndex] > intArray[minIndex]) {
tmp = intArray[minIndex];
intArray[minIndex] = intArray[nodeIndex];
intArray[nodeIndex] = tmp;
heapDown(minIndex);
}
}
void insert(int value) {
size++;
intArray[size - 1] = value;
heapUp(size - 1);
}
void removeMin() {
intArray[0] = intArray[size - 1];
size--;
if (size > 0)
heapDown(0);
}
main() {
/* 5 //Level 0
*
*/
insert(5);
/* 1 //Level 0
* |
* 5---| //Level 1
*/
insert(1);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
*/
insert(3);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--| //Level 2
*/
insert(8);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* |
* 8--|--9 //Level 2
*/
insert(9);
/* 1 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
insert(6);
/* 1 //Level 0
* |
* 5---|---2 //Level 1
* | |
* 8--|--9 6--|--3 //Level 2
*/
insert(2);
printf("%d", getMinimum());
removeMin();
/* 2 //Level 0
* |
* 5---|---3 //Level 1
* | |
* 8--|--9 6--| //Level 2
*/
printf("\n%d", getMinimum());
}
如果我們編譯並執行上述程式,則它將產生以下結果:
1 2
C語言資料結構與演算法 - 圖
概述
圖是一種資料結構,用於模擬數學圖。它由一組稱為頂點的邊的連線對組成。我們可以使用頂點陣列和二維邊陣列來表示圖。
重要術語
頂點 − 圖的每個節點都表示為一個頂點。在下面的示例中,標記的圓圈表示頂點。因此 A 到 G 是頂點。我們可以使用陣列來表示它們,如下面的影像所示。這裡 A 可以用索引 0 標識。B 可以用索引 1 標識,依此類推。
邊 − 邊表示兩個頂點之間的路徑或兩點之間的線。在下面的示例中,從 A 到 B、B 到 C 等等的線表示邊。我們可以使用二維陣列來表示陣列,如下面的影像所示。這裡 AB 可以用第 0 行第 1 列的 1 表示,BC 可以用第 1 行第 2 列的 1 表示,依此類推,其他組合保持為 0。
鄰接 − 如果兩個節點或頂點透過一條邊相互連線,則它們是鄰接的。在下面的示例中,B 與 A 鄰接,C 與 B 鄰接,依此類推。
路徑 − 路徑表示兩個頂點之間的一系列邊。在下面的示例中,ABCD 表示從 A 到 D 的路徑。
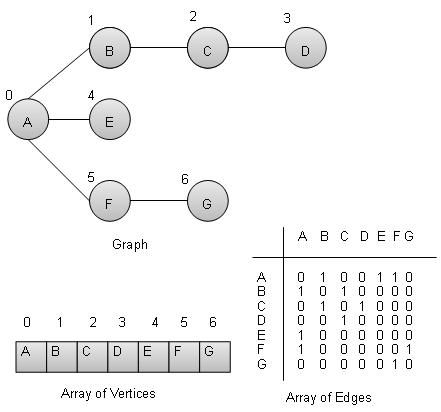
基本操作
以下是圖的基本主要操作:
新增頂點 − 向圖中新增一個頂點。
新增邊 − 在圖的兩個頂點之間新增一條邊。
顯示頂點 − 顯示圖中的一個頂點。
新增頂點操作
//add vertex to the vertex list
void addVertex(char label){
struct vertex* vertex =
(struct vertex*) malloc(sizeof(struct vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
新增邊操作
//add edge to edge array
void addEdge(int start,int end){
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
顯示邊操作
//display the vertex
void displayVertex(int vertexIndex){
printf("%c ",lstVertices[vertexIndex]->label);
}
遍歷演算法
以下是圖中重要的遍歷演算法。
深度優先搜尋 − 深度優先遍歷圖。
廣度優先搜尋 − 廣度優先遍歷圖。
深度優先搜尋演算法
深度優先搜尋演算法 (DFS) 以深度優先的方式遍歷圖,並使用堆疊來記住當任何迭代中出現死衚衕時要開始搜尋的下一個頂點。
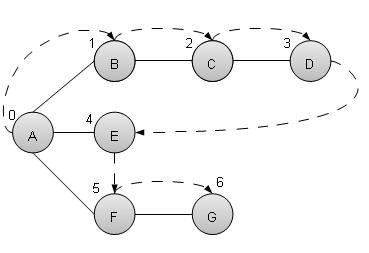
如上例所示,DFS 演算法首先從 A 遍歷到 B、C、D,然後到 E,然後到 F,最後到 G。它採用以下規則。
規則 1 − 訪問相鄰的未訪問頂點。標記為已訪問。顯示它。將其壓入堆疊。
規則 2 − 如果找不到相鄰頂點,則從堆疊中彈出頂點。(它將彈出堆疊中所有沒有相鄰頂點的頂點。)
規則 3 − 重複規則 1 和規則 2,直到堆疊為空。
void depthFirstSearch(){
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
push(0);
while(!isStackEmpty()){
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(peek());
//no adjacent vertex found
if(unvisitedVertex == -1){
pop();
} else {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(i=0;i < vertexCount;i++){
lstVertices[i]->visited = false;
}
}
廣度優先搜尋演算法
廣度優先搜尋演算法 (BFS) 以廣度優先的方式遍歷圖,並使用佇列來記住當任何迭代中出現死衚衕時要開始搜尋的下一個頂點。
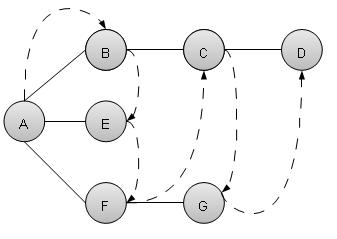
如上例所示,BFS 演算法首先從 A 遍歷到 B、E、F,然後到 C 和 G,最後到 D。它採用以下規則。
規則 1 − 訪問相鄰的未訪問頂點。標記為已訪問。顯示它。將其插入佇列。
規則 2 − 如果找不到相鄰頂點,則從佇列中移除第一個頂點。
規則 3 − 重複規則 1 和規則 2,直到佇列為空。
void breadthFirstSearch(){
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()){
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i=0;i<vertexCount;i++){
lstVertices[i]->visited = false;
}
}
示例
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>
#define MAX 10
struct Vertex {
char label;
bool visited;
};
//stack variables
int stack[MAX];
int top=-1;
//queue variables
int queue[MAX];
int rear=-1;
int front=0;
int queueItemCount = 0;
//graph variables
//array of vertices
struct Vertex* lstVertices[MAX];
//adjacency matrix
int adjMatrix[MAX][MAX];
//vertex count
int vertexCount = 0;
//stack functions
void push(int item) {
stack[++top]=item;
}
int pop() {
return stack[top--];
}
int peek() {
return stack[top];
}
bool isStackEmpty(){
return top == -1;
}
//queue functions
void insert(int data){
queue[++rear] = data;
queueItemCount++;
}
int removeData(){
queueItemCount--;
return queue[front++];
}
bool isQueueEmpty(){
return queueItemCount == 0;
}
//graph functions
//add vertex to the vertex list
void addVertex(char label){
struct Vertex* vertex = (struct Vertex*) malloc(sizeof(struct Vertex));
vertex->label = label;
vertex->visited = false;
lstVertices[vertexCount++] = vertex;
}
//add edge to edge array
void addEdge(int start,int end){
adjMatrix[start][end] = 1;
adjMatrix[end][start] = 1;
}
//display the vertex
void displayVertex(int vertexIndex){
printf("%c ",lstVertices[vertexIndex]->label);
}
//get the adjacent unvisited vertex
int getAdjUnvisitedVertex(int vertexIndex){
int i;
for(i=0; i<vertexCount; i++)
if(adjMatrix[vertexIndex][i]==1 && lstVertices[i]->visited==false)
return i;
return -1;
}
void depthFirstSearch(){
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//push vertex index in stack
push(0);
while(!isStackEmpty()){
//get the unvisited vertex of vertex which is at top of the stack
int unvisitedVertex = getAdjUnvisitedVertex(peek());
//no adjacent vertex found
if(unvisitedVertex == -1){
pop();
} else {
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
push(unvisitedVertex);
}
}
//stack is empty, search is complete, reset the visited flag
for(i=0;i < vertexCount;i++){
lstVertices[i]->visited = false;
}
}
void breadthFirstSearch(){
int i;
//mark first node as visited
lstVertices[0]->visited = true;
//display the vertex
displayVertex(0);
//insert vertex index in queue
insert(0);
int unvisitedVertex;
while(!isQueueEmpty()){
//get the unvisited vertex of vertex which is at front of the queue
int tempVertex = removeData();
//no adjacent vertex found
while((unvisitedVertex=getAdjUnvisitedVertex(tempVertex)) != -1){
lstVertices[unvisitedVertex]->visited = true;
displayVertex(unvisitedVertex);
insert(unvisitedVertex);
}
}
//queue is empty, search is complete, reset the visited flag
for(i=0;i<vertexCount;i++){
lstVertices[i]->visited = false;
}
}
main() {
int i, j;
for(i=0; i<MAX; i++) // set adjacency
for(j=0; j<MAX; j++) // matrix to 0
adjMatrix[i][j] = 0;
addVertex('A'); //0
addVertex('B'); //1
addVertex('C'); //2
addVertex('D'); //3
addVertex('E'); //4
addVertex('F'); //5
addVertex('G'); //6
/* 1 2 3
* 0 |--B--C--D
* A--|
* |
* | 4
* |-----E
* | 5 6
* | |--F--G
* |--|
*/
addEdge(0, 1); //AB
addEdge(1, 2); //BC
addEdge(2, 3); //CD
addEdge(0, 4); //AC
addEdge(0, 5); //AF
addEdge(5, 6); //FG
printf("Depth First Search: ");
//A B C D E F G
depthFirstSearch();
printf("\nBreadth First Search: ");
//A B E F C G D
breadthFirstSearch();
}
如果我們編譯並執行上述程式,則它將產生以下結果:
Depth First Search: A B C D E F G Breadth First Search: A B E F C G D
使用 C 語言的 DSA - 搜尋技術
搜尋是指在專案集合中查詢具有指定屬性的所需元素。我們將使用以下常用且簡單的搜尋演算法開始我們的討論。
| 序號 | 技術和描述 |
|---|---|
| 1 |
線性搜尋搜尋所有專案,其最壞執行時間為 n,其中 n 是專案數。 |
| 2 |
二分搜尋要求專案按排序順序排列,但其最壞執行時間是常數,並且比線性搜尋快得多。 |
| 3 |
插值搜尋要求專案按排序順序排列,但其最壞執行時間為 O(n),其中 n 是專案數,並且它比線性搜尋快得多。 |
使用 C 語言的 DSA - 排序技術
概述
排序是指以特定格式排列資料。排序演算法指定以特定順序排列資料的方式。最常見的順序是數字順序或字典順序。
排序的重要性在於,如果資料以排序方式儲存,則可以將資料搜尋最佳化到非常高的水平。排序還用於以更易讀的格式表示資料。現實生活中排序的一些示例如下。
電話簿 − 電話簿按姓名對人的電話號碼進行排序。以便可以搜尋姓名。
字典 − 字典按字母順序排列單詞,以便任何單詞的搜尋都變得容易。
排序型別
以下是流行的排序演算法及其比較列表。
| 序號 | 技術和描述 |
|---|---|
| 1 |
氣泡排序易於理解和實現,但效能非常差。 |
| 2 |
選擇排序顧名思義,使用選擇所需專案並相應準備排序陣列的技術。 |
| 3 |
插入排序是選擇排序的一種變體。 |
| 4 |
希爾排序是插入排序的有效版本。 |
| 5 |
快速排序是一種高效的排序演算法。 |
C語言資料結構與演算法 - 遞迴
概述
遞迴是指程式語言中一種函式呼叫自身的技術。呼叫自身的函式稱為遞迴方法。
特性
遞迴函式必須具有以下兩個特徵。
基本情況
一組規則,透過減少情況來導致基本情況。
遞迴階乘
階乘是遞迴的經典示例之一。階乘是一個滿足以下條件的非負數。
0! = 1
1! = 1
n! = n * (n-1)!
階乘用“!”表示。這裡規則 1 和規則 2 是基本情況,規則 3 是階乘規則。
例如,3! = 3 x 2 x 1 = 6
int factorial(int n){
//base case
if(n == 0){
return 1;
} else {
return n * factorial(n-1);
}
}

遞迴斐波那契數列
斐波那契數列是遞迴的另一個經典示例。斐波那契數列是一系列滿足以下條件的整數。
F0 = 0
F1 = 1
Fn = Fn-1 + Fn-2
斐波那契數列用“F”表示。這裡規則 1 和規則 2 是基本情況,規則 3 是斐波那契規則。
例如,F5 = 0 1 1 2 3
示例
#include <stdio.h>
int factorial(int n){
//base case
if(n == 0){
return 1;
} else {
return n * factorial(n-1);
}
}
int fibbonacci(int n){
if(n ==0){
return 0;
}
else if(n==1){
return 1;
} else {
return (fibbonacci(n-1) + fibbonacci(n-2));
}
}
main(){
int n = 5;
int i;
printf("Factorial of %d: %d\n" , n , factorial(n));
printf("Fibbonacci of %d: " , n);
for(i=0;i<n;i++){
printf("%d ",fibbonacci(i));
}
}
輸出
如果我們編譯並執行上述程式,它將產生以下輸出:
Factorial of 5: 120 Fibbonacci of 5: 0 1 1 2 3