使用 C 語言實現資料結構 - 堆

上一頁
下一頁

概述

堆表示一種特殊的基於樹的資料結構，用於表示優先佇列或用於堆排序。我們將具體討論二叉堆樹。

二叉堆樹可以歸類為具有兩個約束條件的二叉樹：

  • 完整性 - 二叉堆樹是一個完整的二叉樹，除了最後一層可能沒有所有元素，但元素應從左到右填充。

  • 堆特性 - 所有父節點都應大於或小於其子節點。如果父節點大於其子節點，則稱為最大堆，否則稱為最小堆。最大堆用於堆排序，最小堆用於優先佇列。我們正在考慮最小堆，並將使用陣列來實現它。

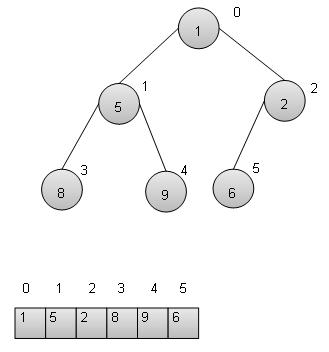
Binary Heap

基本操作

以下是最小堆的基本主要操作：

  • 插入 - 將元素插入堆中。

  • 獲取最小值 - 從堆中獲取最小元素。

  • 刪除最小值 - 從堆中刪除最小元素

插入操作

  • 每當要插入元素時。將元素插入陣列的末尾。將堆的大小增加 1。

  • 當堆屬性被破壞時，向上調整元素。將元素與其父節點的值進行比較，如果需要則交換它們。

void insert(int value) {            
   size++;
   intArray[size - 1] = value;
   heapUp(size - 1);
}
void heapUp(int nodeIndex){
   int parentIndex, tmp;
   if (nodeIndex != 0) {
      parentIndex = getParentIndex(nodeIndex);
      if (intArray[parentIndex] > intArray[nodeIndex]) {
         tmp = intArray[parentIndex];
         intArray[parentIndex] = intArray[nodeIndex];
         intArray[nodeIndex] = tmp;
         heapUp(parentIndex);
      }
   }
}

獲取最小值

獲取實現堆的陣列的第一個元素，即根節點。

int getMinimum(){
   return intArray[0];
}

刪除最小值

  • 每當要刪除元素時。獲取陣列的最後一個元素並將堆的大小減少 1。

  • 當堆屬性被破壞時，向下調整元素。將元素與其子節點的值進行比較，如果需要則交換它們。

void removeMin() {
   intArray[0] = intArray[size - 1];
   size--;
   if (size > 0)
      heapDown(0);
}
void heapDown(int nodeIndex){
   int leftChildIndex, rightChildIndex, minIndex, tmp;
   leftChildIndex = getLeftChildIndex(nodeIndex);
   rightChildIndex = getRightChildIndex(nodeIndex);
   if (rightChildIndex >= size) {
      if (leftChildIndex >= size)
         return;
      else
         minIndex = leftChildIndex;
   } else {
      if (intArray[leftChildIndex] <= intArray[rightChildIndex])
         minIndex = leftChildIndex;
      else
         minIndex = rightChildIndex;
   }
   if (intArray[nodeIndex] > intArray[minIndex]) {
      tmp = intArray[minIndex];
      intArray[minIndex] = intArray[nodeIndex];
      intArray[nodeIndex] = tmp;
      heapDown(minIndex);
   }
}

示例

線上演示 
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <stdbool.h>

int intArray[10];
int size;

bool isEmpty(){
   return size == 0;
}
int getMinimum(){
   return intArray[0];
}
int getLeftChildIndex(int nodeIndex){
   return 2*nodeIndex +1;
}
int getRightChildIndex(int nodeIndex){
   return 2*nodeIndex +2;
}
int getParentIndex(int nodeIndex){
   return (nodeIndex -1)/2;
}
bool isFull(){
   return size == 10;
}
/**
* Heap up the new element,until heap property is broken. 
* Steps:
* 1. Compare node's value with parent's value. 
* 2. Swap them, If they are in wrong order.
* */
void heapUp(int nodeIndex){
   int parentIndex, tmp;
   if (nodeIndex != 0) {
      parentIndex = getParentIndex(nodeIndex);
      if (intArray[parentIndex] > intArray[nodeIndex]) {
         tmp = intArray[parentIndex];
         intArray[parentIndex] = intArray[nodeIndex];
         intArray[nodeIndex] = tmp;
         heapUp(parentIndex);
      }
   }
}
/**
* Heap down the root element being least in value,until heap property is broken. 
* Steps:
* 1.If current node has no children, done.  
* 2.If current node has one children and heap property is broken, 
* 3.Swap the current node and child node and heap down.
* 4.If current node has one children and heap property is broken, find smaller one
* 5.Swap the current node and child node and heap down.
* */
void heapDown(int nodeIndex){
   int leftChildIndex, rightChildIndex, minIndex, tmp;
   leftChildIndex = getLeftChildIndex(nodeIndex);
   rightChildIndex = getRightChildIndex(nodeIndex);
   if (rightChildIndex >= size) {
      if (leftChildIndex >= size)
         return;
      else
         minIndex = leftChildIndex;
   } else {
      if (intArray[leftChildIndex] <= intArray[rightChildIndex])
         minIndex = leftChildIndex;
      else
         minIndex = rightChildIndex;
   }
   if (intArray[nodeIndex] > intArray[minIndex]) {
      tmp = intArray[minIndex];
      intArray[minIndex] = intArray[nodeIndex];
      intArray[nodeIndex] = tmp;
      heapDown(minIndex);
   }
}
void insert(int value) {            
   size++;
   intArray[size - 1] = value;
   heapUp(size - 1);
}
void removeMin() {
   intArray[0] = intArray[size - 1];
   size--;
   if (size > 0)
      heapDown(0);
}
main() {
   /*                     5                //Level 0
   * 
   */
   insert(5);
   /*                     1                //Level 0
   *                     |
   *                 5---|                 //Level 1
   */   
   insert(1);
   /*                     1                //Level 0
   *                     |
   *                 5---|---3             //Level 1
   */
   insert(3);
   /*                     1                //Level 0
   *                     |
   *                 5---|---3             //Level 1
   *                 |
   *              8--|                     //Level 2
   */
   insert(8);
   /*                     1                //Level 0
   *                     |
   *                 5---|---3             //Level 1
   *                 |
   *              8--|--9                  //Level 2
   */
   insert(9);
   /*                     1                 //Level 0
   *                     |
   *                 5---|---3              //Level 1
   *                 |       |
   *              8--|--9 6--|              //Level 2
   */
   insert(6);
   /*                     1                 //Level 0
   *                     |
   *                 5---|---2              //Level 1
   *                 |       | 
   *              8--|--9 6--|--3           //Level 2
   */
   insert(2);

   printf("%d", getMinimum());

   removeMin();
   /*                     2                 //Level 0
   *                     |
   *                 5---|---3              //Level 1
   *                 |       |
   *              8--|--9 6--|              //Level 2
   */
   printf("\n%d", getMinimum());   
}

如果我們編譯並執行上述程式，它將產生以下結果：

1
2
列印頁面
上一頁
下一頁
廣告