一般樹和二叉樹的區別

---

在數學和計算機科學中，樹都是基礎概念。它們幫助我們以有序的方式組織資料，就像家譜圖展示不同家庭成員之間的關係一樣。然而，在技術意義上討論時，樹有幾種型別，每種都有其獨特的特性。二叉樹和一般樹是兩種最常見的型別。如果您是第一次接觸這個主題，請不要擔心！本文將以易於理解的方式解釋這些概念。閱讀完本文後，您將理解一般樹和二叉樹、它們的區別以及它們的應用。

什麼是計算機科學中的樹？

在繼續討論一般樹和二叉樹之前，讓我們首先回顧一下計算機科學中樹的定義。

• 樹：樹是一種特殊的資料結構，類似於倒置的樹。它從根節點（或頂部節點）開始。任何節點都可以連線到其“子節點”或其他節點，從而建立一個分支結構。想象一下家譜圖，其中每個人（節點）都可以有與其相關的後代（其他節點）。
• 節點：在樹中，節點是基本單元。它包含資料以及指向其他節點（或邊）的連結。除了根節點沒有父節點外，每個節點只有一個父節點。
• 邊：邊是兩個節點之間的連線。它表示它們之間的關係，就像連線父母和孩子的線一樣。
• 葉節點：沒有子節點的節點稱為葉節點。它類似於樹枝的尖端。

一般樹

一般樹是一種樹形資料結構，其中每個節點可以具有任意數量的子節點。這意味著一個節點可以是一個、兩個甚至十個子節點的父節點！節點的子節點數量沒有限制。

示例

考慮一個公司的組織結構圖。市場部、銷售部和財務部的副總裁直接向位於組織頂部的執行長彙報。每個副總裁下面可能有其他團隊成員，而這些團隊成員可能又有自己的團隊成員。因此，就形成了一個一般樹。

關鍵點

• 靈活的結構：節點可以有多個子節點，使其成為表示複雜層次結構的多功能結構。
• 用例：一般樹通常用於檔案系統、組織結構和其他複雜的分層資料。

二叉樹

二叉樹：二叉樹是⼀種特殊型別的一般樹，其中每個節點最多可以有兩個子節點。這些子節點通常被稱為左子節點和右子節點。

示例

考慮這樣一個場景：在決策過程中，每個問題都有兩個可能的答案：是或否。後續的決策問題形成了⼀棵二叉樹。

關鍵點

• 嚴格的結構：節點最多隻能有兩個子節點，使其更容易管理和理解。
• 用例：二叉樹經常用於排序、搜尋和決策演算法。

一般樹與二叉樹：比較

現在我們知道了它們是什麼，讓我們並排比較一下一般樹和二叉樹。

方面	一般樹	二叉樹
定義	每個節點可以有任意數量子節點的樹。	每個節點最多可以有兩個子節點的樹。
節點結構	每個節點可以有0到多個子節點。	每個節點可以有0、1或2個子節點（左和右）。
節點度	節點可以擁有的子節點數量沒有限制。	每個節點最多可以有兩個子節點（左和右）。
父子關係	一個節點可以有多個子節點。	一個節點最多可以有兩個子節點（左子節點和右子節點）。
靈活性	高度靈活，可以表示複雜的層次結構。	靈活性較低，每個節點嚴格限制為兩個子節點。
子樹順序	子樹是無序的。	子樹是有序的（左和右）。
空樹	不能為空。	可以為空。
複雜度	由於對子節點數量沒有限制，因此實現和管理起來更復雜。	由於其簡單和受限的結構，因此更容易實現和管理。
用例	用於檔案系統、組織結構圖和一般層次結構。	常用在二叉搜尋樹、決策樹和二叉堆中。
演算法效率	由於潛在的複雜性，通常不用於關注效率的演算法。	對於像搜尋、排序和平衡樹這樣的演算法非常高效。
遍歷方法	由於每個節點的子節點數量不同，因此遍歷方法（例如，先序、後序）更復雜。	標準遍歷方法（中序、先序、後序）定義明確且簡單。
記憶體使用	由於每個節點可能有很多子節點，因此可能會消耗更多記憶體。	由於有兩個子節點的限制，因此通常更節省記憶體。
平衡	由於子節點數量靈活，因此通常難以平衡。	在特殊形式（例如，AVL樹、紅黑樹）中更容易保持平衡。
示例場景	組織結構、分類樹、一般層次結構。	二叉搜尋樹、決策過程、表示式樹。

此表全面概述了一般樹和二叉樹之間的關鍵區別，使您更容易理解哪種樹結構更適合給定的用例。

視覺化表示

一般樹示例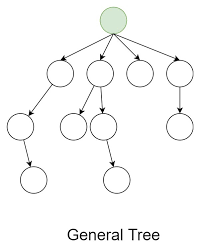

二叉樹示例

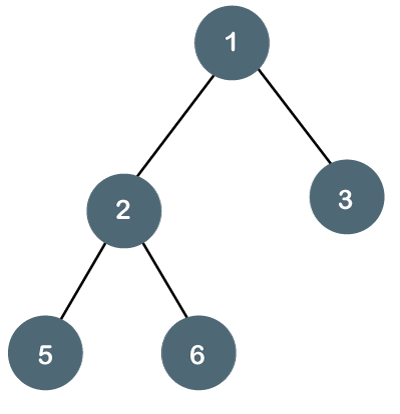
為什麼這些差異很重要？

鑑於一般樹和二叉樹用於不同的環境，理解它們的區別至關重要。

• 複雜的資料結構：對於表示複雜的資料結構（例如檔案系統和組織結構圖），其中節點可能需要連結到多個子節點，一般樹是最佳選擇。
• 高效的搜尋和排序：由於其嚴格的結構加快並提高了這些過程的效率，二叉樹經常用於計算機演算法中進行高效的搜尋和排序。

關於一般樹與二叉樹的常見問題

1. 二叉樹可以被認為是一般樹嗎？

是的，二叉樹是一種一般樹，其限制是每個節點最多隻能有兩個子節點。

2. 為什麼在演算法中更傾向於使用二叉樹？

許多演算法都偏愛二叉樹，因為它的結構使搜尋、排序和決策過程更有效。

3. 除了二叉樹和一般樹之外，還有其他型別的樹嗎？

是的，還有其他型別的樹，例如B樹、紅黑樹和AVL樹，每種都有其獨特的用途。

結論

學習更復雜的資料結構始於理解一般樹和二叉樹之間的區別。儘管一般樹靈活且擅長描述複雜的關係，但二叉樹由於其更高的演算法效率而經常被選擇。無論您是在組織檔案系統中的資料，還是建立搜尋資訊的演算法，瞭解使用哪種型別的樹至關重要。