資料結構
網路
關係型資料庫管理系統
作業系統
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 程式設計
C++
C#
MongoDB
MySQL
Javascript
PHP
物理學
化學
生物學
數學
英語
經濟學
心理學
社會學
時尚研究
法律研究C++ 中二叉樹轉換為二叉搜尋樹
二叉樹是一種特殊的樹，其中樹的每個節點最多可以有兩個子節點。這些子節點稱為右子節點和左子節點。
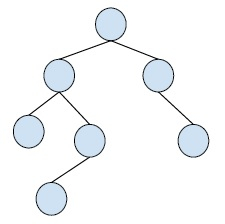
一個簡單的二叉樹是 -
二叉搜尋樹 (BST) 是一種特殊的樹，它遵循以下規則 -
左子節點的值總是小於父節點 注意
右子節點的值大於父節點。
所有節點分別形成一個二叉搜尋樹。
二叉搜尋樹 (BST) 的示例 -
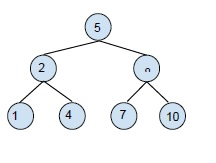
建立二叉搜尋樹是為了降低搜尋、查詢最小值和最大值等操作的複雜度。
在這裡，我們給定一個二叉樹，我們必須將此二叉樹(BT) 轉換為二叉搜尋樹(BST)。在此轉換中，二叉樹的原始結構不應更改。
讓我們舉個例子來理解如何將BT 轉換為 BST -
輸入 -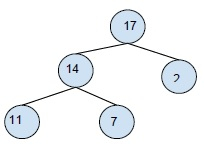
輸出 -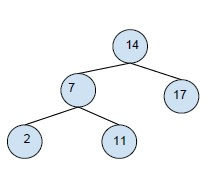
將二叉樹轉換為二叉搜尋樹分三個步驟進行。它們是 -
步驟 1 - 將二叉樹的中序遍歷資料儲存到陣列arr[] 中。
步驟 2 - 使用任何排序技術對陣列 arr[] 進行排序。
步驟 3 - 現在，對樹進行中序遍歷，並將陣列中的元素逐個複製到樹的節點中。
示例
#include<stdio.h>
#include<stdlib.h>
struct node{
int data;
struct node *left;
struct node *right;
};
void Inordertraversal(struct node* node, int inorder[], int *index_ptr){
if (node == NULL)
return;
Inordertraversal(node->left, inorder, index_ptr);
inorder[*index_ptr] = node->data;
(*index_ptr)++;
Inordertraversal(node->right, inorder, index_ptr);
}
int countNodes(struct node* root){
if (root == NULL)
return 0;
return countNodes (root->left) +
countNodes (root->right) + 1;
}
int compare (const void * a, const void * b){
return( *(int*)a - *(int*)b );
}
void arrayToBST (int *arr, struct node* root, int *index_ptr){
if (root == NULL)
return;
arrayToBST (arr, root->left, index_ptr);
root->data = arr[*index_ptr];
(*index_ptr)++;
arrayToBST (arr, root->right, index_ptr);
}
struct node* newNode (int data){
struct node *temp = new struct node;
temp->data = data;
temp->left = NULL;
temp->right = NULL;
return temp;
}
void printInorder (struct node* node){
if (node == NULL)
return;
printInorder (node->left);
printf("%d ", node->data);
printInorder (node->right);
}
int main(){
struct node *root = NULL;
root = newNode(17);
root->left = newNode(14);
root->right = newNode(2);
root->left->left = newNode(11);
root->right->right = newNode(7);
printf("Inorder Traversal of the binary Tree: \n");
printInorder (root);
int n = countNodes(root);
int *arr = new int[n];
int i = 0;
Inordertraversal(root, arr, &i);
qsort(arr, n, sizeof(arr[0]), compare);
i = 0;
arrayToBST (arr, root, &i);
delete [] arr;
printf("\nInorder Traversal of the converted BST: \n");
printInorder (root);
return 0;
}輸出
Inorder Traversal of the binary Tree: 11 14 17 2 7 Inorder Traversal of the converted BST: 2 7 11 14 17
更新於: 2020-07-13
908 次檢視
廣告